library(tidyverse)
library(tidymodels)
tidymodels_prefer()
library(kernlab)
library(mlbench)
library(caret)
library(knitr)
library(ggcorrplot)
library(skimr)
library(GGally)
library(finetune)
library(lubridate)
library(baguette)
library(patchwork)
library(discrim)
library(reticulate)
library(usemodels)
library(doParallel)
library(naivebayes)
theme_set(theme_bw())Bank Marketing
Introduction
The data is sourced from the UCI ML Repository and can be downloaded here. It is related to the direct marketing campaigns of a Portuguese banking institution. The campaigns were based on phone calls. Multiple datasets are provided, however this analysis focuses on the full dataset (bank-addidtional-full.csv), which is also the latest and has the most number of inputs.
Goal
The classification goal is to predict if the client will subscribe (yes/no) a term deposit (variable y).
Data Dictionary
| Attribute Name | Type | Description |
|---|---|---|
| age | numeric | age of the person called |
| job | categorical | type of job |
| marital status | categorical | married, single or unknown |
| education | categorical | educational attainment |
| default | categorical | has credit in default? |
| housing | categorical | has housing loan? |
| loan | categorical | has personal loan? |
| contact | categorical | contact communication type |
| month | categorical | last contact month of year |
| day_of_week | categorical | last contact day of week |
| duration | numeric | last contact duration in seconds. The duration is not known before the call, so even though this has a strong impact on outcome (duration=0 => y=0), it should be discarded from the model |
| campaign | numeric | number of contacts performed during this campaign for this client (includes last contact) |
| pdays | numeric | number of days passed since client was contacted since the client was last contacted from a previous campaign. 999 means not previously contacted |
| previous | numeric | number of contacts performed during this campaign for this client |
| poutcome | categorical | outcome of the previous marketing campaign |
| emp.var.rate | numeric | employment variation rate - quarterly indicator |
| cons.price.idx | numeric | consumer price index - monthly indicator |
| cons.conf.idx | numeric | consumer confidence index - monthly indicator |
| euribor3m | numeric | euribor 3 month rate - daily indicator. These are European interest rates. |
| nr.employed | numeric | number of employees - quarterly indicator |
| y | categorical | has the client subscribed a term deposit? |
Load Packages
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import sklearn.metrics as metrics
import IPython.display as dsp
from IPython.display import HTML
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler, FunctionTransformer, PolynomialFeatures, OneHotEncoder, PowerTransformer, LabelEncoder
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline
from sklearn.pipeline import make_pipeline
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.linear_model import LogisticRegression, LogisticRegressionCV, ElasticNet, SGDClassifier, Perceptron
from sklearn.model_selection import cross_val_score, GridSearchCV, KFold, StratifiedKFold, RandomizedSearchCV
from sklearn.calibration import CalibratedClassifierCV
from sklearn.feature_selection import VarianceThreshold
from sklearn.naive_bayes import GaussianNB
from xgboost import XGBClassifier
sns.set_theme()
import warnings
warnings.filterwarnings('ignore')Load Data
Sample 10 rows
#knitr::kable(as_tibble(head(data_bank_marketing, n=10)))
set.seed(42)
knitr::kable(slice_sample(data_bank_marketing, n=10))| age | job | marital | education | default | housing | loan | contact | month | day_of_week | duration | campaign | pdays | previous | poutcome | emp.var.rate | cons.price.idx | cons.conf.idx | euribor3m | nr.employed | y |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 23 | blue-collar | married | basic.9y | no | yes | no | cellular | may | wed | 52 | 4 | 999 | 0 | nonexistent | -18 | 92893 | -462 | 1.281 | 50991 | no |
| 45 | admin. | married | basic.9y | unknown | yes | no | telephone | jun | thu | 60 | 1 | 999 | 0 | nonexistent | 14 | 94465 | -418 | 4.866 | 52281 | no |
| 41 | technician | single | university.degree | no | no | no | cellular | jul | thu | 537 | 2 | 999 | 0 | nonexistent | 14 | 93918 | -427 | 4.962 | 52281 | no |
| 31 | blue-collar | single | unknown | no | yes | no | telephone | may | fri | 273 | 2 | 999 | 0 | nonexistent | 11 | 93994 | -364 | 4.864 | 5191 | no |
| 36 | technician | single | professional.course | no | no | no | cellular | jun | fri | 146 | 2 | 999 | 0 | nonexistent | -29 | 92963 | -408 | 1.268 | 50762 | yes |
| 50 | blue-collar | married | basic.4y | unknown | yes | yes | telephone | jun | fri | 144 | 15 | 999 | 0 | nonexistent | 14 | 94465 | -418 | 4.967 | 52281 | no |
| 28 | technician | married | basic.9y | no | yes | no | cellular | may | wed | 224 | 1 | 999 | 1 | failure | -18 | 92893 | -462 | 1.281 | 50991 | no |
| 32 | admin. | single | university.degree | no | no | no | cellular | jul | thu | 792 | 1 | 999 | 0 | nonexistent | 14 | 93918 | -427 | 4.963 | 52281 | no |
| 59 | retired | divorced | basic.4y | no | no | yes | cellular | jul | mon | 210 | 3 | 999 | 2 | failure | -17 | 94215 | -403 | 0.827 | 49916 | yes |
| 35 | technician | married | professional.course | no | no | no | cellular | apr | wed | 225 | 2 | 999 | 0 | nonexistent | -18 | 93075 | -471 | 1.415 | 50991 | no |
pd.set_option('display.width', 500)
#pd.set_option('precision', 3)
sample=data_bank_marketing.sample(10)
dsp.Markdown(sample.to_markdown(index=False))| age | job | marital | education | default | housing | loan | contact | month | day_of_week | duration | campaign | pdays | previous | poutcome | emp.var.rate | cons.price.idx | cons.conf.idx | euribor3m | nr.employed | y |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 45 | admin. | single | high.school | no | no | no | telephone | jun | wed | 192 | 6 | 999 | 0 | nonexistent | 1.4 | 94.465 | -41.8 | 4.864 | 5228.1 | no |
| 66 | retired | married | basic.4y | no | yes | yes | telephone | aug | wed | 82 | 3 | 999 | 3 | failure | -2.9 | 92.201 | -31.4 | 0.854 | 5076.2 | no |
| 33 | management | single | university.degree | no | unknown | unknown | cellular | jun | tue | 73 | 1 | 999 | 0 | nonexistent | -2.9 | 92.963 | -40.8 | 1.262 | 5076.2 | no |
| 40 | blue-collar | married | basic.4y | unknown | unknown | unknown | telephone | jul | wed | 135 | 1 | 999 | 0 | nonexistent | 1.4 | 93.918 | -42.7 | 4.962 | 5228.1 | no |
| 43 | services | divorced | professional.course | no | no | no | cellular | may | fri | 196 | 2 | 999 | 0 | nonexistent | -1.8 | 92.893 | -46.2 | 1.313 | 5099.1 | no |
| 36 | blue-collar | married | basic.6y | no | no | no | telephone | may | fri | 189 | 2 | 999 | 0 | nonexistent | 1.1 | 93.994 | -36.4 | 4.857 | 5191 | no |
| 23 | student | single | high.school | no | no | no | cellular | jun | wed | 200 | 2 | 999 | 0 | nonexistent | -2.9 | 92.963 | -40.8 | 1.26 | 5076.2 | yes |
| 27 | technician | single | professional.course | no | no | no | telephone | jun | fri | 112 | 5 | 999 | 0 | nonexistent | 1.4 | 94.465 | -41.8 | 4.967 | 5228.1 | no |
| 32 | technician | married | university.degree | no | yes | no | telephone | jul | wed | 196 | 1 | 999 | 0 | nonexistent | 1.4 | 93.918 | -42.7 | 4.962 | 5228.1 | no |
| 31 | admin. | single | high.school | no | yes | no | cellular | may | thu | 1094 | 2 | 999 | 0 | nonexistent | -1.8 | 92.893 | -46.2 | 1.266 | 5099.1 | yes |
10×21 DataFrame
Row │ age job marital education default housing lo ⋯
│ Int64 String15 String15 String31 String7 String7 St ⋯
─────┼──────────────────────────────────────────────────────────────────────────
1 │ 56 housemaid married basic.4y no no no ⋯
2 │ 57 services married high.school unknown no no
3 │ 37 services married high.school no yes no
4 │ 40 admin. married basic.6y no no no
5 │ 56 services married high.school no no ye ⋯
6 │ 45 services married basic.9y unknown no no
7 │ 59 admin. married professional.course no no no
8 │ 41 blue-collar married unknown unknown no no
9 │ 24 technician single professional.course no yes no ⋯
10 │ 25 services single high.school no yes no
15 columns omitted┌───────┬─────────────┬──────────┬─────────────────────┬─────────┬─────────┬─────────┬───────────┬─────────┬─────────────┬──────────┬──────────┬───────┬──────────┬─────────────┬──────────────┬────────────────┬───────────────┬───────────┬─────────────┬─────────┐
│ age │ job │ marital │ education │ default │ housing │ loan │ contact │ month │ day_of_week │ duration │ campaign │ pdays │ previous │ poutcome │ emp.var.rate │ cons.price.idx │ cons.conf.idx │ euribor3m │ nr.employed │ y │
│ Int64 │ String15 │ String15 │ String31 │ String7 │ String7 │ String7 │ String15 │ String3 │ String3 │ Int64 │ Int64 │ Int64 │ Int64 │ String15 │ Float64 │ Float64 │ Float64 │ Float64 │ Float64 │ String3 │
├───────┼─────────────┼──────────┼─────────────────────┼─────────┼─────────┼─────────┼───────────┼─────────┼─────────────┼──────────┼──────────┼───────┼──────────┼─────────────┼──────────────┼────────────────┼───────────────┼───────────┼─────────────┼─────────┤
│ 56 │ housemaid │ married │ basic.4y │ no │ no │ no │ telephone │ may │ mon │ 261 │ 1 │ 999 │ 0 │ nonexistent │ 1.1 │ 93.994 │ -36.4 │ 4.857 │ 5191.0 │ no │
│ 57 │ services │ married │ high.school │ unknown │ no │ no │ telephone │ may │ mon │ 149 │ 1 │ 999 │ 0 │ nonexistent │ 1.1 │ 93.994 │ -36.4 │ 4.857 │ 5191.0 │ no │
│ 37 │ services │ married │ high.school │ no │ yes │ no │ telephone │ may │ mon │ 226 │ 1 │ 999 │ 0 │ nonexistent │ 1.1 │ 93.994 │ -36.4 │ 4.857 │ 5191.0 │ no │
│ 40 │ admin. │ married │ basic.6y │ no │ no │ no │ telephone │ may │ mon │ 151 │ 1 │ 999 │ 0 │ nonexistent │ 1.1 │ 93.994 │ -36.4 │ 4.857 │ 5191.0 │ no │
│ 56 │ services │ married │ high.school │ no │ no │ yes │ telephone │ may │ mon │ 307 │ 1 │ 999 │ 0 │ nonexistent │ 1.1 │ 93.994 │ -36.4 │ 4.857 │ 5191.0 │ no │
│ 45 │ services │ married │ basic.9y │ unknown │ no │ no │ telephone │ may │ mon │ 198 │ 1 │ 999 │ 0 │ nonexistent │ 1.1 │ 93.994 │ -36.4 │ 4.857 │ 5191.0 │ no │
│ 59 │ admin. │ married │ professional.course │ no │ no │ no │ telephone │ may │ mon │ 139 │ 1 │ 999 │ 0 │ nonexistent │ 1.1 │ 93.994 │ -36.4 │ 4.857 │ 5191.0 │ no │
│ 41 │ blue-collar │ married │ unknown │ unknown │ no │ no │ telephone │ may │ mon │ 217 │ 1 │ 999 │ 0 │ nonexistent │ 1.1 │ 93.994 │ -36.4 │ 4.857 │ 5191.0 │ no │
│ 24 │ technician │ single │ professional.course │ no │ yes │ no │ telephone │ may │ mon │ 380 │ 1 │ 999 │ 0 │ nonexistent │ 1.1 │ 93.994 │ -36.4 │ 4.857 │ 5191.0 │ no │
│ 25 │ services │ single │ high.school │ no │ yes │ no │ telephone │ may │ mon │ 50 │ 1 │ 999 │ 0 │ nonexistent │ 1.1 │ 93.994 │ -36.4 │ 4.857 │ 5191.0 │ no │
└───────┴─────────────┴──────────┴─────────────────────┴─────────┴─────────┴─────────┴───────────┴─────────┴─────────────┴──────────┴──────────┴───────┴──────────┴─────────────┴──────────────┴────────────────┴───────────────┴───────────┴─────────────┴─────────┘10×21 DataFrame
Row │ age job marital education default housing loan contact month day_of_week duration campaign pdays previous poutcome emp.var.rate cons.price.idx cons.conf.idx euribor3m nr.employed y
│ Int64 String15 String15 String31 String7 String7 String7 String15 String3 String3 Int64 Int64 Int64 Int64 String15 Float64 Float64 Float64 Float64 Float64 String3
─────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
1 │ 56 housemaid married basic.4y no no no telephone may mon 261 1 999 0 nonexistent 1.1 93.994 -36.4 4.857 5191.0 no
2 │ 57 services married high.school unknown no no telephone may mon 149 1 999 0 nonexistent 1.1 93.994 -36.4 4.857 5191.0 no
3 │ 37 services married high.school no yes no telephone may mon 226 1 999 0 nonexistent 1.1 93.994 -36.4 4.857 5191.0 no
4 │ 40 admin. married basic.6y no no no telephone may mon 151 1 999 0 nonexistent 1.1 93.994 -36.4 4.857 5191.0 no
5 │ 56 services married high.school no no yes telephone may mon 307 1 999 0 nonexistent 1.1 93.994 -36.4 4.857 5191.0 no
6 │ 45 services married basic.9y unknown no no telephone may mon 198 1 999 0 nonexistent 1.1 93.994 -36.4 4.857 5191.0 no
7 │ 59 admin. married professional.course no no no telephone may mon 139 1 999 0 nonexistent 1.1 93.994 -36.4 4.857 5191.0 no
8 │ 41 blue-collar married unknown unknown no no telephone may mon 217 1 999 0 nonexistent 1.1 93.994 -36.4 4.857 5191.0 no
9 │ 24 technician single professional.course no yes no telephone may mon 380 1 999 0 nonexistent 1.1 93.994 -36.4 4.857 5191.0 no
10 │ 25 services single high.school no yes no telephone may mon 50 1 999 0 nonexistent 1.1 93.994 -36.4 4.857 5191.0 no| Name | data_bank_marketing |
| Number of rows | 41188 |
| Number of columns | 21 |
| _______________________ | |
| Column type frequency: | |
| character | 12 |
| numeric | 9 |
| ________________________ | |
| Group variables | None |
Variable type: character
| skim_variable | n_missing | complete_rate | min | max | empty | n_unique | whitespace |
|---|---|---|---|---|---|---|---|
| job | 0 | 1 | 6 | 13 | 0 | 12 | 0 |
| marital | 0 | 1 | 6 | 8 | 0 | 4 | 0 |
| education | 0 | 1 | 7 | 19 | 0 | 8 | 0 |
| default | 0 | 1 | 2 | 7 | 0 | 3 | 0 |
| housing | 0 | 1 | 2 | 7 | 0 | 3 | 0 |
| loan | 0 | 1 | 2 | 7 | 0 | 3 | 0 |
| contact | 0 | 1 | 8 | 9 | 0 | 2 | 0 |
| month | 0 | 1 | 3 | 3 | 0 | 10 | 0 |
| day_of_week | 0 | 1 | 3 | 3 | 0 | 5 | 0 |
| poutcome | 0 | 1 | 7 | 11 | 0 | 3 | 0 |
| euribor3m | 0 | 1 | 1 | 5 | 0 | 316 | 0 |
| y | 0 | 1 | 2 | 3 | 0 | 2 | 0 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| age | 0 | 1 | 40.02 | 10.42 | 17 | 32 | 38 | 47 | 98 | ▅▇▃▁▁ |
| duration | 0 | 1 | 258.29 | 259.28 | 0 | 102 | 180 | 319 | 4918 | ▇▁▁▁▁ |
| campaign | 0 | 1 | 2.57 | 2.77 | 1 | 1 | 2 | 3 | 56 | ▇▁▁▁▁ |
| pdays | 0 | 1 | 962.48 | 186.91 | 0 | 999 | 999 | 999 | 999 | ▁▁▁▁▇ |
| previous | 0 | 1 | 0.17 | 0.49 | 0 | 0 | 0 | 0 | 7 | ▇▁▁▁▁ |
| emp.var.rate | 0 | 1 | 0.93 | 15.58 | -34 | -18 | 11 | 14 | 14 | ▁▃▁▁▇ |
| cons.price.idx | 0 | 1 | 85475.22 | 26234.18 | 932 | 92893 | 93749 | 93994 | 94767 | ▁▁▁▁▇ |
| cons.conf.idx | 0 | 1 | -365.67 | 119.10 | -508 | -427 | -403 | -361 | -33 | ▇▆▁▁▂ |
| nr.employed | 0 | 1 | 42864.89 | 18170.20 | 5191 | 50175 | 50991 | 52281 | 52281 | ▂▁▁▁▇ |
age duration campaign pdays previous emp.var.rate cons.price.idx cons.conf.idx euribor3m nr.employed
count 41188.00000 41188.000000 41188.000000 41188.000000 41188.000000 41188.000000 41188.000000 41188.000000 41188.000000 41188.000000
mean 40.02406 258.285010 2.567593 962.475454 0.172963 0.081886 93.575664 -40.502600 3.621291 5167.035911
std 10.42125 259.279249 2.770014 186.910907 0.494901 1.570960 0.578840 4.628198 1.734447 72.251528
min 17.00000 0.000000 1.000000 0.000000 0.000000 -3.400000 92.201000 -50.800000 0.634000 4963.600000
25% 32.00000 102.000000 1.000000 999.000000 0.000000 -1.800000 93.075000 -42.700000 1.344000 5099.100000
50% 38.00000 180.000000 2.000000 999.000000 0.000000 1.100000 93.749000 -41.800000 4.857000 5191.000000
75% 47.00000 319.000000 3.000000 999.000000 0.000000 1.400000 93.994000 -36.400000 4.961000 5228.100000
max 98.00000 4918.000000 56.000000 999.000000 7.000000 1.400000 94.767000 -26.900000 5.045000 5228.100000<class 'pandas.core.frame.DataFrame'>
RangeIndex: 41188 entries, 0 to 41187
Data columns (total 21 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 age 41188 non-null int64
1 job 41188 non-null object
2 marital 41188 non-null object
3 education 41188 non-null object
4 default 41188 non-null object
5 housing 41188 non-null object
6 loan 41188 non-null object
7 contact 41188 non-null object
8 month 41188 non-null object
9 day_of_week 41188 non-null object
10 duration 41188 non-null int64
11 campaign 41188 non-null int64
12 pdays 41188 non-null int64
13 previous 41188 non-null int64
14 poutcome 41188 non-null object
15 emp.var.rate 41188 non-null float64
16 cons.price.idx 41188 non-null float64
17 cons.conf.idx 41188 non-null float64
18 euribor3m 41188 non-null float64
19 nr.employed 41188 non-null float64
20 y 41188 non-null object
dtypes: float64(5), int64(5), object(11)
memory usage: 6.6+ MB21×7 DataFrame
Row │ variable mean min median max nmissing eltype
│ Symbol Union… Any Union… Any Int64 DataType
─────┼────────────────────────────────────────────────────────────────────────────
1 │ age 40.0241 17 38.0 98 0 Int64
2 │ job admin. unknown 0 String15
3 │ marital divorced unknown 0 String15
4 │ education basic.4y unknown 0 String31
5 │ default no yes 0 String7
6 │ housing no yes 0 String7
7 │ loan no yes 0 String7
8 │ contact cellular telephone 0 String15
9 │ month apr sep 0 String3
10 │ day_of_week fri wed 0 String3
11 │ duration 258.285 0 180.0 4918 0 Int64
12 │ campaign 2.56759 1 2.0 56 0 Int64
13 │ pdays 962.475 0 999.0 999 0 Int64
14 │ previous 0.172963 0 0.0 7 0 Int64
15 │ poutcome failure success 0 String15
16 │ emp.var.rate 0.0818855 -3.4 1.1 1.4 0 Float64
17 │ cons.price.idx 93.5757 92.201 93.749 94.767 0 Float64
18 │ cons.conf.idx -40.5026 -50.8 -41.8 -26.9 0 Float64
19 │ euribor3m 3.62129 0.634 4.857 5.045 0 Float64
20 │ nr.employed 5167.04 4963.6 5191.0 5228.1 0 Float64
21 │ y no yes 0 String321×3 DataFrame
Row │ names scitypes types
│ Symbol DataType DataType
─────┼──────────────────────────────────────
1 │ age Count Int64
2 │ job Textual String15
3 │ marital Textual String15
4 │ education Textual String31
5 │ default Textual String7
6 │ housing Textual String7
7 │ loan Textual String7
8 │ contact Textual String15
9 │ month Textual String3
10 │ day_of_week Textual String3
11 │ duration Count Int64
12 │ campaign Count Int64
13 │ pdays Count Int64
14 │ previous Count Int64
15 │ poutcome Textual String15
16 │ emp.var.rate Continuous Float64
17 │ cons.price.idx Continuous Float64
18 │ cons.conf.idx Continuous Float64
19 │ euribor3m Continuous Float64
20 │ nr.employed Continuous Float64
21 │ y Textual String3Observations
Only in R, euribor3m is listed as a categorical attribute with 316 unique values, but the data dictionary defines it as numeric.
There are no missing values.
Most of the numeric attributes appear to be left or right skewed.
Most attributes have a high standard deviation.
data_numeric = data_bank_marketing %>% select(-c("job","marital","education","default","housing","loan","contact","month","day_of_week","poutcome","euribor3m","y"))
skew = moments::skewness(data_numeric)
knitr::kable(tidy(skew) %>% arrange(desc(abs(x) )))| names | x |
|---|---|
| pdays | -4.9220107 |
| campaign | 4.7623333 |
| previous | 3.8319027 |
| duration | 3.2630224 |
| cons.price.idx | -2.9107277 |
| cons.conf.idx | 1.9359724 |
| nr.employed | -1.5872345 |
| age | 0.7846682 |
| emp.var.rate | -0.7311321 |
skew = data_bank_marketing.select_dtypes(include=np.number).skew()
dsp.Markdown(skew.to_markdown(index=True))
#print(skew)| 0 | |
|---|---|
| age | 0.784697 |
| duration | 3.26314 |
| campaign | 4.76251 |
| pdays | -4.92219 |
| previous | 3.83204 |
| emp.var.rate | -0.724096 |
| cons.price.idx | -0.230888 |
| cons.conf.idx | 0.30318 |
| euribor3m | -0.709188 |
| nr.employed | -1.04426 |
function skewness_df(df::DataFrame)
numeric_cols = names(df, Real)
m=Matrix(data[!,numeric_cols])
sk=mapslices(skewness,m; dims=1)
sk=reshape(sk, (length(numeric_cols),1))
return hcat(numeric_cols,sk)
endskewness_df (generic function with 1 method)10×2 Matrix{Any}:
"age" 0.784668
"duration" 3.26302
"campaign" 4.76233
"pdays" -4.92201
"previous" 3.8319
"emp.var.rate" -0.724069
"cons.price.idx" -0.230879
"cons.conf.idx" 0.303169
"euribor3m" -0.709162
"nr.employed" -1.04422Observations
- Most attributes have high skewness values.
| age | duration | campaign | pdays | previous | emp.var.rate | cons.price.idx | cons.conf.idx | nr.employed | |
|---|---|---|---|---|---|---|---|---|---|
| age | 1.0000000 | -0.0008657 | 0.0045936 | -0.0343690 | 0.0243647 | 0.0048933 | -0.0194012 | 0.0803944 | -0.0148194 |
| duration | -0.0008657 | 1.0000000 | -0.0716992 | -0.0475770 | 0.0206404 | -0.0253914 | 0.0204889 | -0.0180911 | -0.0145367 |
| campaign | 0.0045936 | -0.0716992 | 1.0000000 | 0.0525836 | -0.0791415 | 0.1510747 | 0.0759259 | -0.0769437 | 0.0153579 |
| pdays | -0.0343690 | -0.0475770 | 0.0525836 | 1.0000000 | -0.5875139 | 0.2643170 | -0.0426908 | -0.0347775 | -0.0798846 |
| previous | 0.0243647 | 0.0206404 | -0.0791415 | -0.5875139 | 1.0000000 | -0.4169615 | -0.0230420 | 0.0385344 | 0.1494358 |
| emp.var.rate | 0.0048933 | -0.0253914 | 0.1510747 | 0.2643170 | -0.4169615 | 1.0000000 | 0.0552787 | -0.0061387 | -0.2773105 |
| cons.price.idx | -0.0194012 | 0.0204889 | 0.0759259 | -0.0426908 | -0.0230420 | 0.0552787 | 1.0000000 | -0.8435170 | -0.1617969 |
| cons.conf.idx | 0.0803944 | -0.0180911 | -0.0769437 | -0.0347775 | 0.0385344 | -0.0061387 | -0.8435170 | 1.0000000 | -0.0039613 |
| nr.employed | -0.0148194 | -0.0145367 | 0.0153579 | -0.0798846 | 0.1494358 | -0.2773105 | -0.1617969 | -0.0039613 | 1.0000000 |
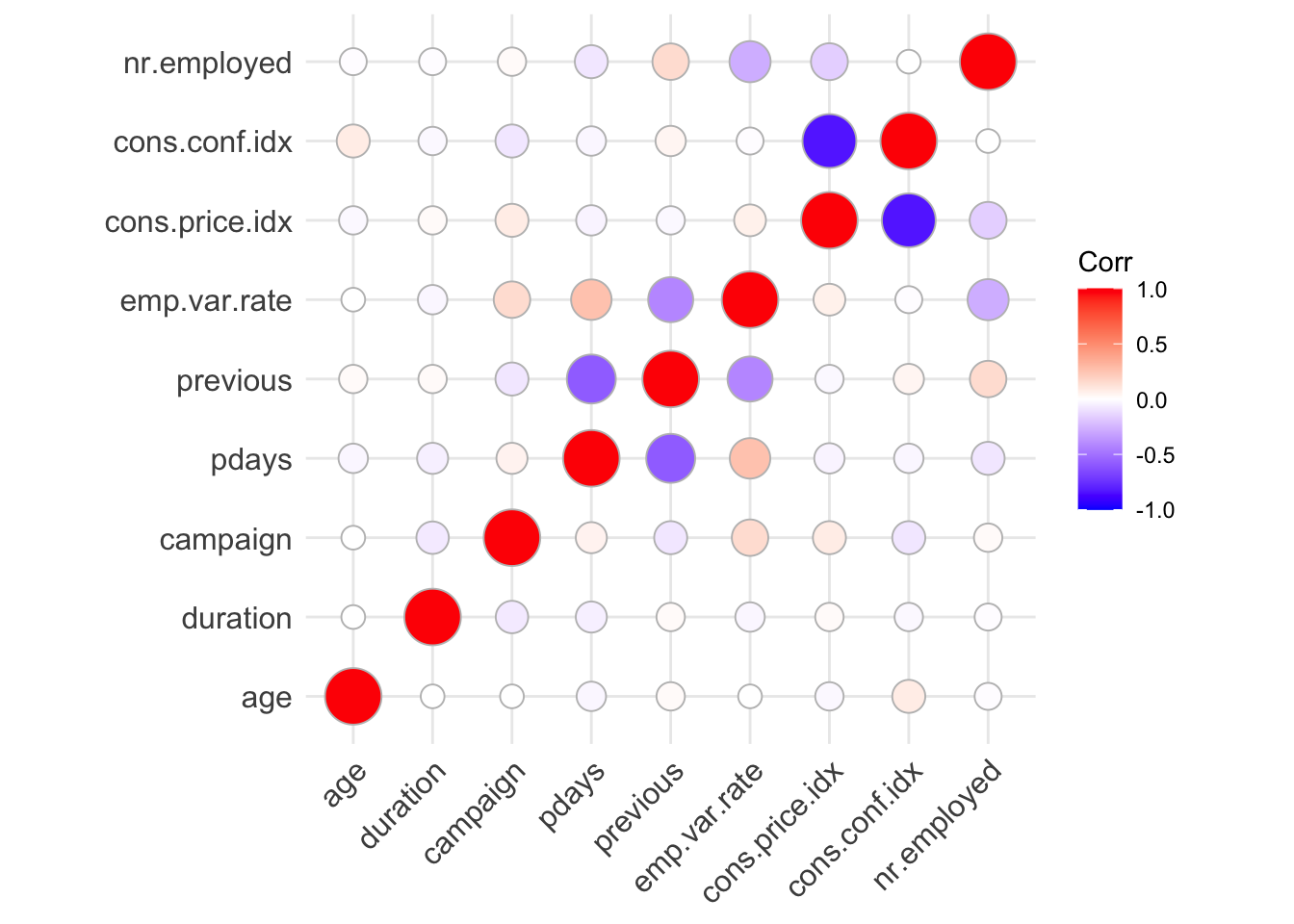
correlations = data_bank_marketing.select_dtypes(include=np.number).corr(method='pearson')
with pd.option_context('display.max_columns', 40):
print(correlations) age duration campaign pdays previous emp.var.rate cons.price.idx cons.conf.idx euribor3m nr.employed
age 1.000000 -0.000866 0.004594 -0.034369 0.024365 -0.000371 0.000857 0.129372 0.010767 -0.017725
duration -0.000866 1.000000 -0.071699 -0.047577 0.020640 -0.027968 0.005312 -0.008173 -0.032897 -0.044703
campaign 0.004594 -0.071699 1.000000 0.052584 -0.079141 0.150754 0.127836 -0.013733 0.135133 0.144095
pdays -0.034369 -0.047577 0.052584 1.000000 -0.587514 0.271004 0.078889 -0.091342 0.296899 0.372605
previous 0.024365 0.020640 -0.079141 -0.587514 1.000000 -0.420489 -0.203130 -0.050936 -0.454494 -0.501333
emp.var.rate -0.000371 -0.027968 0.150754 0.271004 -0.420489 1.000000 0.775334 0.196041 0.972245 0.906970
cons.price.idx 0.000857 0.005312 0.127836 0.078889 -0.203130 0.775334 1.000000 0.058986 0.688230 0.522034
cons.conf.idx 0.129372 -0.008173 -0.013733 -0.091342 -0.050936 0.196041 0.058986 1.000000 0.277686 0.100513
euribor3m 0.010767 -0.032897 0.135133 0.296899 -0.454494 0.972245 0.688230 0.277686 1.000000 0.945154
nr.employed -0.017725 -0.044703 0.144095 0.372605 -0.501333 0.906970 0.522034 0.100513 0.945154 1.000000names = data_bank_marketing.select_dtypes(include=np.number).columns.values.tolist()
hmap=sns.heatmap(correlations,
xticklabels=correlations.columns,
yticklabels=correlations.columns)
hmap.xaxis.tick_top()
plt.xticks(rotation=30)(array([0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5, 9.5]), [Text(0.5, 1, 'age'), Text(1.5, 1, 'duration'), Text(2.5, 1, 'campaign'), Text(3.5, 1, 'pdays'), Text(4.5, 1, 'previous'), Text(5.5, 1, 'emp.var.rate'), Text(6.5, 1, 'cons.price.idx'), Text(7.5, 1, 'cons.conf.idx'), Text(8.5, 1, 'euribor3m'), Text(9.5, 1, 'nr.employed')])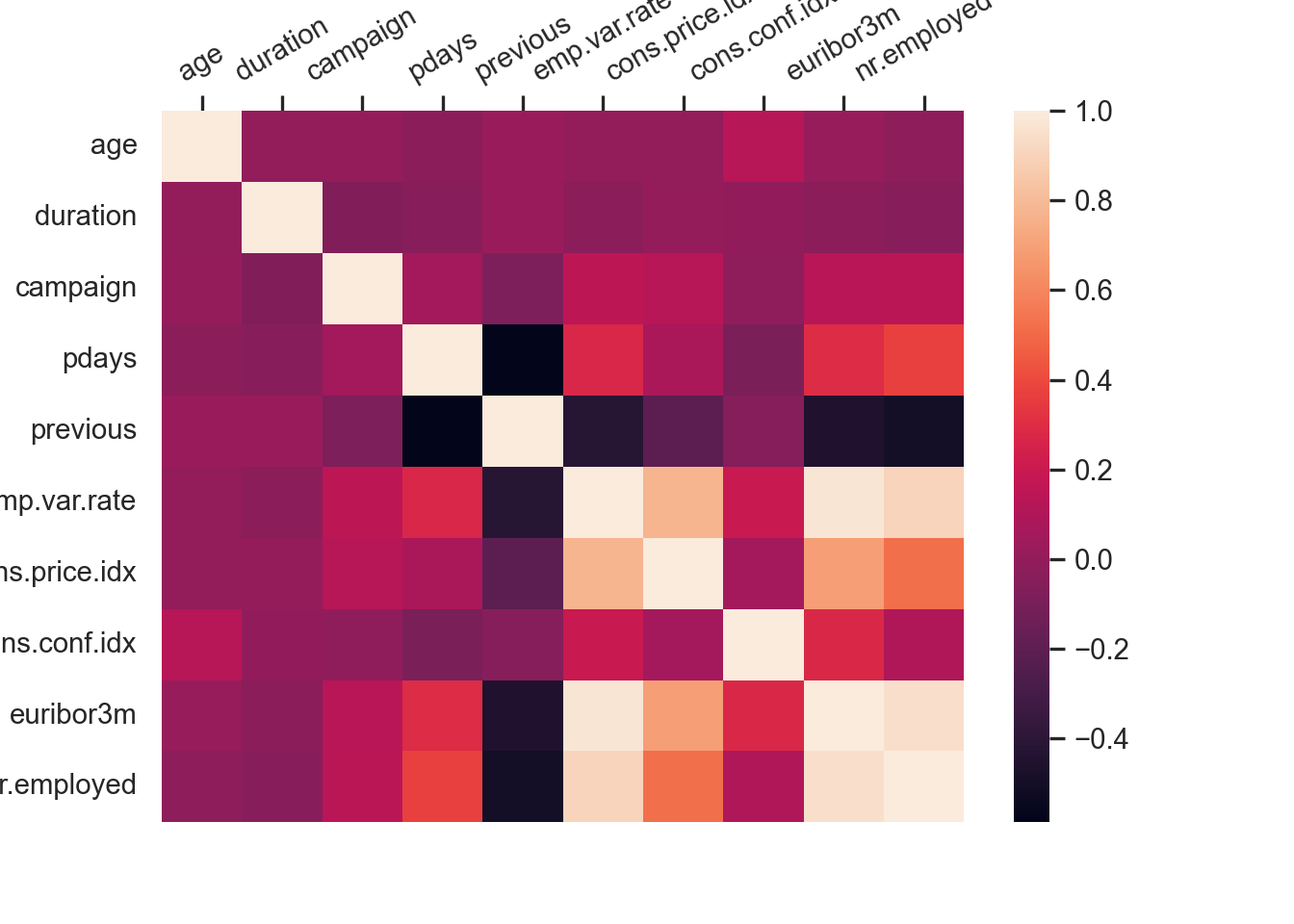
function cor_df(df::DataFrame)
numeric_cols = names(df, Real)
M=Matrix(data[!,numeric_cols])
C=cor(M)
cols=reshape(numeric_cols, 1, (length(numeric_cols)))
(n,m) = size(C)
hm=heatmap(C, fc=cgrad([:white,:dodgerblue4]), xticks=(1:m,numeric_cols), xrot=90, yticks=(1:m,numeric_cols), yflip=true, show = true)
annotate!([(j, i, text(round(C[i,j],digits=3), 8,"Computer Modern",:black)) for i in 1:n for j in 1:m])
return (hm, DataFrame(vcat(cols,C), :auto))
endcor_df (generic function with 1 method)(Plot{Plots.GRBackend() n=1}, 11×10 DataFrame
Row │ x1 x2 x3 x4 x5 x6 ⋯
│ Any Any Any Any Any Any ⋯
─────┼──────────────────────────────────────────────────────────────────────────
1 │ age duration campaign pdays previous emp.var ⋯
2 │ 1.0 -0.000865705 0.00459358 -0.034369 0.0243647 -0.0003
3 │ -0.000865705 1.0 -0.0716992 -0.047577 0.0206404 -0.0279
4 │ 0.00459358 -0.0716992 1.0 0.0525836 -0.0791415 0.15075
5 │ -0.034369 -0.047577 0.0525836 1.0 -0.587514 0.27100 ⋯
6 │ 0.0243647 0.0206404 -0.0791415 -0.587514 1.0 -0.4204
7 │ -0.000370685 -0.0279679 0.150754 0.271004 -0.420489 1.0
8 │ 0.000856715 0.00531227 0.127836 0.0788891 -0.20313 0.77533
9 │ 0.129372 -0.00817287 -0.0137331 -0.0913424 -0.0509364 0.19604 ⋯
10 │ 0.0107674 -0.0328967 0.135133 0.296899 -0.454494 0.97224
11 │ -0.0177251 -0.0447032 0.144095 0.372605 -0.501333 0.90697
5 columns omitted)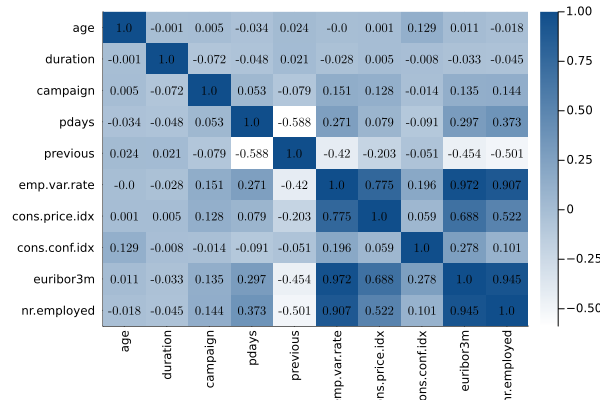
Observations
- There is a negative correlation between cons.conf.idx and cons.price.idx
#https://stackoverflow.com/questions/24901061/in-r-how-do-i-compute-factors-percentage-given-on-different-variable
get_proportions = function(data, attribute, outcome, asPercent = TRUE) {
multiplier = 1
if (asPercent) {
multiplier = 100
}
prop_df = rownames_to_column(multiplier*as.data.frame.matrix(prop.table(table(data %>% select(attribute,outcome)), 1))) %>% as_tibble() #%>% rename(attribute = rowname) %>% as_tibble()
freq_df = as_tibble(multiplier*prop.table(table(data %>% select(attribute))))
final_df = left_join(prop_df, freq_df, by = c(rowname = attribute))
}
knitr::kable(get_proportions(data_bank_marketing, 'job', 'y') %>% rename(job = rowname) %>% rename(overall = n) %>% arrange(desc(yes)))| job | no | yes | overall |
|---|---|---|---|
| student | 68.57143 | 31.428571 | 2.1244052 |
| retired | 74.76744 | 25.232558 | 4.1759736 |
| unemployed | 85.79882 | 14.201183 | 2.4618821 |
| admin. | 87.02744 | 12.972558 | 25.3034865 |
| management | 88.78249 | 11.217510 | 7.0991551 |
| unknown | 88.78788 | 11.212121 | 0.8012042 |
| technician | 89.17396 | 10.826042 | 16.3712732 |
| self-employed | 89.51443 | 10.485573 | 3.4500340 |
| housemaid | 90.00000 | 10.000000 | 2.5735651 |
| entrepreneur | 91.48352 | 8.516483 | 3.5350102 |
| services | 91.86193 | 8.138070 | 9.6363018 |
| blue-collar | 93.10568 | 6.894316 | 22.4677090 |
knitr::kable(get_proportions(data_bank_marketing, 'education', 'y') %>% rename(education = rowname) %>% rename(overall = n) %>% arrange(desc(yes)))| education | no | yes | overall |
|---|---|---|---|
| illiterate | 77.77778 | 22.222222 | 0.043702 |
| unknown | 85.49971 | 14.500289 | 4.202680 |
| university.degree | 86.27548 | 13.724523 | 29.542585 |
| professional.course | 88.65154 | 11.348465 | 12.729436 |
| high.school | 89.16448 | 10.835523 | 23.101389 |
| basic.4y | 89.75096 | 10.249042 | 10.138875 |
| basic.6y | 91.79756 | 8.202443 | 5.564728 |
| basic.9y | 92.17535 | 7.824649 | 14.676605 |
knitr::kable(get_proportions(data_bank_marketing, 'marital', 'y') %>% rename(marital = rowname) %>% rename(overall = n) %>% arrange(desc(yes)))| marital | no | yes | overall |
|---|---|---|---|
| unknown | 85.00000 | 15.00000 | 0.1942313 |
| single | 85.99585 | 14.00415 | 28.0858502 |
| divorced | 89.67910 | 10.32090 | 11.1974361 |
| married | 89.84275 | 10.15725 | 60.5224823 |
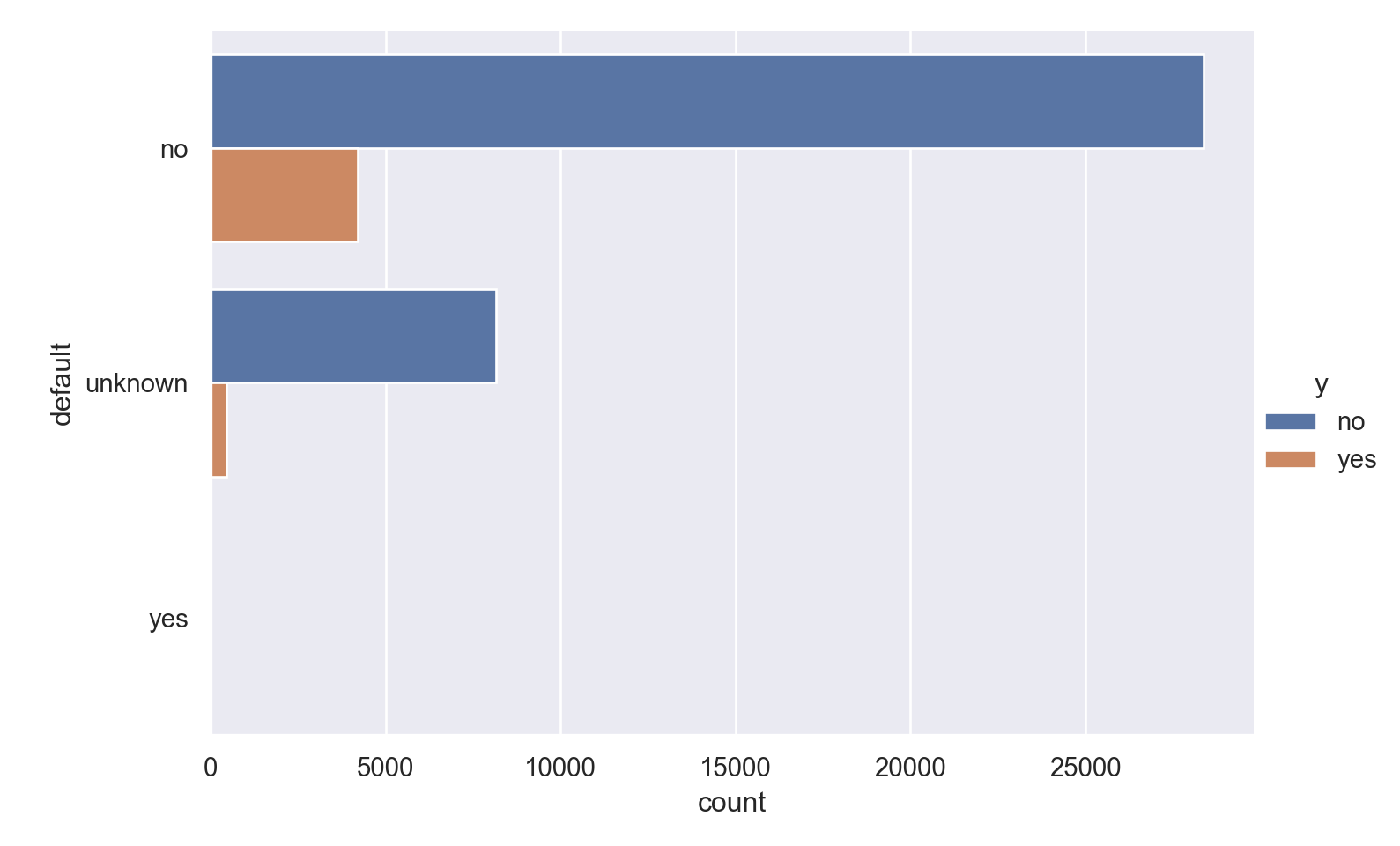
knitr::kable(get_proportions(data_bank_marketing, 'default', 'y') %>% rename(default = rowname) %>% rename(overall = n) %>% arrange(desc(yes)))| default | no | yes | overall |
|---|---|---|---|
| no | 87.12103 | 12.87897 | 79.1201321 |
| unknown | 94.84704 | 5.15296 | 20.8725842 |
| yes | 100.00000 | 0.00000 | 0.0072837 |
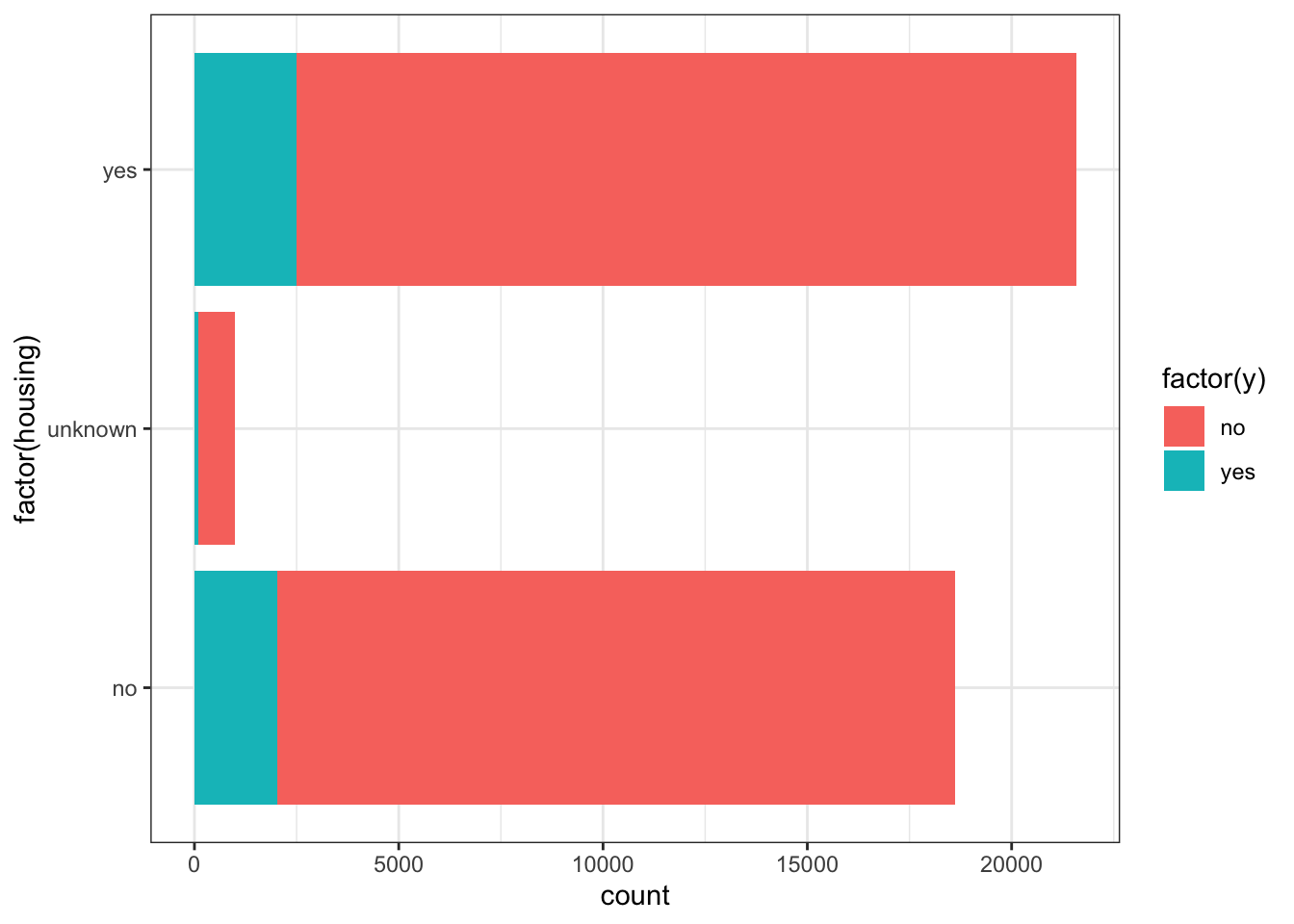
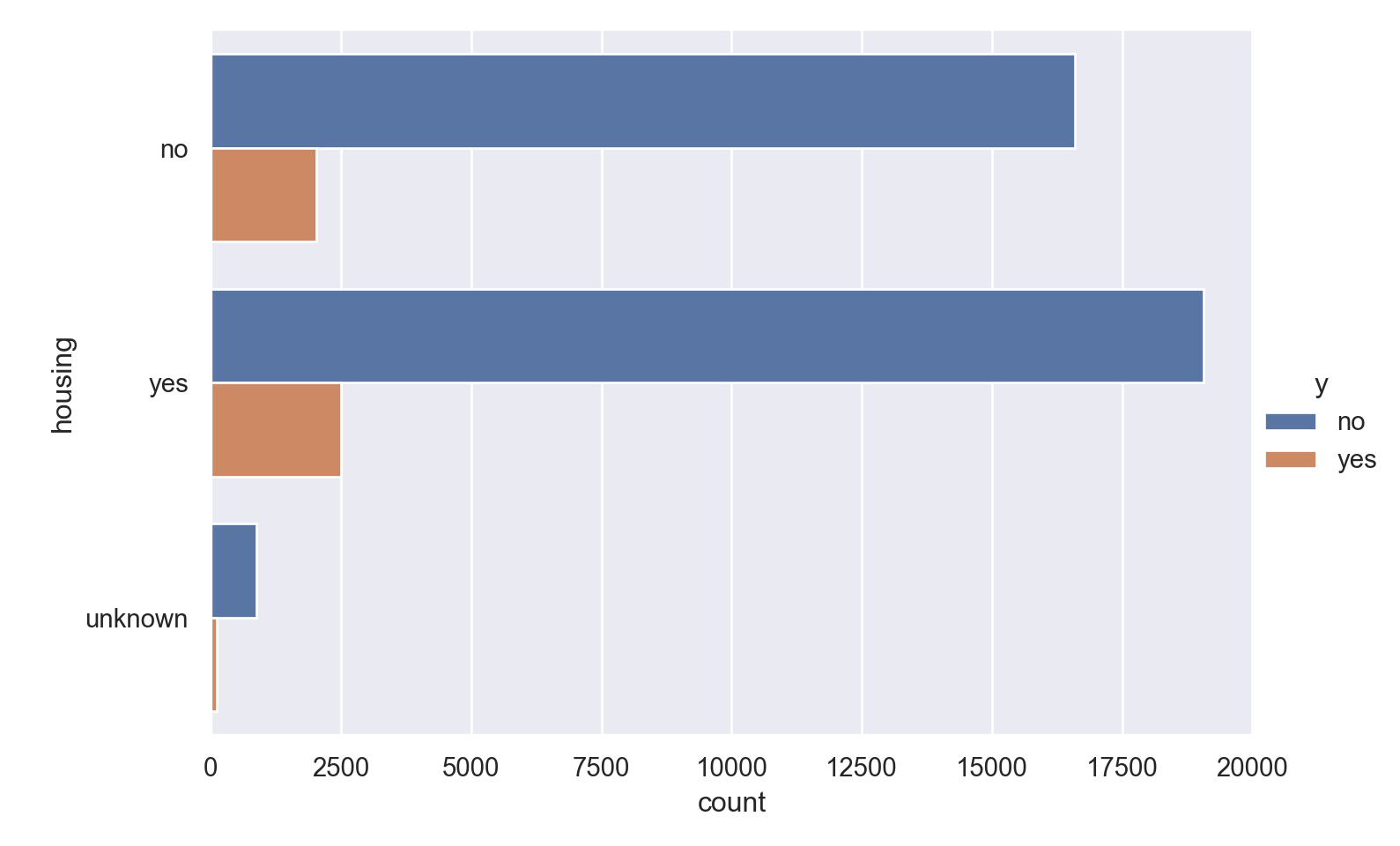
knitr::kable(get_proportions(data_bank_marketing, 'housing', 'y') %>% rename(housing = rowname) %>% rename(overall = n) %>% arrange(desc(yes)))| housing | no | yes | overall |
|---|---|---|---|
| yes | 88.38061 | 11.61939 | 52.384190 |
| no | 89.12040 | 10.87960 | 45.212198 |
| unknown | 89.19192 | 10.80808 | 2.403613 |
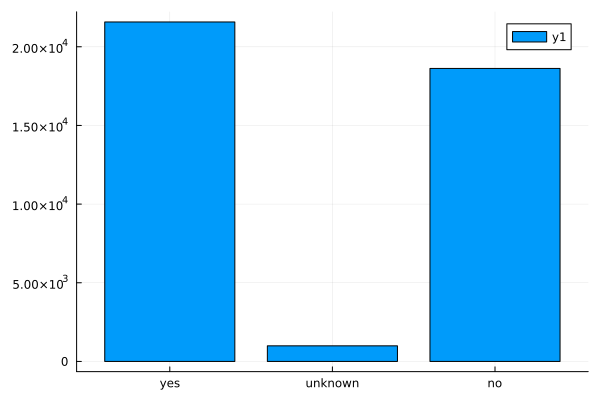
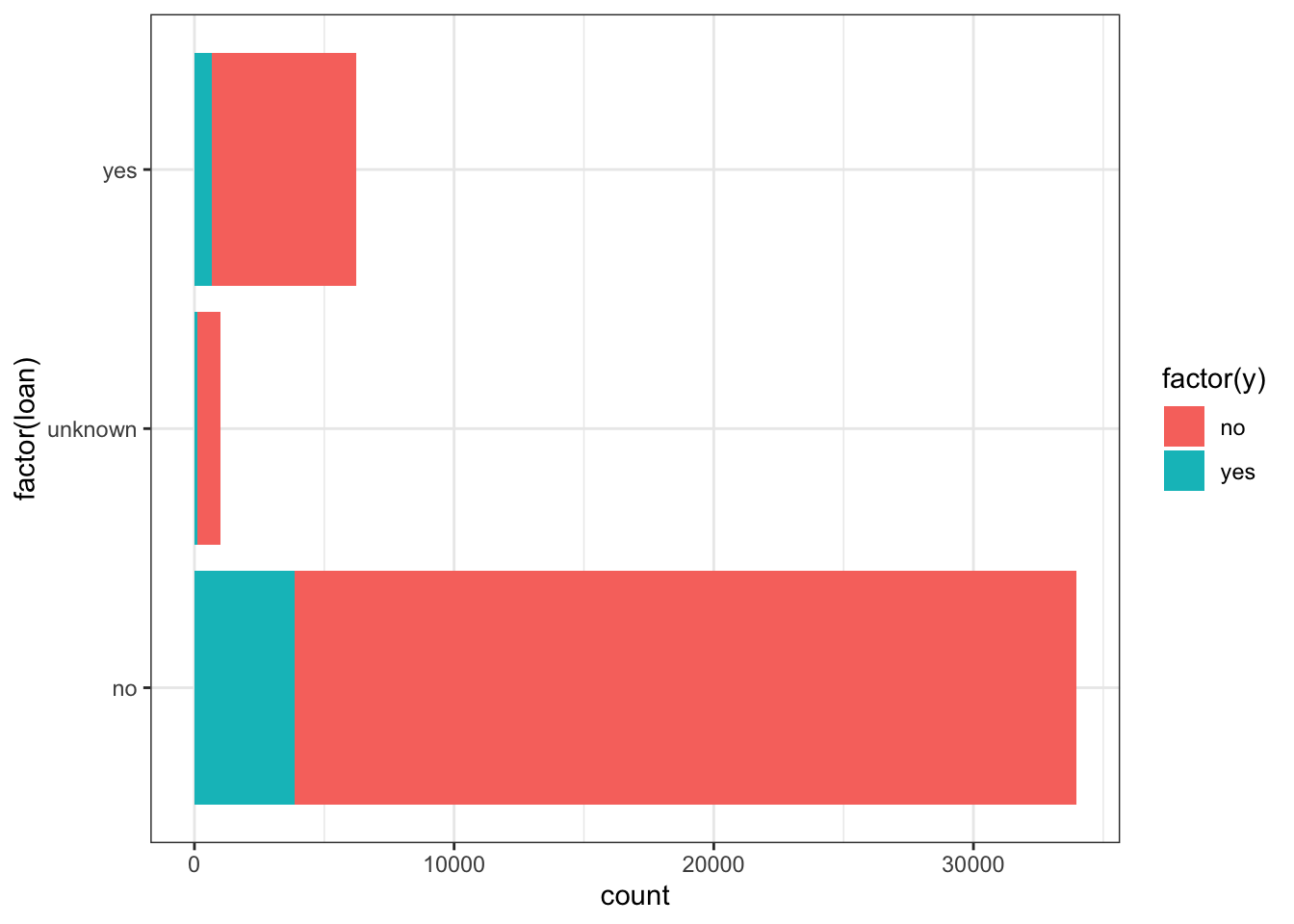
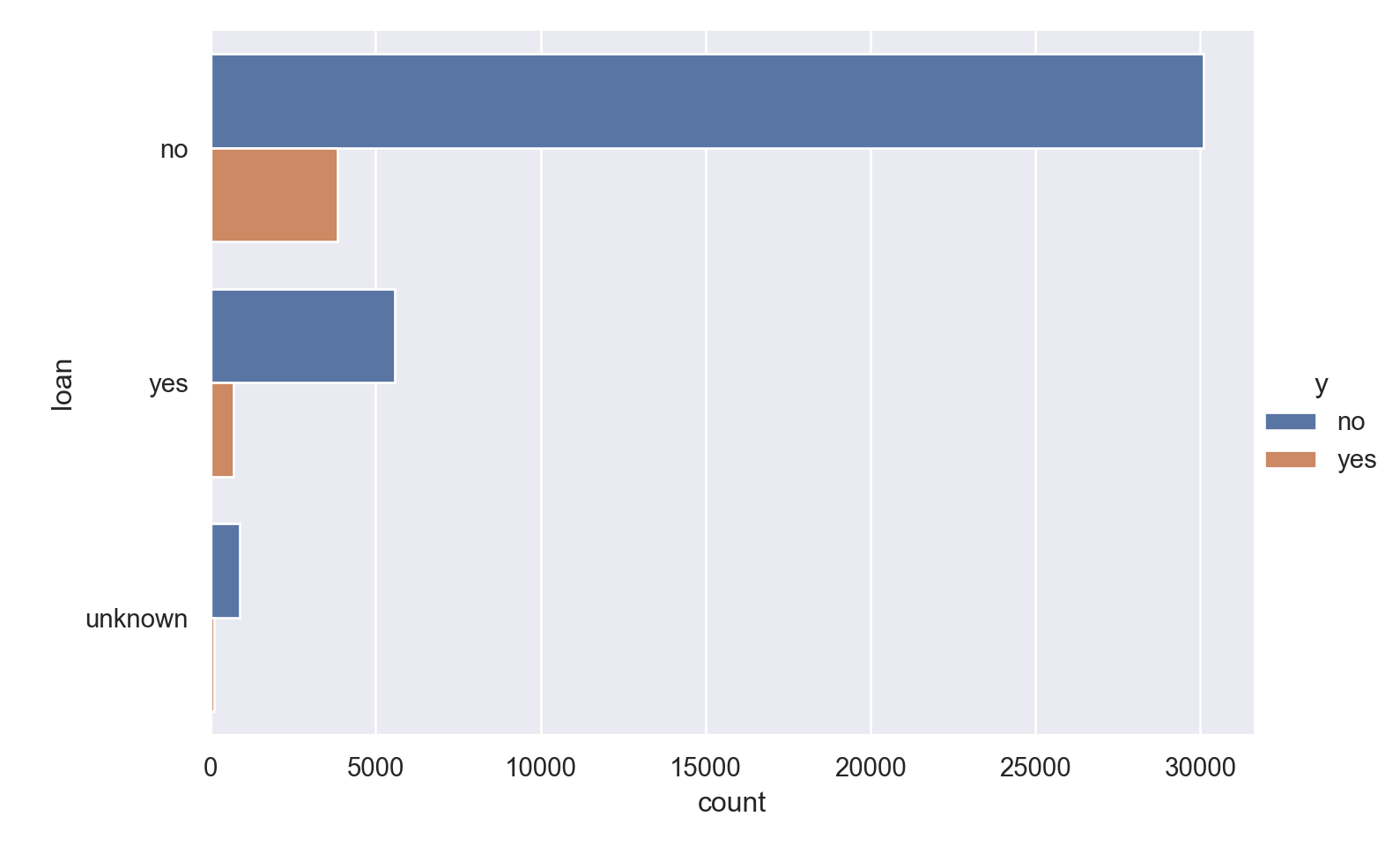
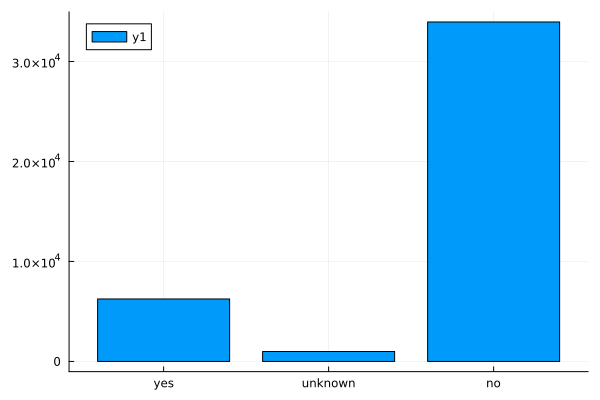
knitr::kable(get_proportions(data_bank_marketing, 'loan', 'y') %>% rename(loan = rowname) %>% rename(overall = n) %>% arrange(desc(yes)))| loan | no | yes | overall |
|---|---|---|---|
| no | 88.65979 | 11.34021 | 82.426920 |
| yes | 89.06850 | 10.93150 | 15.169467 |
| unknown | 89.19192 | 10.80808 | 2.403613 |
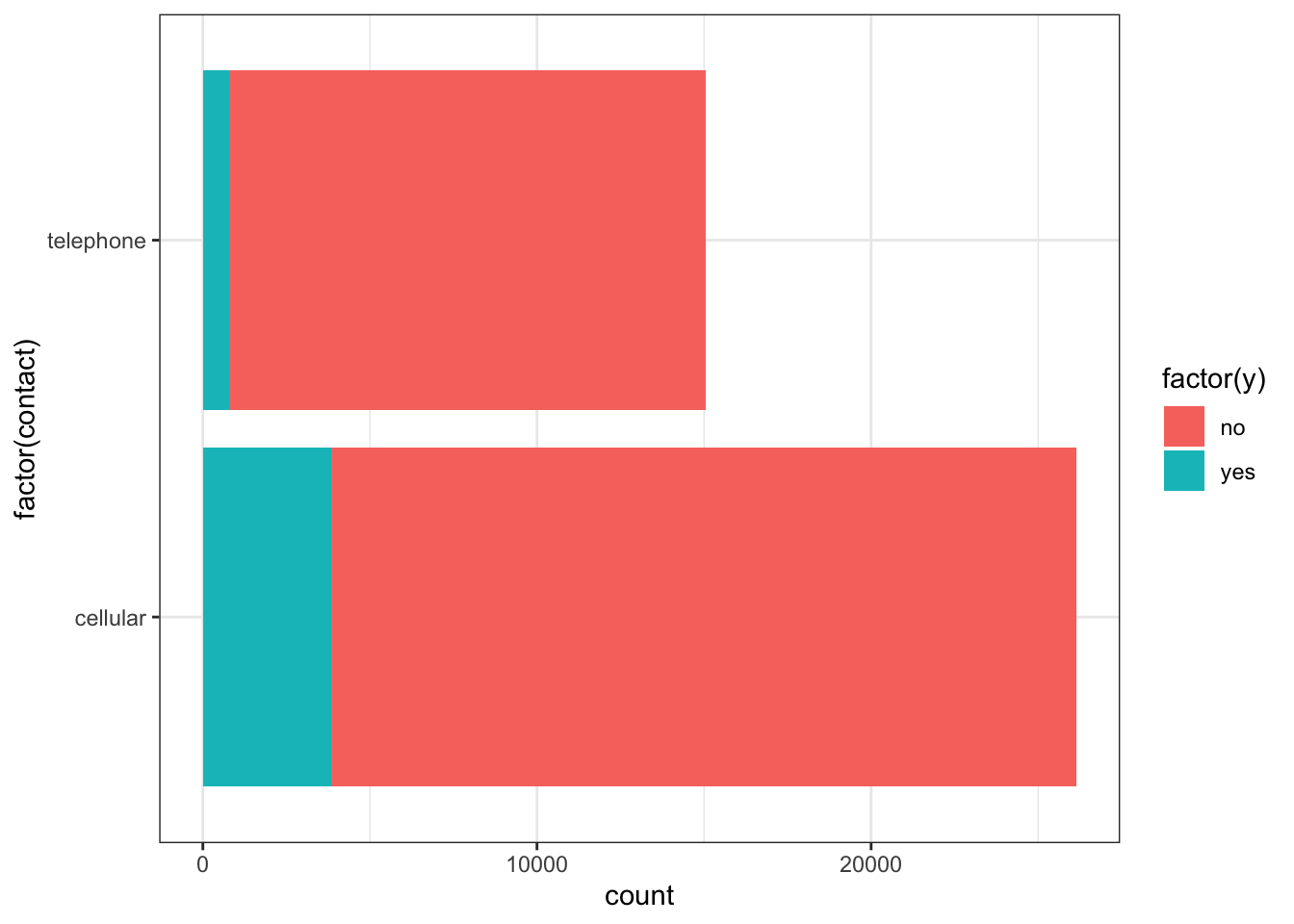
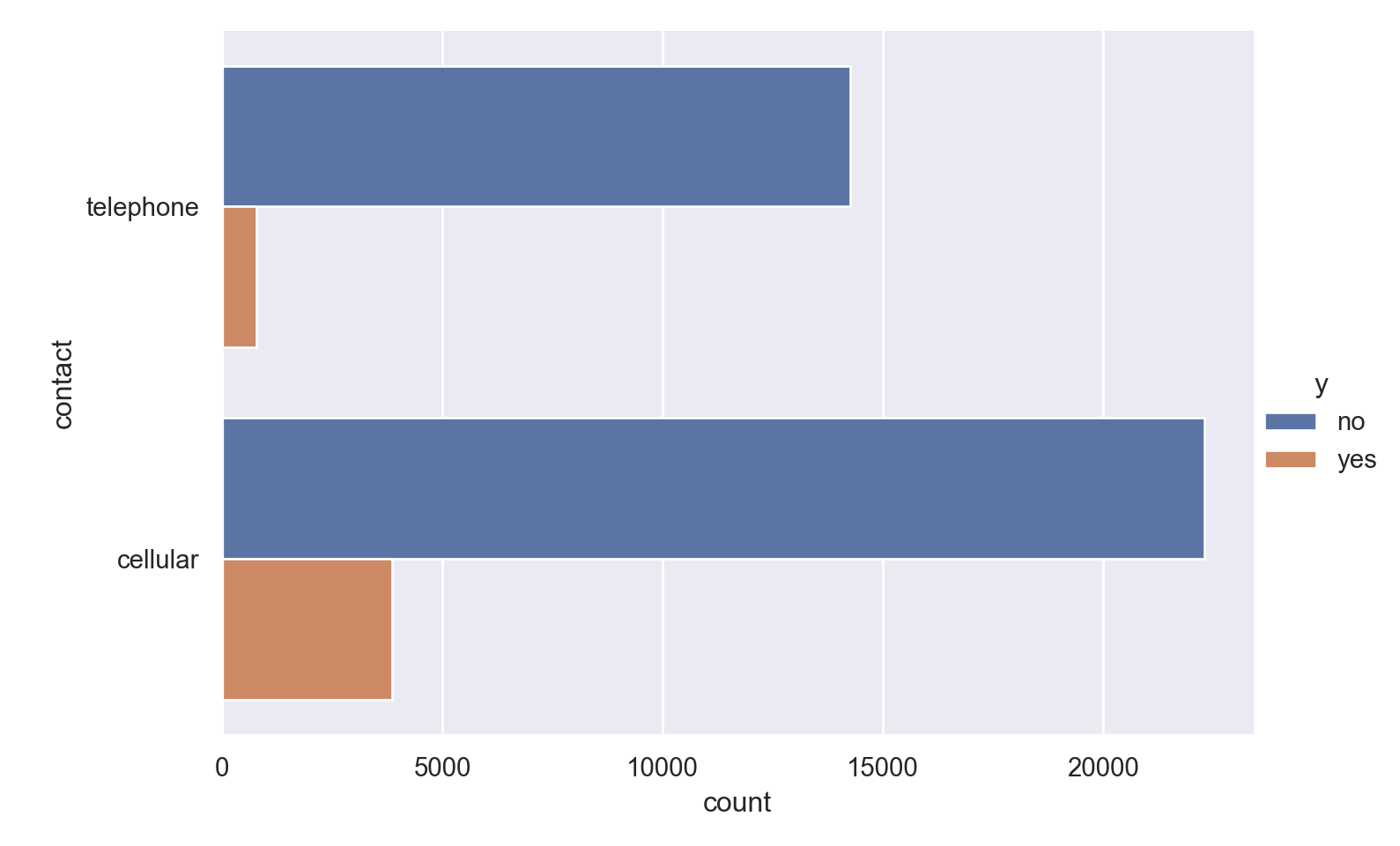
knitr::kable(get_proportions(data_bank_marketing, 'contact', 'y') %>% rename(contact = rowname) %>% rename(overall = n) %>% arrange(desc(yes)))| contact | no | yes | overall |
|---|---|---|---|
| cellular | 85.26239 | 14.737607 | 63.4748 |
| telephone | 94.76868 | 5.231321 | 36.5252 |
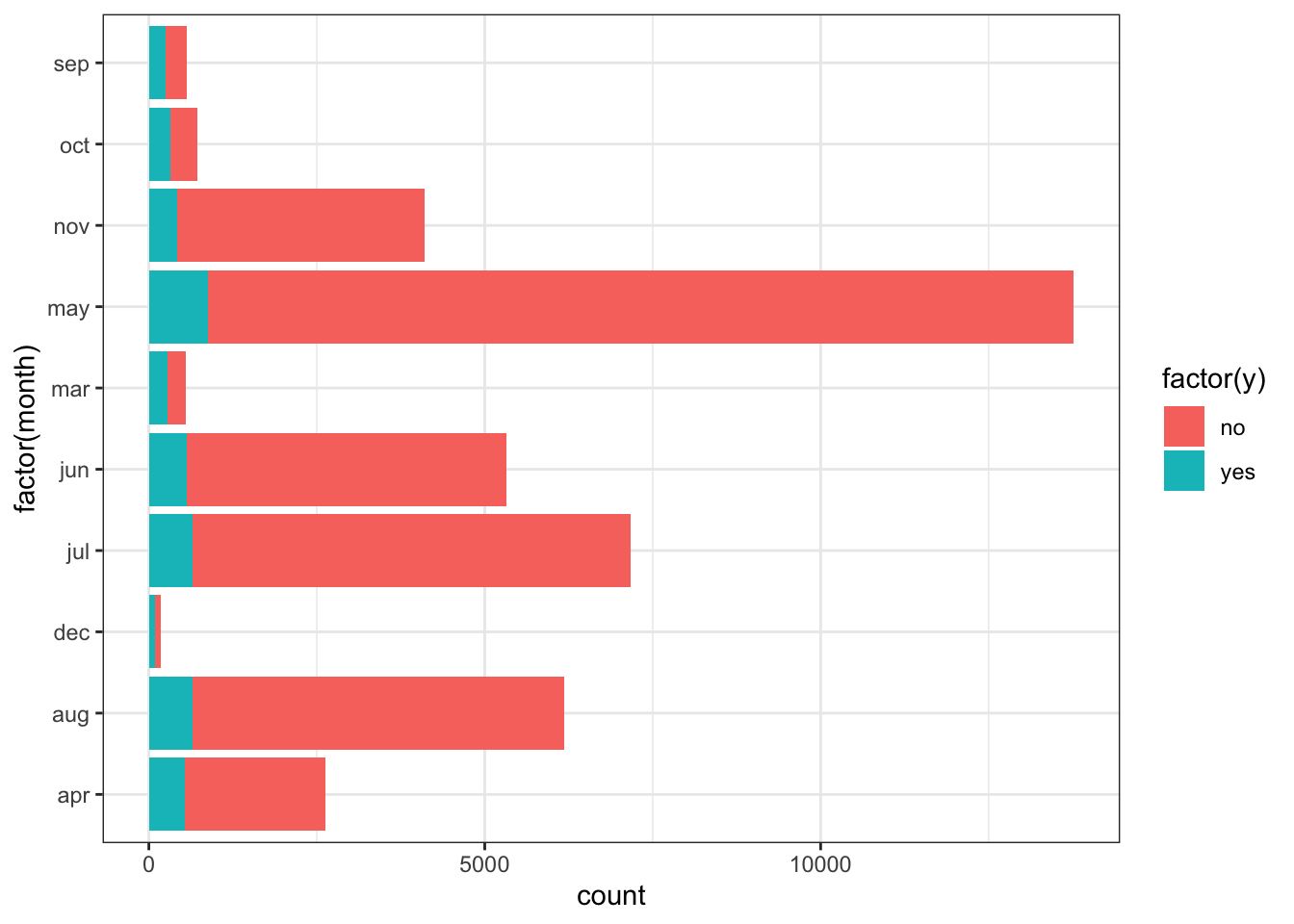
knitr::kable(get_proportions(data_bank_marketing, 'month', 'y') %>% rename(month = rowname) %>% rename(overall = n) %>% arrange(desc(yes)))| month | no | yes | overall |
|---|---|---|---|
| mar | 49.45055 | 50.549450 | 1.3256288 |
| dec | 51.09890 | 48.901099 | 0.4418763 |
| sep | 55.08772 | 44.912281 | 1.3838982 |
| oct | 56.12813 | 43.871866 | 1.7432262 |
| apr | 79.52128 | 20.478723 | 6.3902107 |
| aug | 89.39786 | 10.602137 | 14.9995144 |
| jun | 89.48853 | 10.511470 | 12.9115276 |
| nov | 89.85613 | 10.143867 | 9.9567835 |
| jul | 90.95344 | 9.046557 | 17.4176945 |
| may | 93.56526 | 6.434745 | 33.4296397 |
knitr::kable(get_proportions(data_bank_marketing, 'poutcome', 'y') %>% rename(poutcome = rowname) %>% rename(overall = n) %>% arrange(desc(yes)))| poutcome | no | yes | overall |
|---|---|---|---|
| success | 34.88711 | 65.112892 | 3.333495 |
| failure | 85.77140 | 14.228598 | 10.323395 |
| nonexistent | 91.16779 | 8.832213 | 86.343110 |
knitr::kable(get_proportions(data_bank_marketing, 'day_of_week', 'y') %>% rename(day_of_week = rowname) %>% rename(overall = n) %>% arrange(desc(yes)))| day_of_week | no | yes | overall |
|---|---|---|---|
| thu | 87.88125 | 12.11875 | 20.93571 |
| tue | 88.22002 | 11.77998 | 19.64164 |
| wed | 88.33292 | 11.66708 | 19.74847 |
| fri | 89.19126 | 10.80874 | 19.00311 |
| mon | 90.05168 | 9.94832 | 20.67107 |
def get_proportions(df, category, outcome):
df=data_bank_marketing[[category,outcome]].groupby(category).value_counts(normalize=True).mul(100)
df_overall=data_bank_marketing[[category]].groupby(category)
df_overall=(df_overall.value_counts()/sum(df_overall.value_counts())).mul(100)
df_overall=pd.DataFrame(df_overall).reset_index()
df_overall=df_overall.rename(columns={0:'overall'})
df_yes=df.iloc[1::2]
df_yes=pd.DataFrame(df_yes).reset_index().drop([outcome], axis = 1)
df_yes=df_yes.rename(columns={0:'yes'})
df_no=df.iloc[::2]
df_no=pd.DataFrame(df_no).reset_index().drop([outcome], axis = 1)
df_no=df_no.rename(columns={0:'no'})
final_df = df_no.join(df_yes['yes'])
final_df = final_df.join(df_overall['overall']).sort_values('yes', ascending=False)
return final_df
proportions=get_proportions(data_bank_marketing,'job', 'y')
dsp.Markdown(proportions.to_markdown(index=False))| job | no | yes | overall |
|---|---|---|---|
| student | 68.5714 | 31.4286 | 2.12441 |
| retired | 74.7674 | 25.2326 | 4.17597 |
| unemployed | 85.7988 | 14.2012 | 2.46188 |
| admin. | 87.0274 | 12.9726 | 25.3035 |
| management | 88.7825 | 11.2175 | 7.09916 |
| unknown | 88.7879 | 11.2121 | 0.801204 |
| technician | 89.174 | 10.826 | 16.3713 |
| self-employed | 89.5144 | 10.4856 | 3.45003 |
| housemaid | 90 | 10 | 2.57357 |
| entrepreneur | 91.4835 | 8.51648 | 3.53501 |
| services | 91.8619 | 8.13807 | 9.6363 |
| blue-collar | 93.1057 | 6.89432 | 22.4677 |
proportions=get_proportions(data_bank_marketing,'education', 'y')
dsp.Markdown(proportions.to_markdown(index=False))| education | no | yes | overall |
|---|---|---|---|
| illiterate | 77.7778 | 22.2222 | 0.043702 |
| unknown | 85.4997 | 14.5003 | 4.20268 |
| university.degree | 86.2755 | 13.7245 | 29.5426 |
| professional.course | 88.6515 | 11.3485 | 12.7294 |
| high.school | 89.1645 | 10.8355 | 23.1014 |
| basic.4y | 89.751 | 10.249 | 10.1389 |
| basic.6y | 91.7976 | 8.20244 | 5.56473 |
| basic.9y | 92.1754 | 7.82465 | 14.6766 |
proportions=get_proportions(data_bank_marketing, 'marital', 'y')
dsp.Markdown(proportions.to_markdown(index=False))| marital | no | yes | overall |
|---|---|---|---|
| unknown | 85 | 15 | 0.194231 |
| single | 85.9959 | 14.0041 | 28.0859 |
| divorced | 89.6791 | 10.3209 | 11.1974 |
| married | 89.8427 | 10.1573 | 60.5225 |
proportions=get_proportions(data_bank_marketing, 'default', 'y')
dsp.Markdown(proportions.to_markdown(index=False))| default | no | yes | overall |
|---|---|---|---|
| no | 87.121 | 12.879 | 79.1201 |
| unknown | 94.847 | 5.15296 | 20.8726 |
| yes | 100 | nan | 0.00728367 |
proportions=get_proportions(data_bank_marketing, 'housing', 'y')
dsp.Markdown(proportions.to_markdown(index=False))| housing | no | yes | overall |
|---|---|---|---|
| yes | 88.3806 | 11.6194 | 52.3842 |
| no | 89.1204 | 10.8796 | 45.2122 |
| unknown | 89.1919 | 10.8081 | 2.40361 |
proportions=get_proportions(data_bank_marketing, 'loan', 'y')
dsp.Markdown(proportions.to_markdown(index=False))| loan | no | yes | overall |
|---|---|---|---|
| no | 88.6598 | 11.3402 | 82.4269 |
| yes | 89.0685 | 10.9315 | 15.1695 |
| unknown | 89.1919 | 10.8081 | 2.40361 |
proportions=get_proportions(data_bank_marketing, 'contact', 'y')
dsp.Markdown(proportions.to_markdown(index=False))| contact | no | yes | overall |
|---|---|---|---|
| cellular | 85.2624 | 14.7376 | 63.4748 |
| telephone | 94.7687 | 5.23132 | 36.5252 |
proportions=get_proportions(data_bank_marketing, 'month', 'y')
dsp.Markdown(proportions.to_markdown(index=False))| month | no | yes | overall |
|---|---|---|---|
| mar | 50.5495 | 49.4505 | 1.32563 |
| dec | 51.0989 | 48.9011 | 0.441876 |
| sep | 55.0877 | 44.9123 | 1.3839 |
| oct | 56.1281 | 43.8719 | 1.74323 |
| apr | 79.5213 | 20.4787 | 6.39021 |
| aug | 89.3979 | 10.6021 | 14.9995 |
| jun | 89.4885 | 10.5115 | 12.9115 |
| nov | 89.8561 | 10.1439 | 9.95678 |
| jul | 90.9534 | 9.04656 | 17.4177 |
| may | 93.5653 | 6.43474 | 33.4296 |
proportions=get_proportions(data_bank_marketing, 'poutcome', 'y')
dsp.Markdown(proportions.to_markdown(index=False))| poutcome | no | yes | overall |
|---|---|---|---|
| success | 65.1129 | 34.8871 | 3.3335 |
| failure | 85.7714 | 14.2286 | 10.3234 |
| nonexistent | 91.1678 | 8.83221 | 86.3431 |
proportions=get_proportions(data_bank_marketing, 'day_of_week', 'y')
dsp.Markdown(proportions.to_markdown(index=False))| day_of_week | no | yes | overall |
|---|---|---|---|
| thu | 87.8812 | 12.1188 | 20.9357 |
| tue | 88.22 | 11.78 | 19.6416 |
| wed | 88.3329 | 11.6671 | 19.7485 |
| fri | 89.1913 | 10.8087 | 19.0031 |
| mon | 90.0517 | 9.94832 | 20.6711 |
function get_proportions(df::DataFrame, category::String, outcome::String, filter_str::String)
gdf_outcome = groupby(df, [category, outcome])
D = DataFrame(combine(gdf_outcome, nrow))
counts_1=@chain D begin
filter(outcome => isequal(filter_str), _)
select(:nrow)
end
counts_2=@chain D begin
filter(outcome => !isequal(filter_str), _)
select(:nrow)
end
if nrow(counts_1) != nrow(counts_2)
diff = nrow(counts_1) - nrow(counts_2)
U = counts_1
if diff > 0 #counts_1 has more rows
U = counts_2
end
i=0
while i < abs(diff)
push!(U, [0])
i += 1
end
end
rename!(counts_1, :nrow=>:yes)
rename!(counts_2, :nrow=>:no)
counts=DataFrame(hcat(counts_1,counts_2))
@transform!(counts, :all = :yes .+ :no)
@transform!(counts, :prop = :yes ./ :all)
@transform!(counts, :overall = :all ./ nrow(df))
counts.prop .*= 100
counts.overall .*= 100
N = unique(select(D, category))
sort!(hcat(N,select(counts,[:prop,:overall])), :prop, rev=true)
endget_proportions (generic function with 1 method)12×3 DataFrame
Row │ job prop overall
│ String15 Float64 Float64
─────┼────────────────────────────────────
1 │ student 31.4286 2.12441
2 │ retired 25.2326 4.17597
3 │ unemployed 14.2012 2.46188
4 │ admin. 12.9726 25.3035
5 │ management 11.2175 7.09916
6 │ unknown 11.2121 0.801204
7 │ technician 10.826 16.3713
8 │ self-employed 10.4856 3.45003
9 │ housemaid 10.0 2.57357
10 │ entrepreneur 8.51648 3.53501
11 │ services 8.13807 9.6363
12 │ blue-collar 6.89432 22.46778×3 DataFrame
Row │ education prop overall
│ String31 Float64 Float64
─────┼──────────────────────────────────────────
1 │ illiterate 22.2222 0.043702
2 │ unknown 14.5003 4.20268
3 │ university.degree 13.7245 29.5426
4 │ professional.course 11.3485 12.7294
5 │ high.school 10.8355 23.1014
6 │ basic.4y 10.249 10.1389
7 │ basic.6y 8.20244 5.56473
8 │ basic.9y 7.82465 14.67664×3 DataFrame
Row │ marital prop overall
│ String15 Float64 Float64
─────┼──────────────────────────────
1 │ unknown 15.0 0.194231
2 │ single 14.0041 28.0859
3 │ divorced 10.3209 11.1974
4 │ married 10.1573 60.52253×3 DataFrame
Row │ default prop overall
│ String7 Float64 Float64
─────┼────────────────────────────────
1 │ no 12.879 79.1201
2 │ unknown 5.15296 20.8726
3 │ yes 0.0 0.007283673×3 DataFrame
Row │ housing prop overall
│ String7 Float64 Float64
─────┼────────────────────────────
1 │ yes 11.6194 52.3842
2 │ no 10.8796 45.2122
3 │ unknown 10.8081 2.403613×3 DataFrame
Row │ loan prop overall
│ String7 Float64 Float64
─────┼────────────────────────────
1 │ no 11.3402 82.4269
2 │ yes 10.9315 15.1695
3 │ unknown 10.8081 2.403612×3 DataFrame
Row │ contact prop overall
│ String15 Float64 Float64
─────┼──────────────────────────────
1 │ cellular 14.7376 63.4748
2 │ telephone 5.23132 36.525210×3 DataFrame
Row │ month prop overall
│ String3 Float64 Float64
─────┼──────────────────────────────
1 │ mar 50.5495 1.32563
2 │ dec 48.9011 0.441876
3 │ sep 44.9123 1.3839
4 │ oct 43.8719 1.74323
5 │ apr 20.4787 6.39021
6 │ aug 10.6021 14.9995
7 │ jun 10.5115 12.9115
8 │ nov 10.1439 9.95678
9 │ jul 9.04656 17.4177
10 │ may 6.43474 33.4296Observations
job: There is higher percentage of yes outcome for students and retired persons, but the overall proportion of these categories is low. Perhaps a targeted campaign could be fruitful. Among the higher frequencies, admin has higher proportion of yes outcome.
education: There is higher percentage of yes outcome for illiterate - but this number can be ignored as the frequency of the category is negligible. Among the higher frequencies, university.degree has the highest positive outcome.
marital: unknown and single people have the highest positive outcome.
default: Very few people have credit defaults; none of those that do opt for the deposit
housing: Those having housing loans are slightly more likely to opt for the deposit; but the difference is only 1%
contact: Curiously, those contacted on cellular phones have a significantly higher possibility of subscribing to the deposit; this may be worth investigating further to determine causation.
month: For some reason, the months where there were much fewer calls have a much larger chance of subscribing for the loan. This definitely seems to be worthy of further investigation
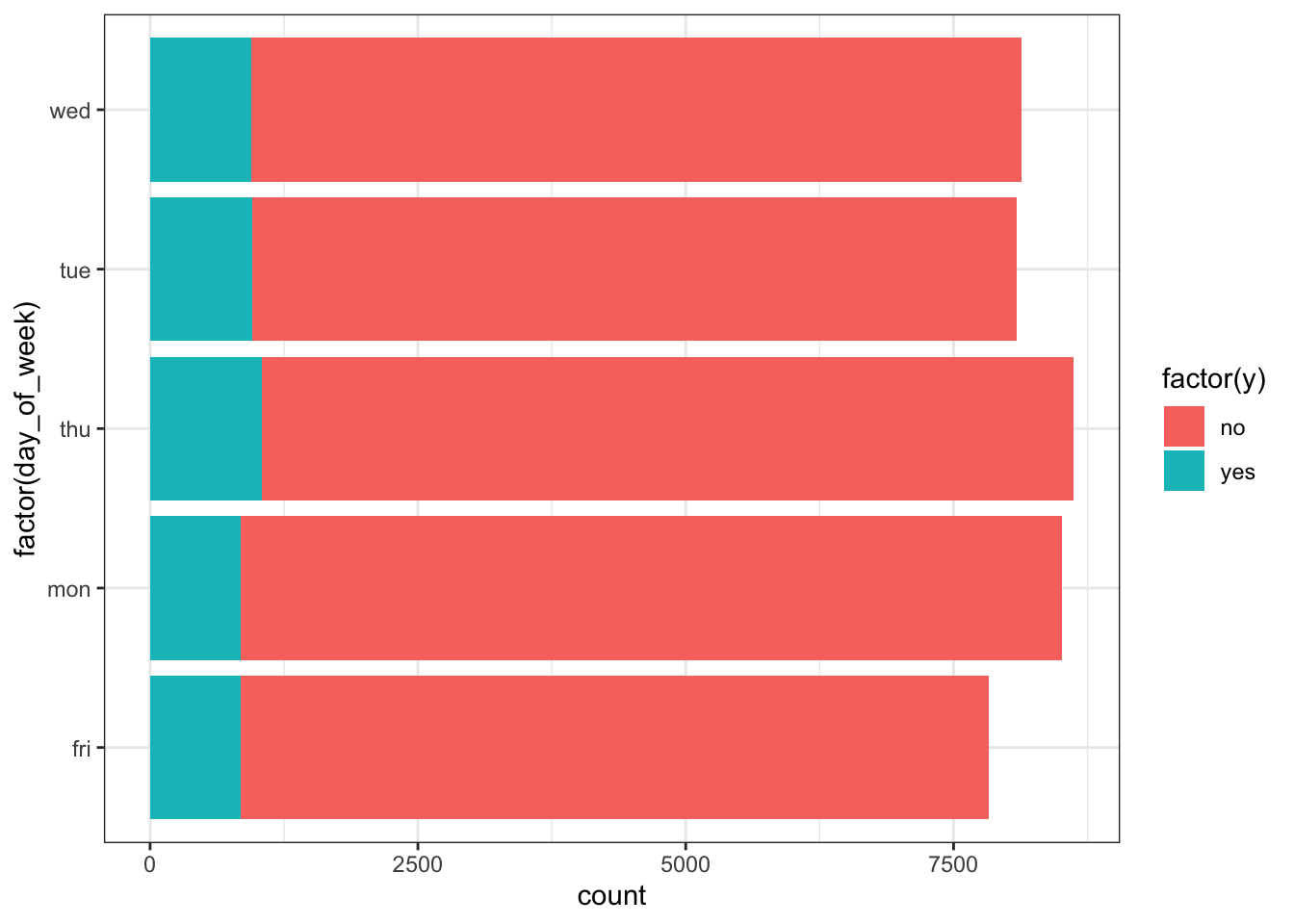
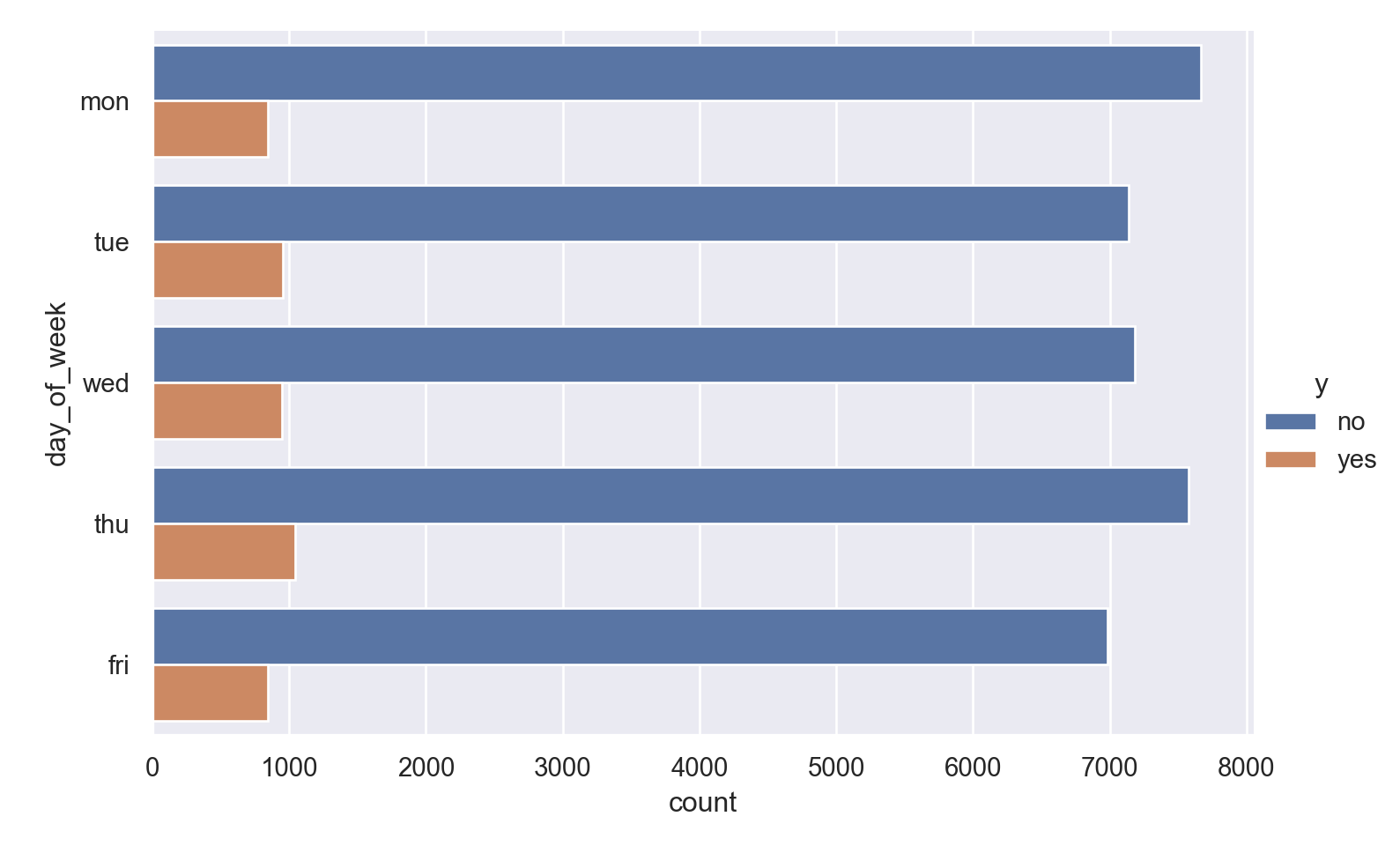
day_of_week: Not a significant difference in outcome across the days of the week; though Thursdays have a slightly higher chance of positive outcome, and Mondays slightly lower.
- Apply relevant transformations to reduce positive and negative skews in the data.
Numeric Attributes
Observations
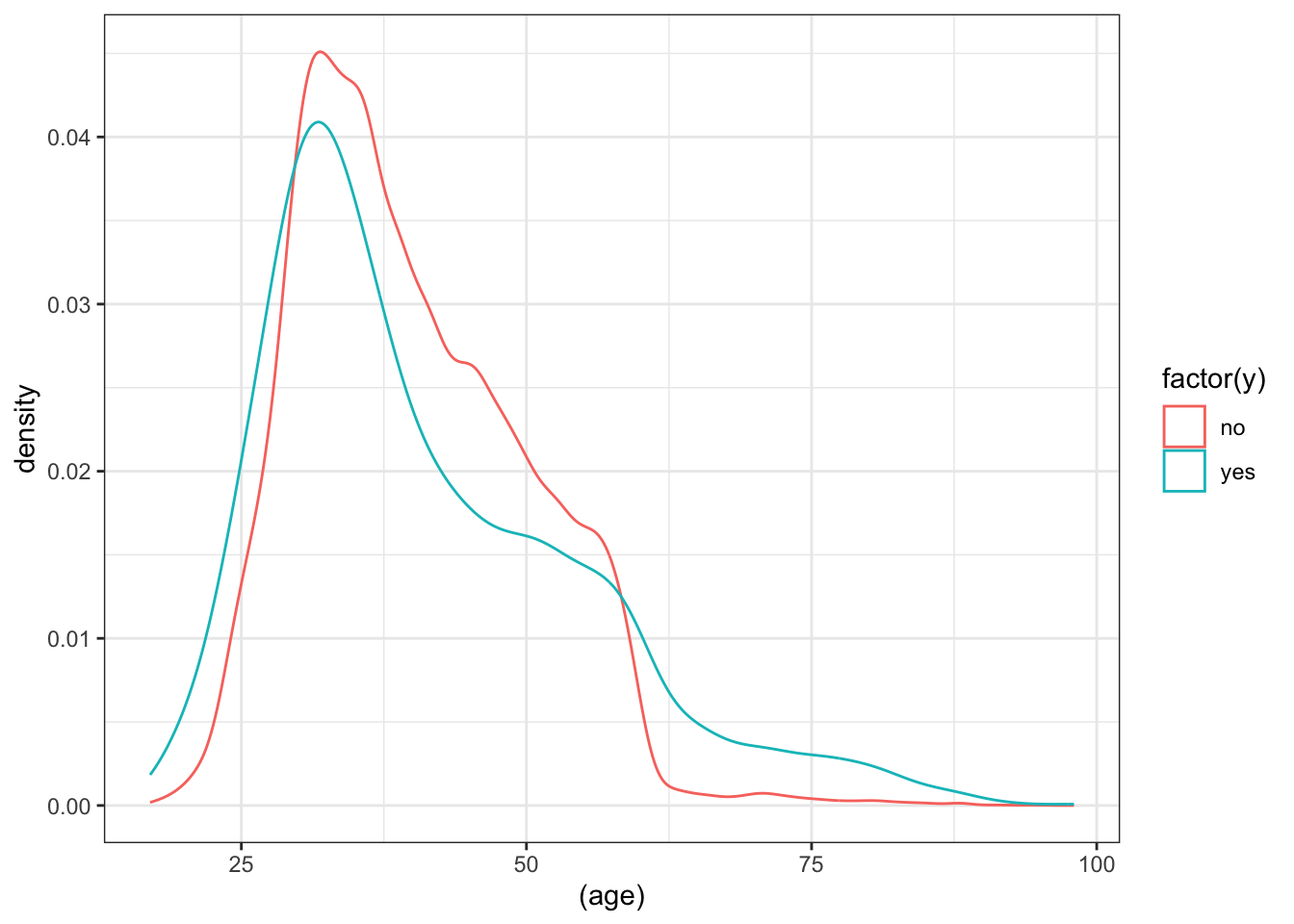
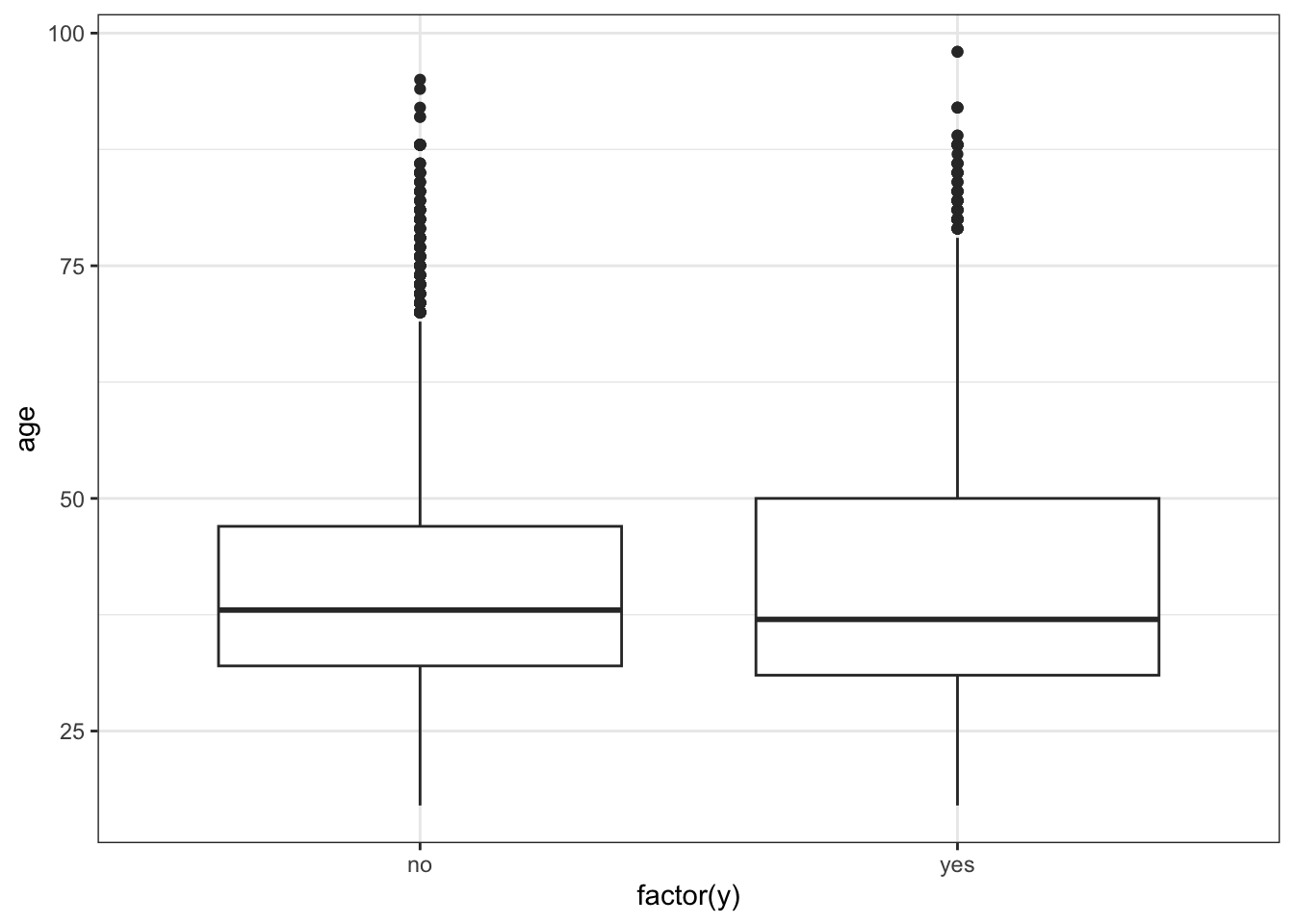
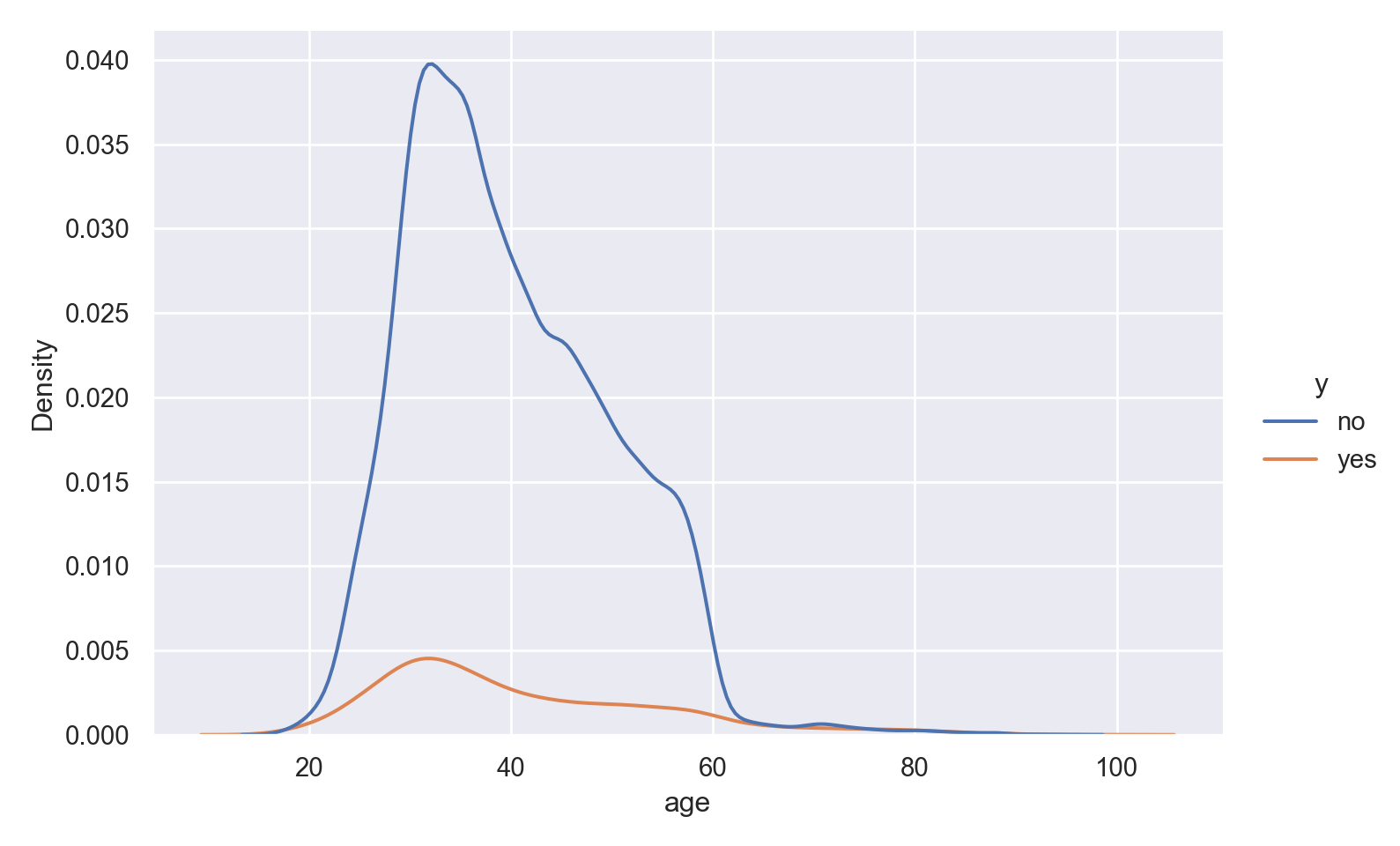
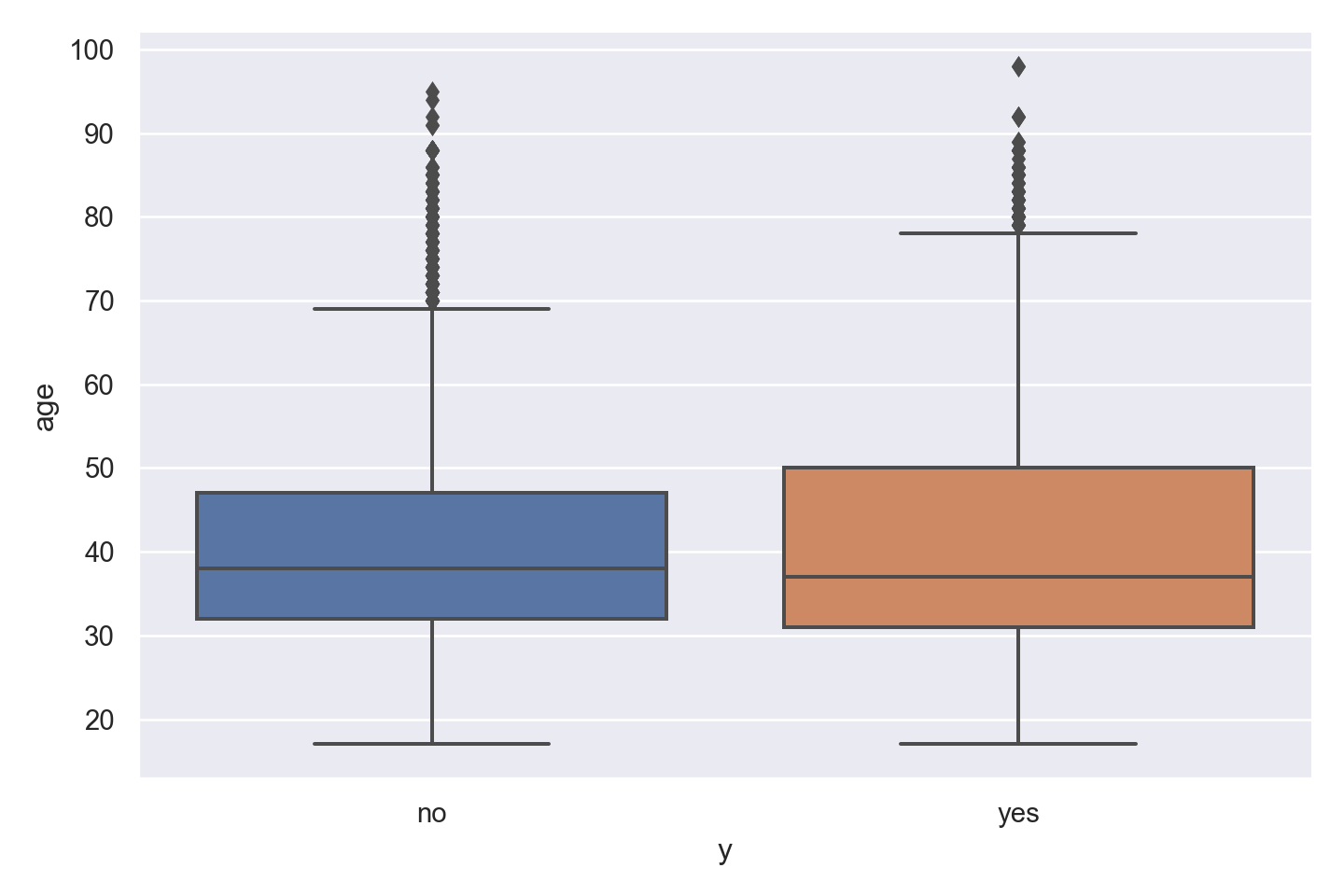
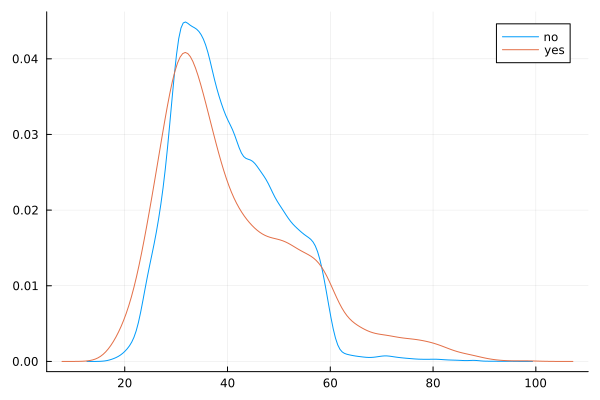
The data is right (positively) skewed, with more younger respondents.
The density curve indicates higher ‘yes’ outcome for age < 26 and age > 60, which was also seen in the numerical inspection.
The boxplot shows slightly more variation for ‘yes’ outcome, but median value of age is similar for both outcomes, with just a slightly lower age associated with ‘yes’ outcome.
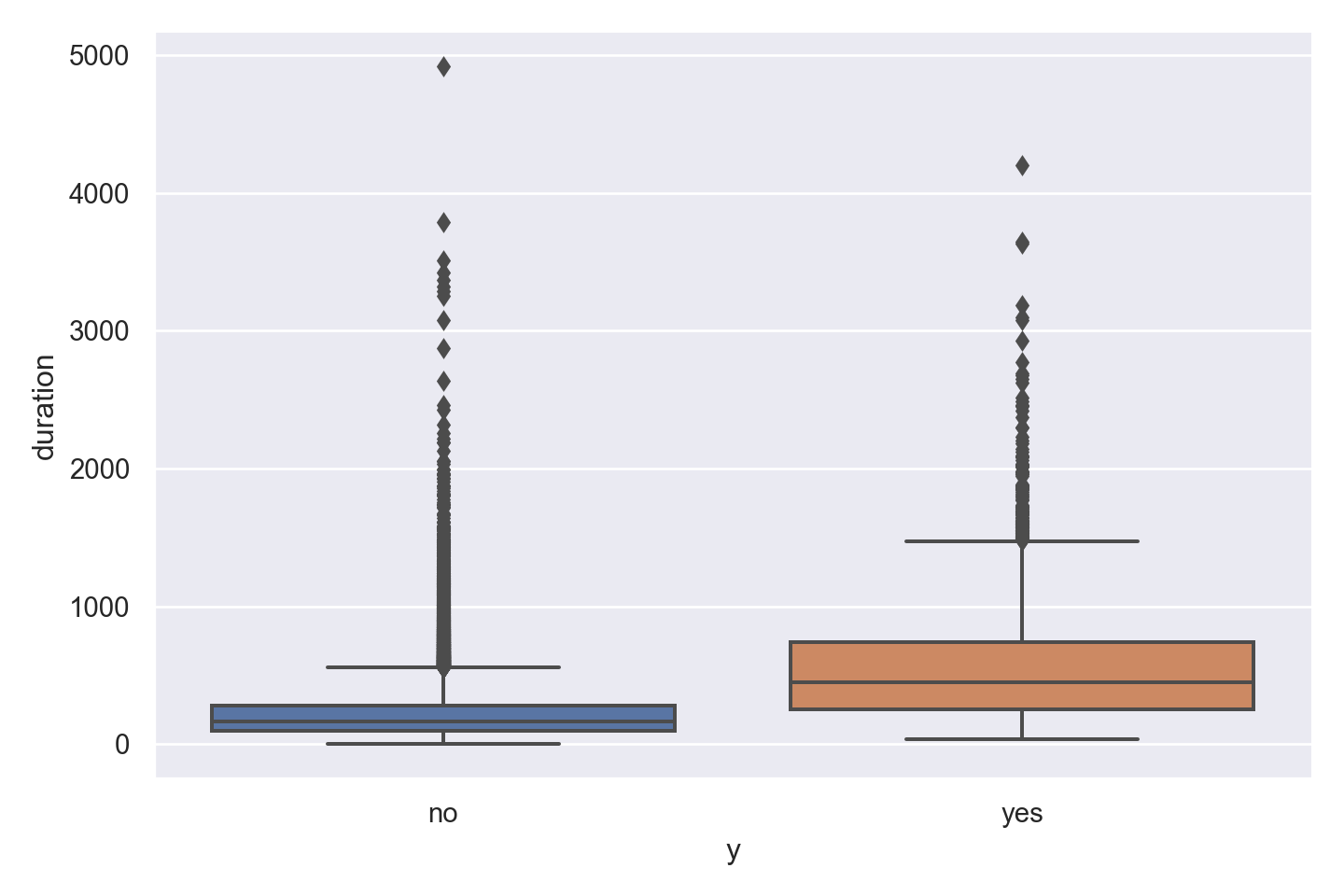
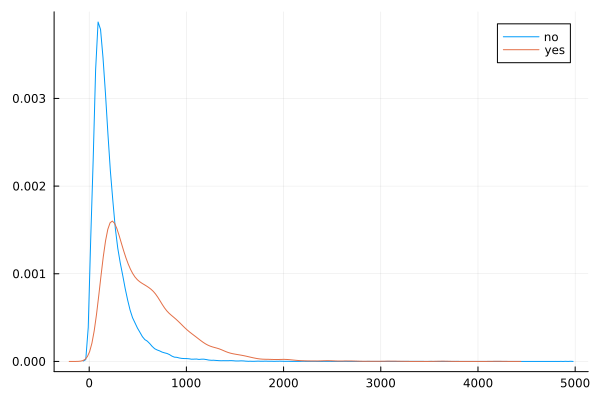
Observations
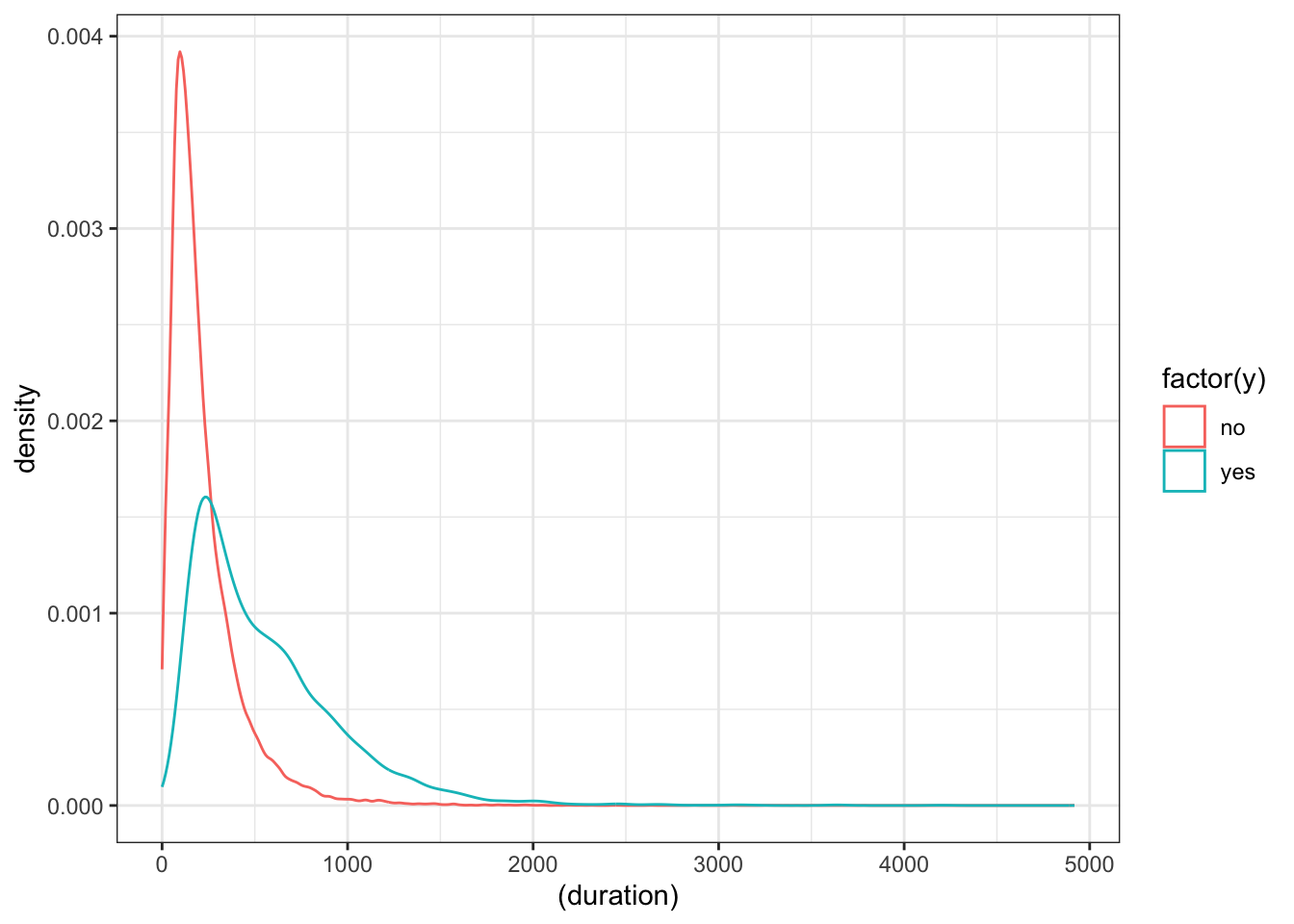
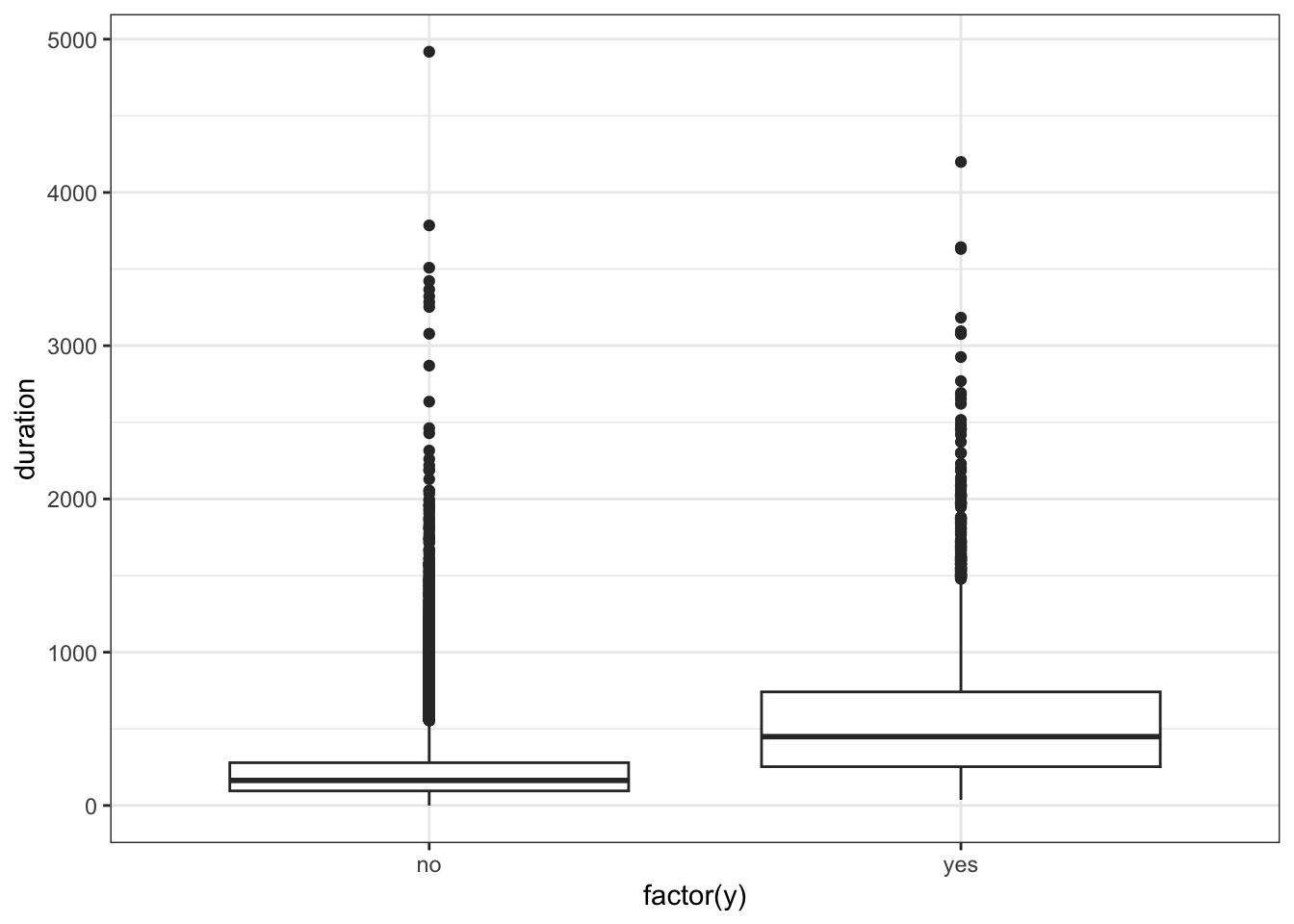
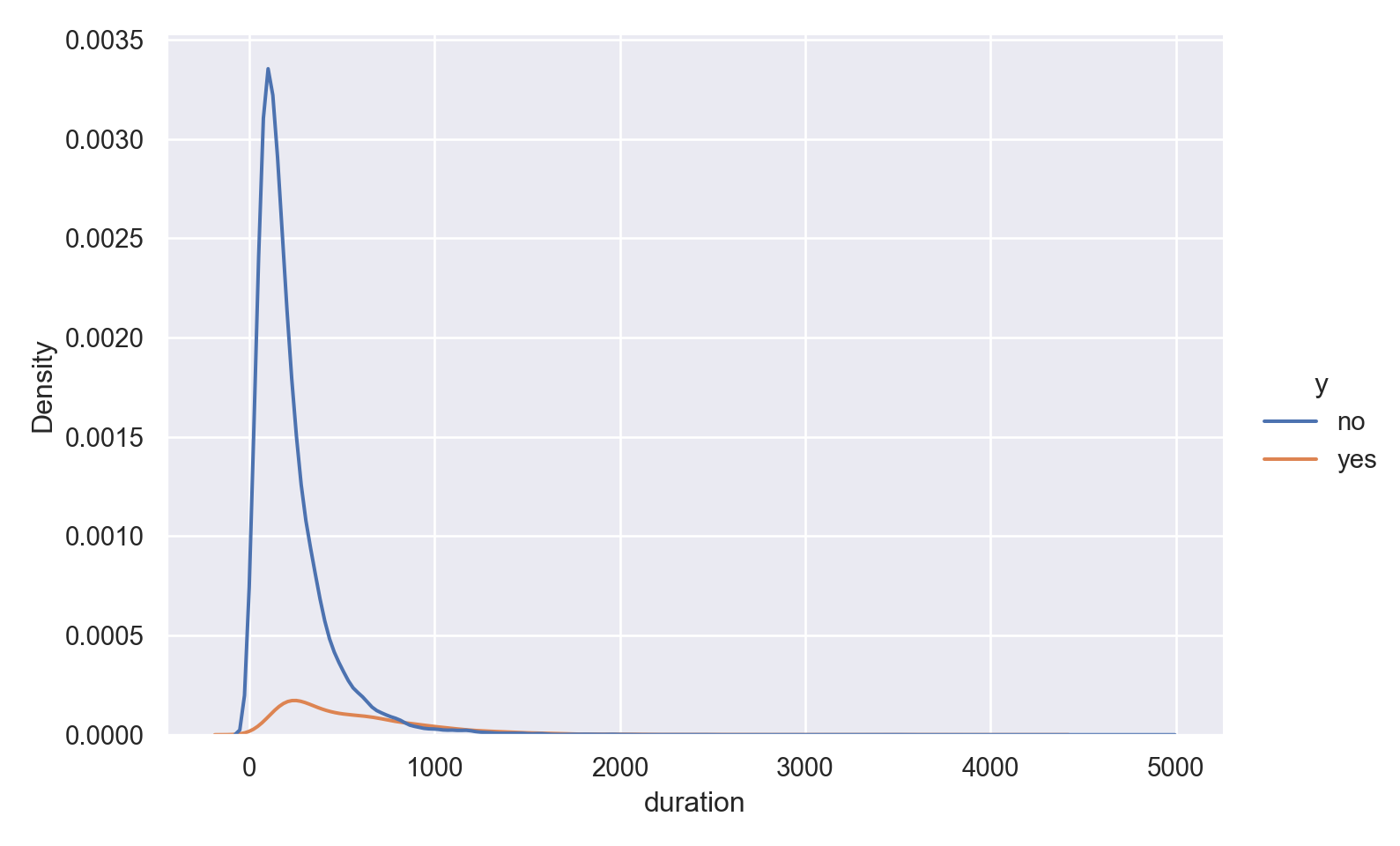
The data is heavily right (positively) skewed, towards low call duration.
As expected, the box plot indicates higher ‘yes’ outcome for higher duration, however as mentioned in the data dictionary, this will not help in predictive modelling as duration is not known before placing a call. It is the result of a ‘yes’ decision, and not its cause.
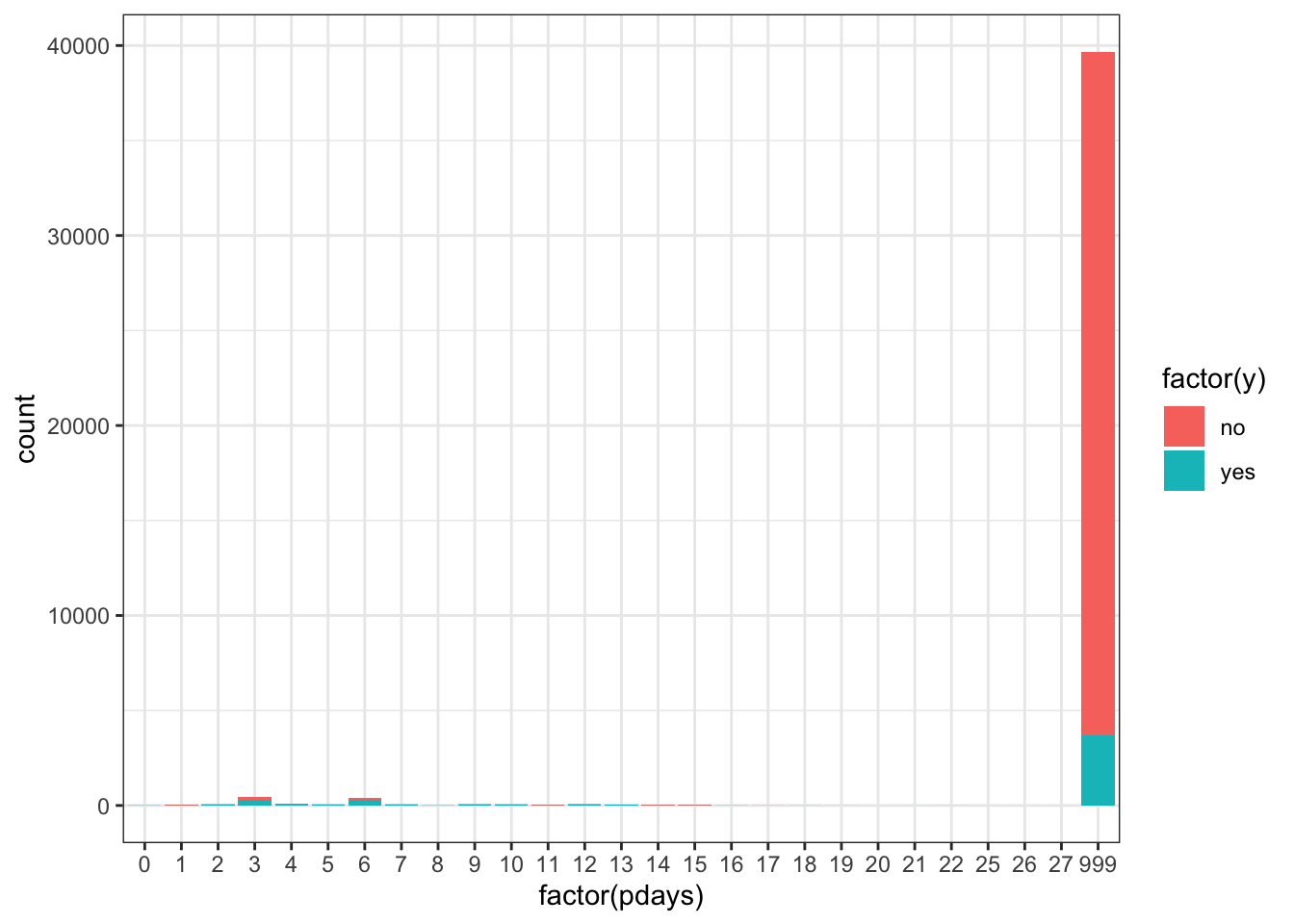
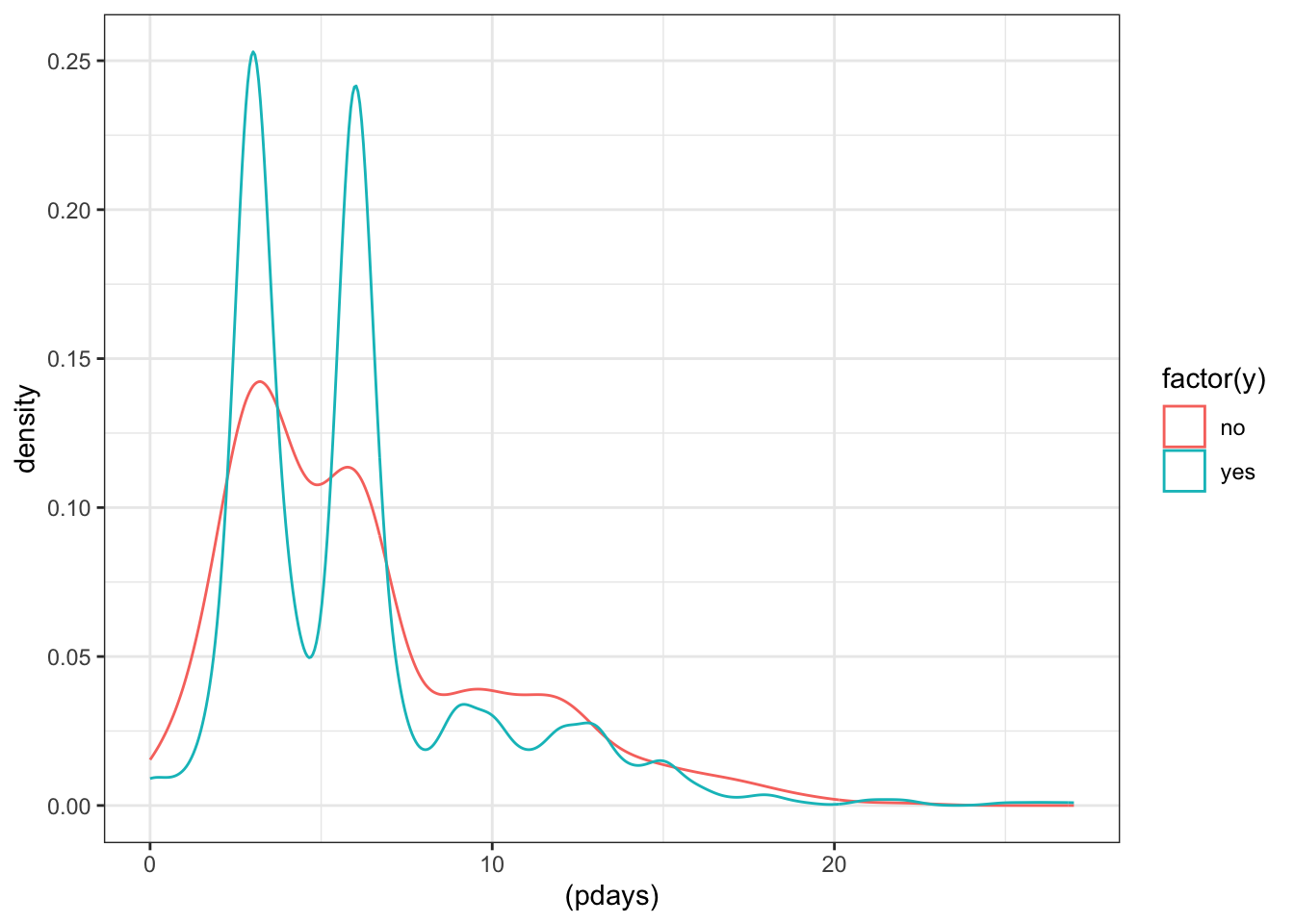
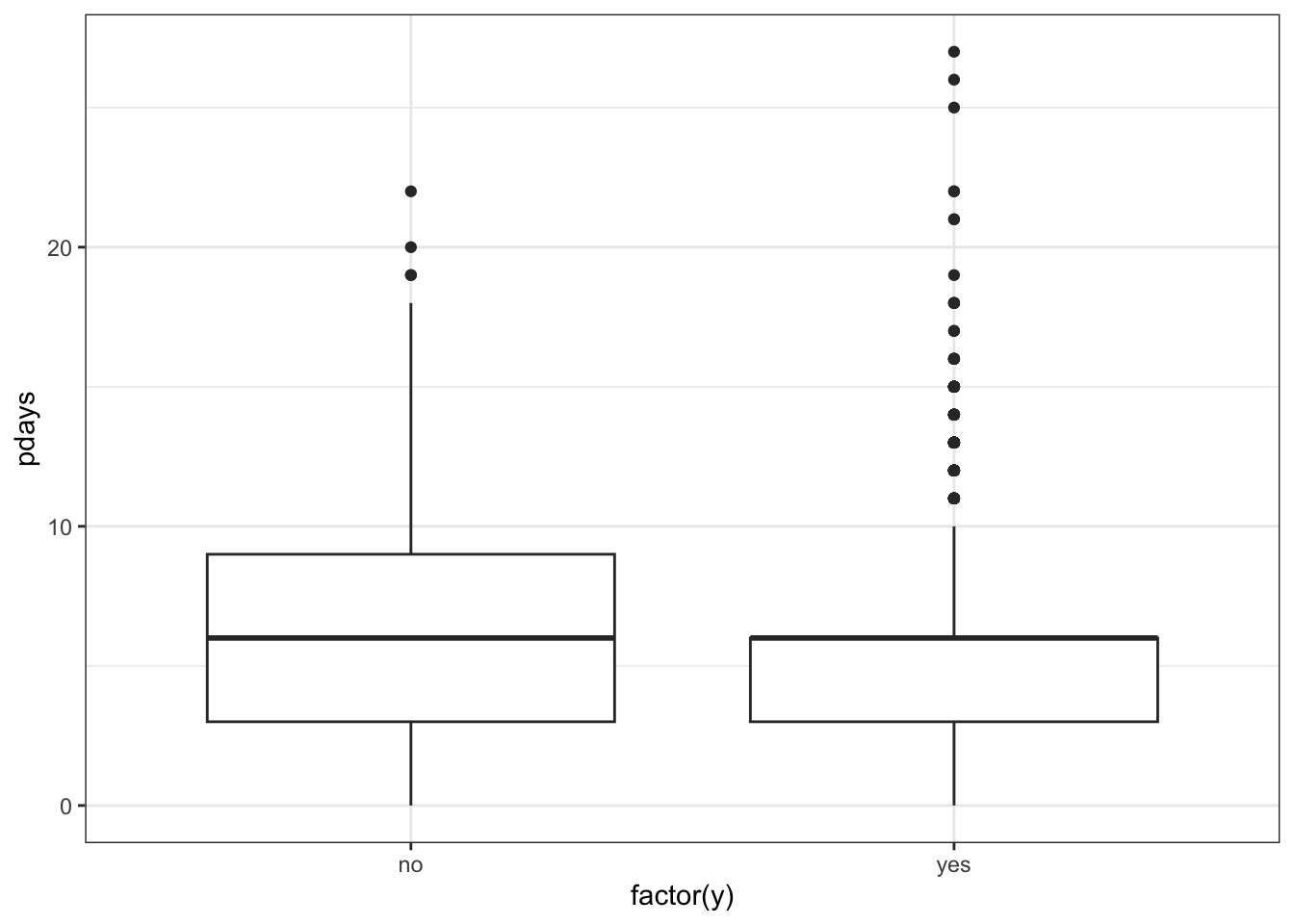
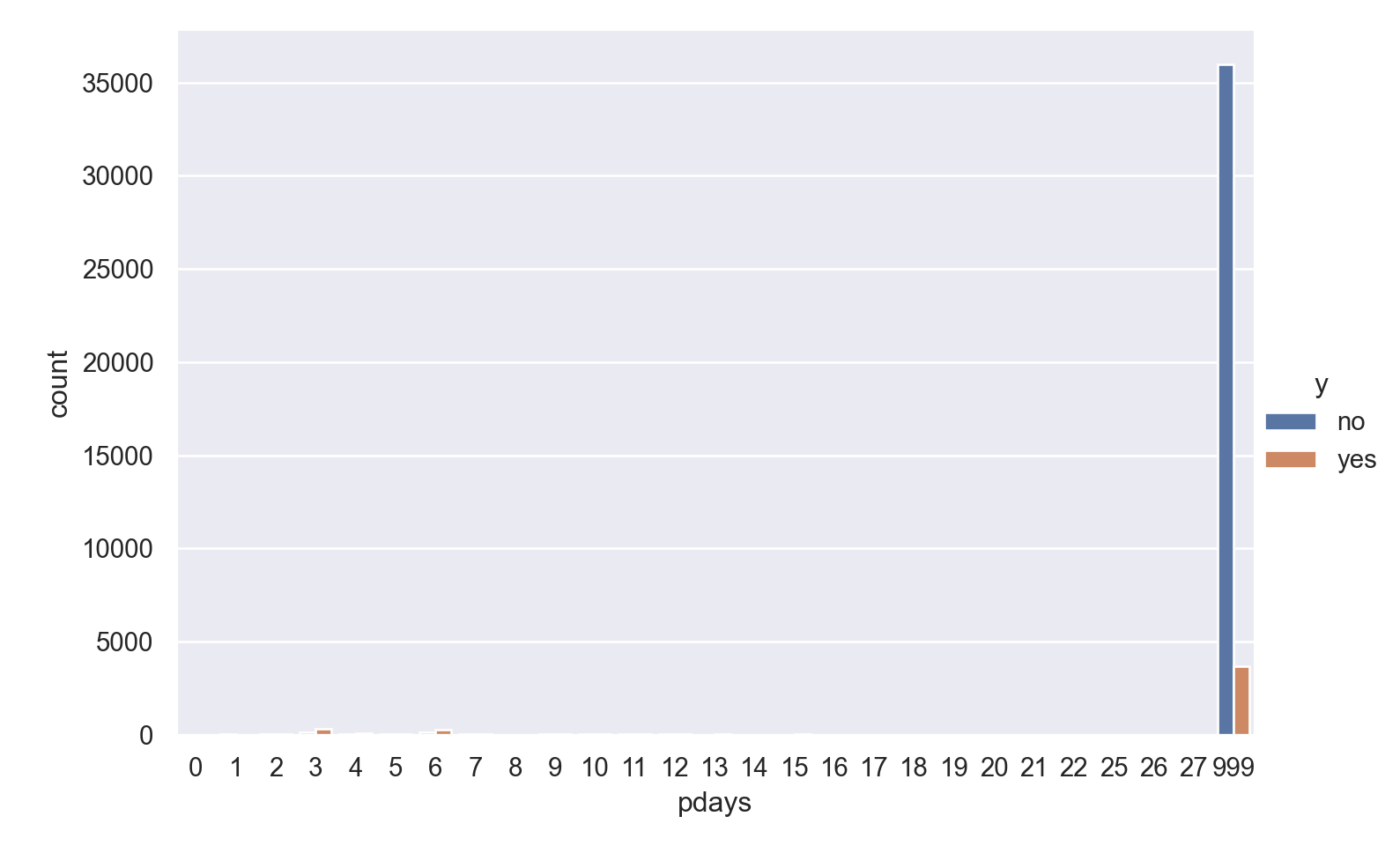
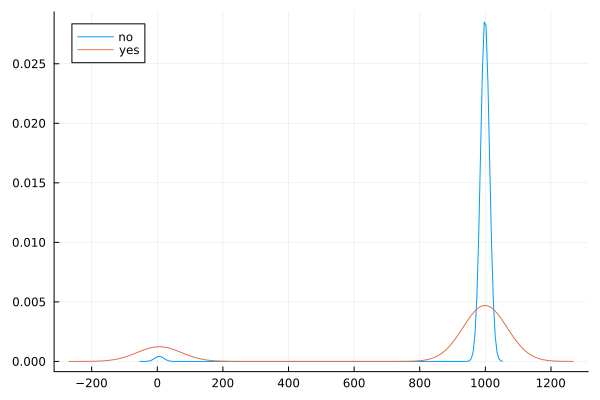
Observations
The vast majority of people were not previously contacted, so there is a very high left skew.
Filtering to only include the previously contacted people reveals a bi-modal pattern in the data, especially for respondents with ‘yes’ outcome.
For those that were previously contacted, median value of days since previous contact is the same for both outcomes, but ‘yes’ outcome has many outliers on the higher end.
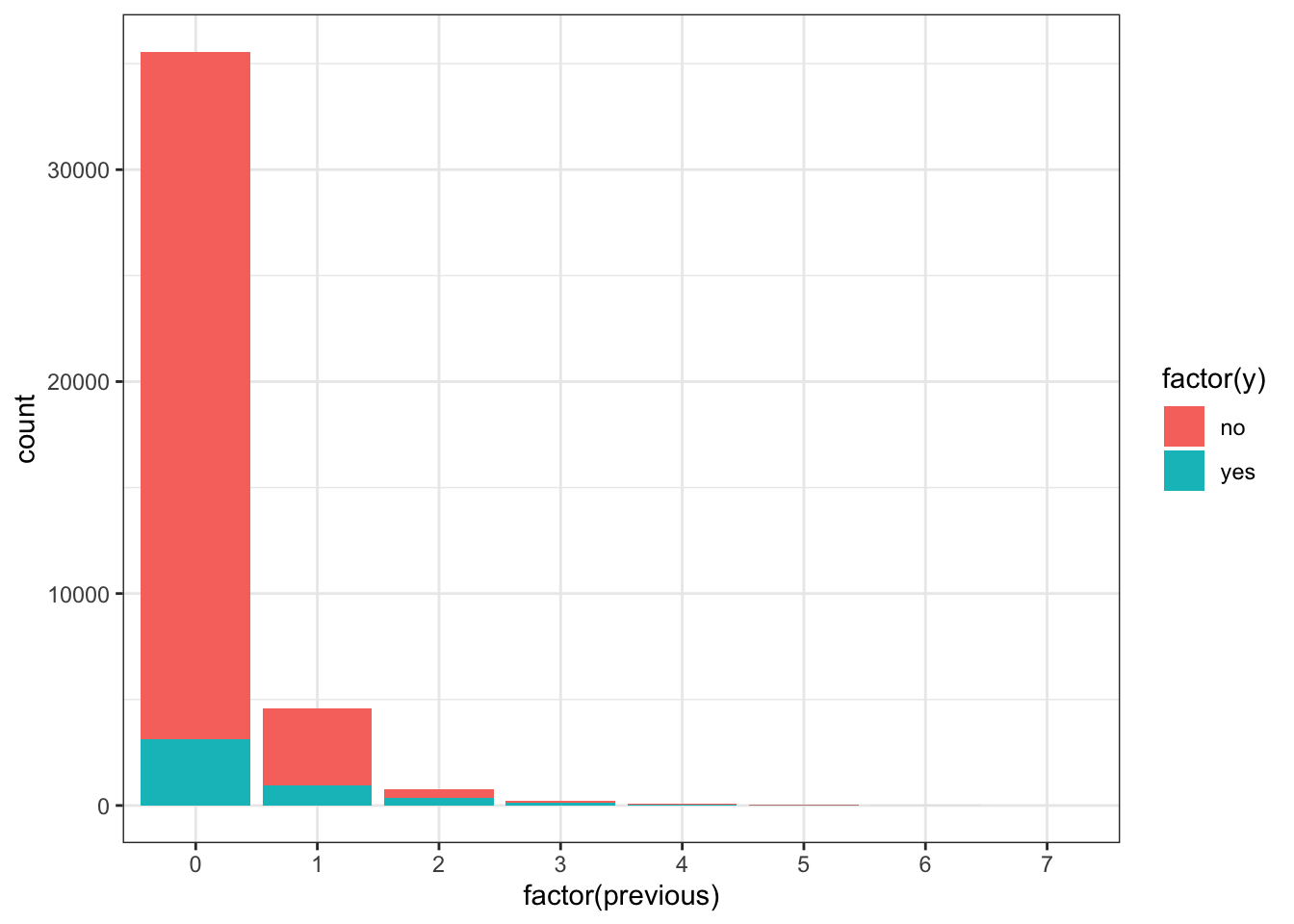
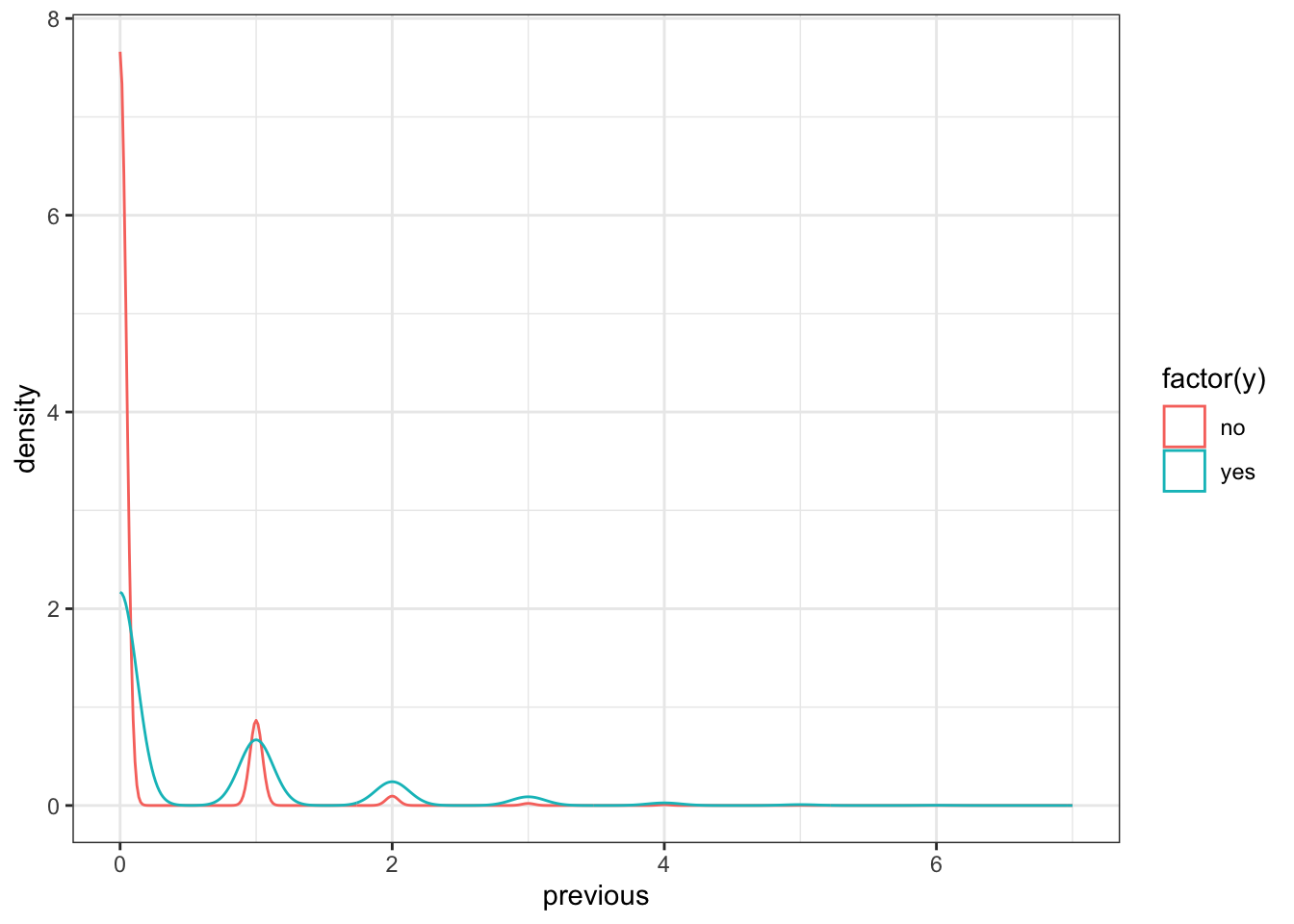
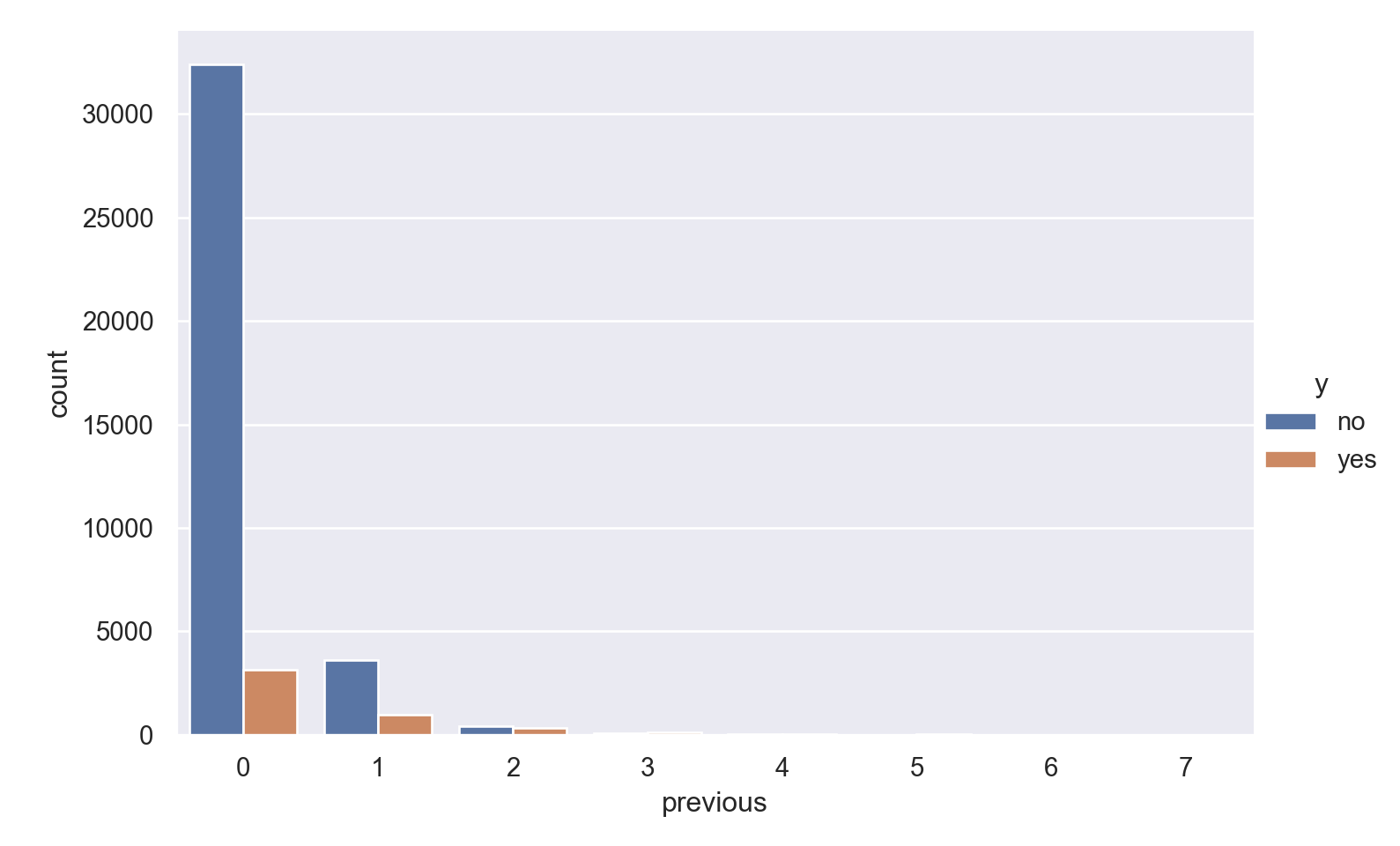
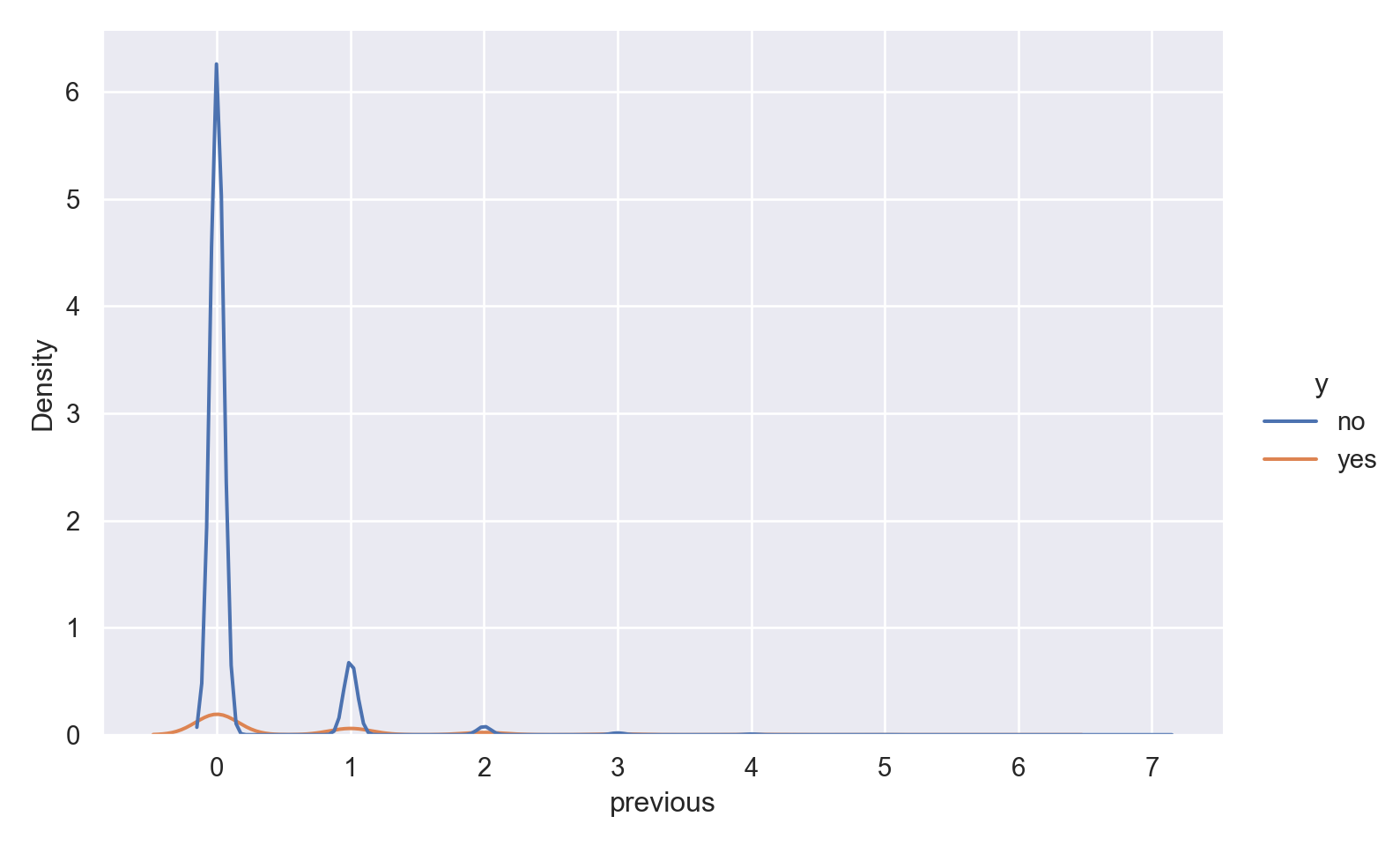
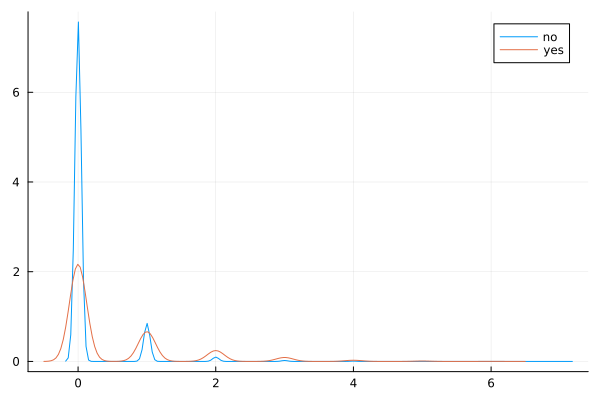
Observations
The vast majority of people were not previously contacted in the previous campaign, so there is a very high right skew.
The few people who were contacted multiple times seem to show higher ‘yes’ outcome for the current campaign.
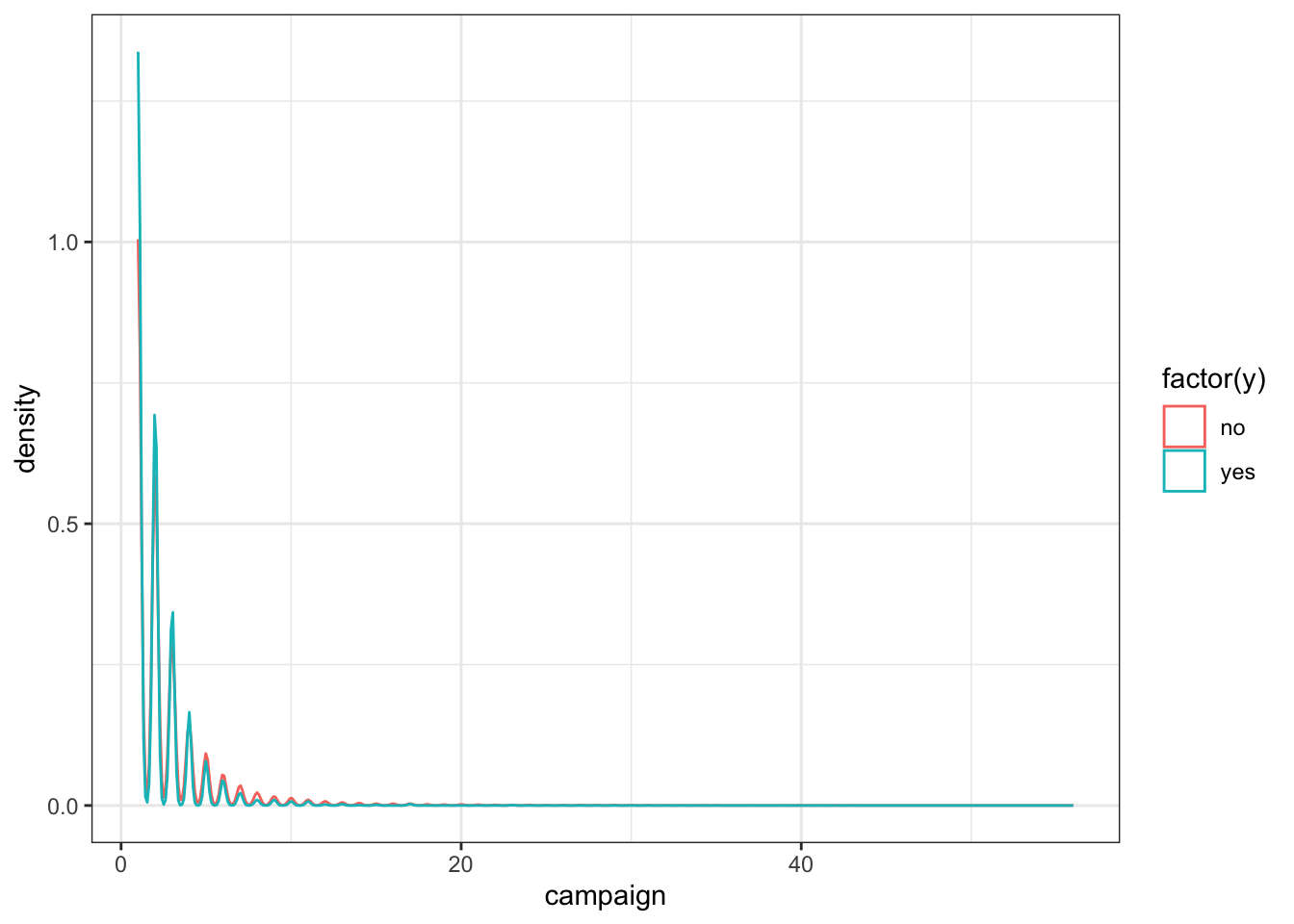
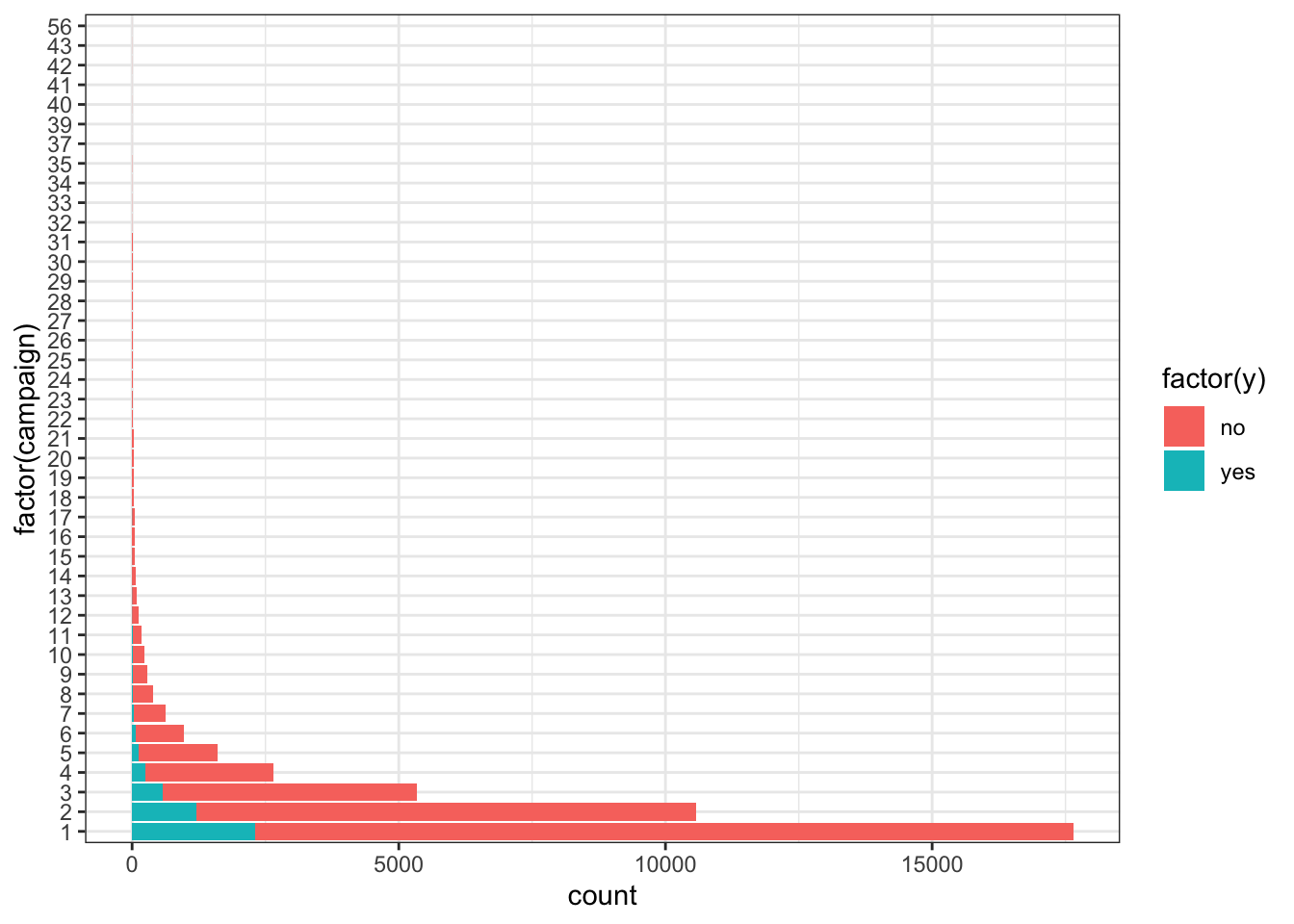
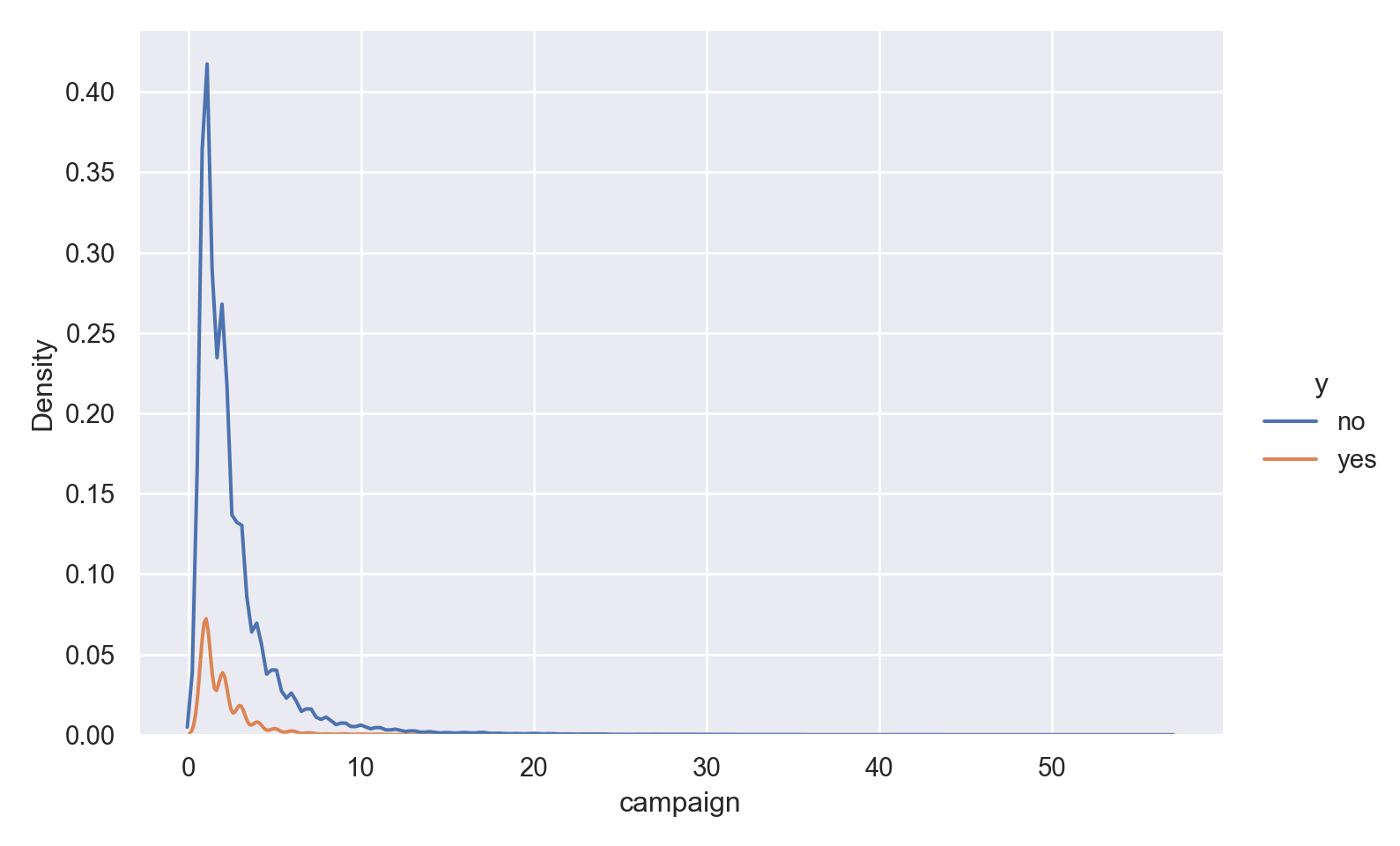
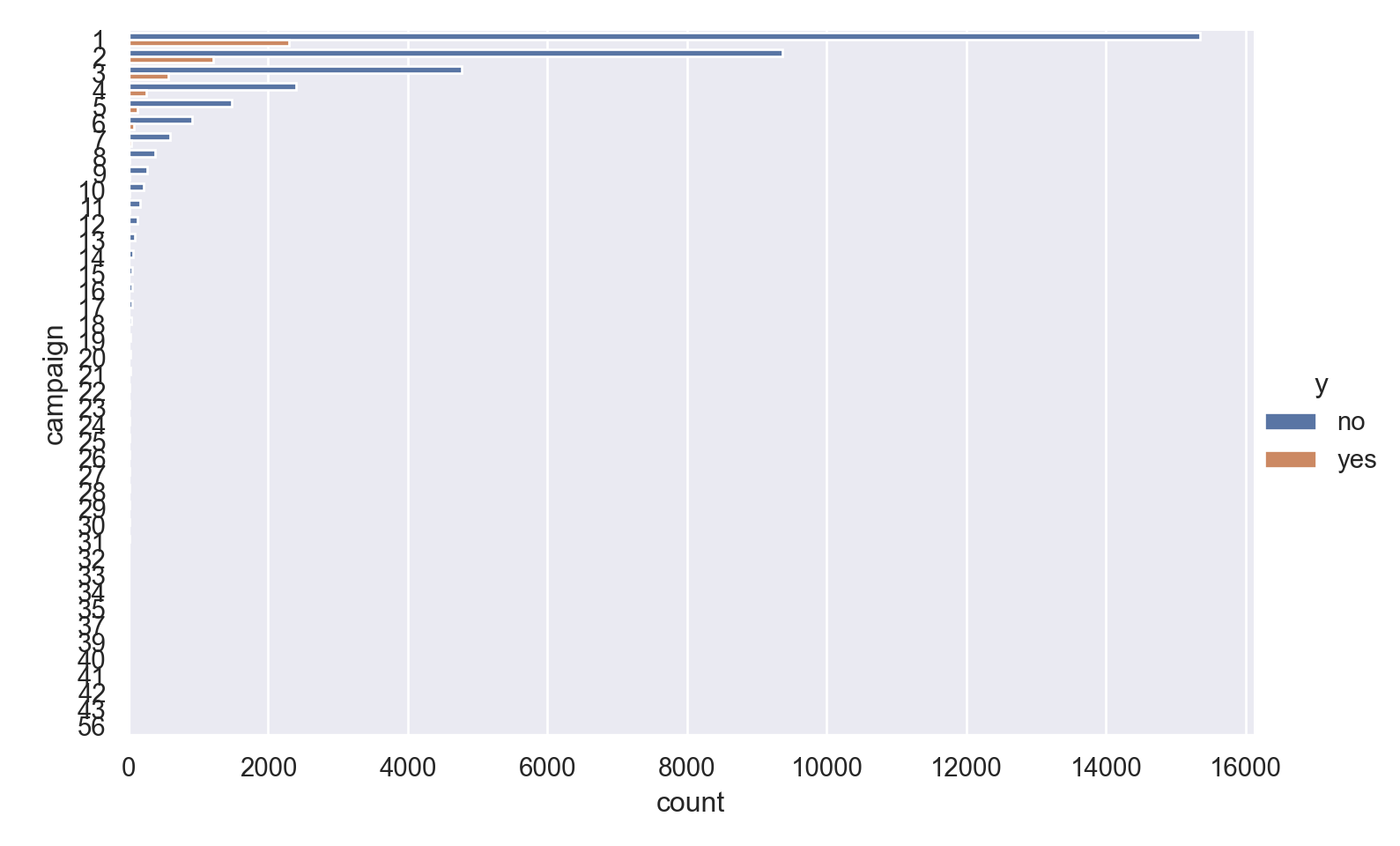
Observations
The vast majority of people were contacted only once in the current campaign, so there is a very high right skew.
The few people who were contacted multiple times seem to show higher ‘yes’ outcome.
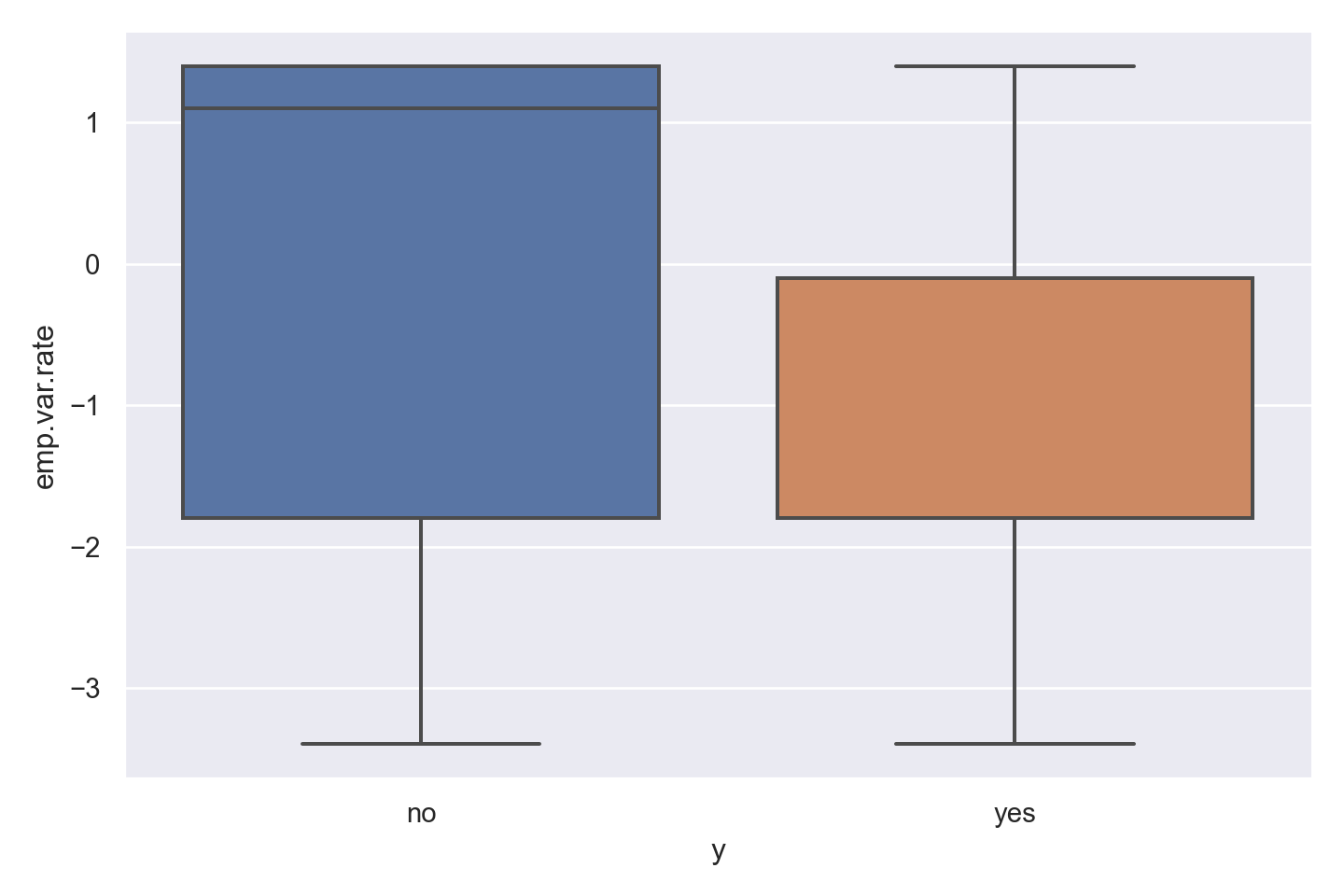
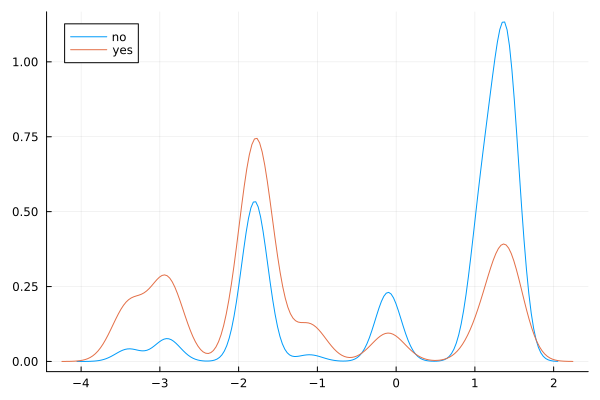
Observations
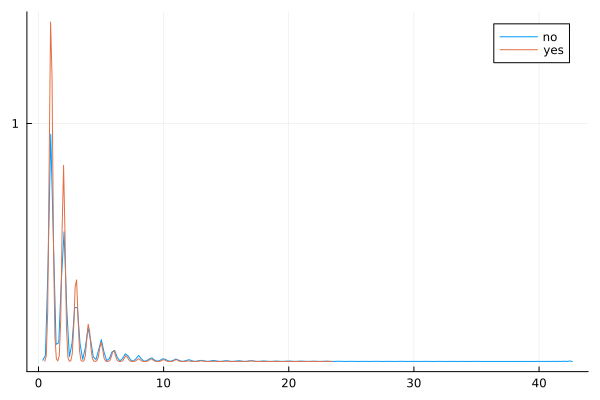
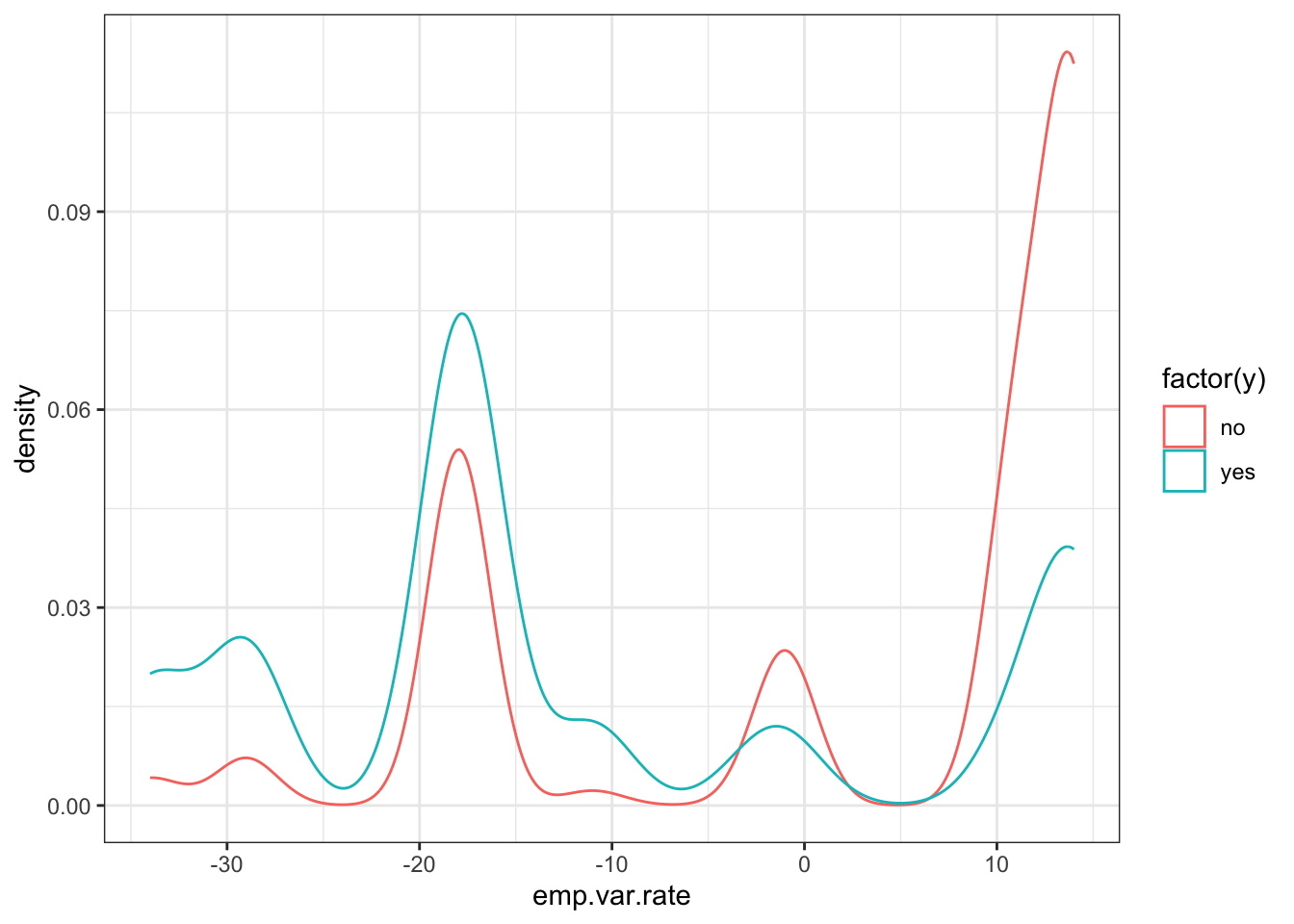
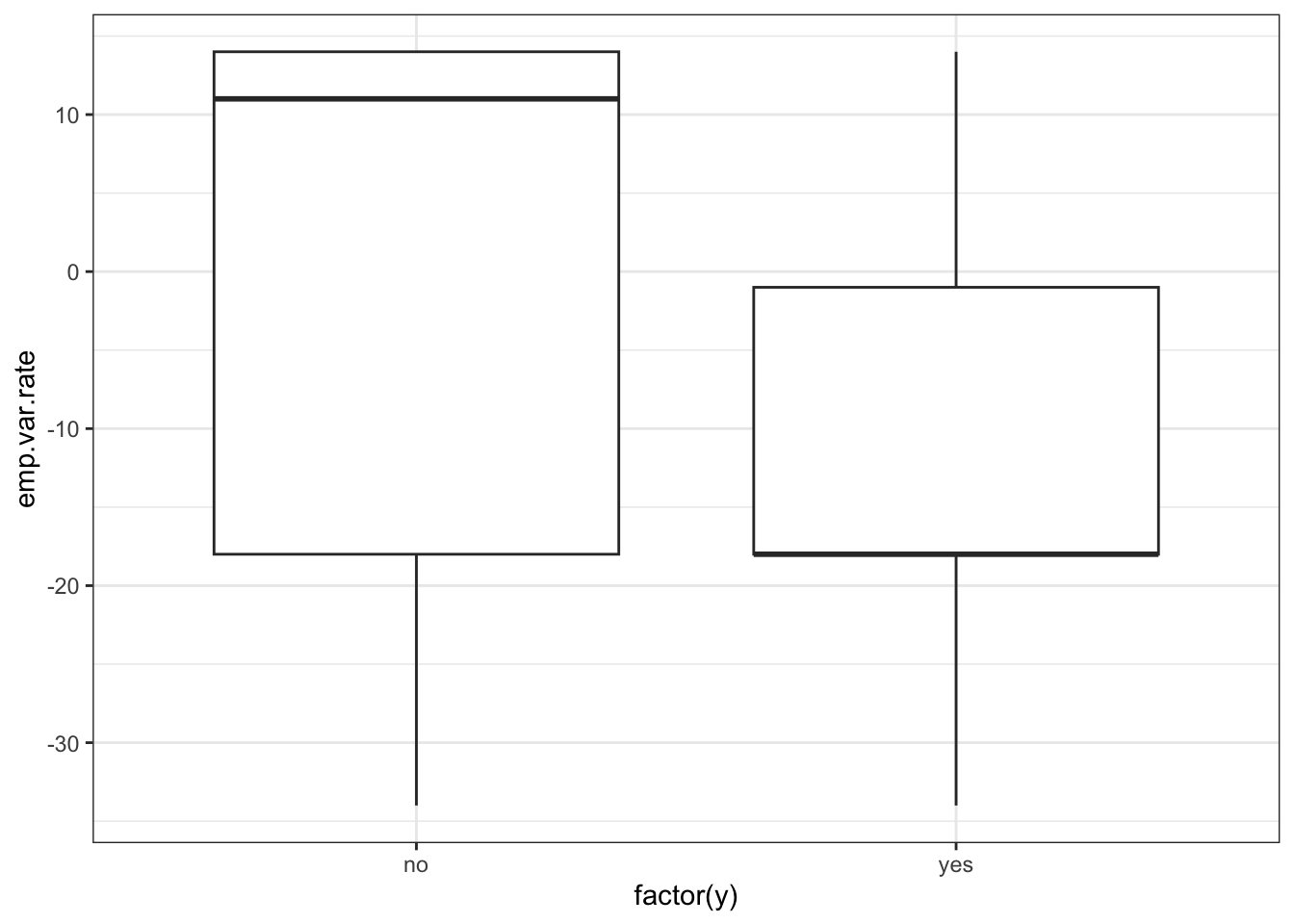
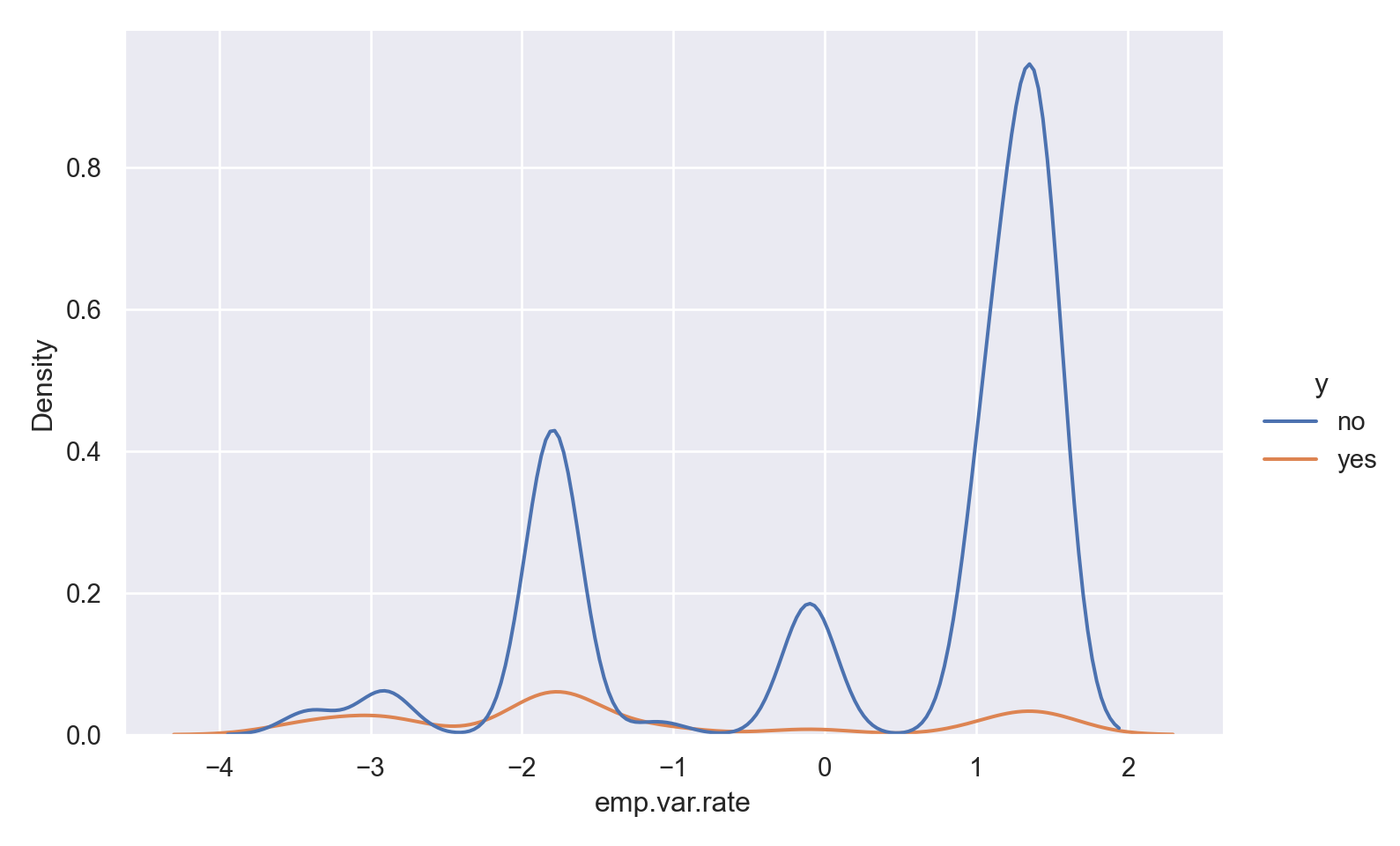
There is a striking association between employment variation rate and response - ‘yes’ outcomes show a much lower variation rate.
There is a multi-modal pattern in the data.
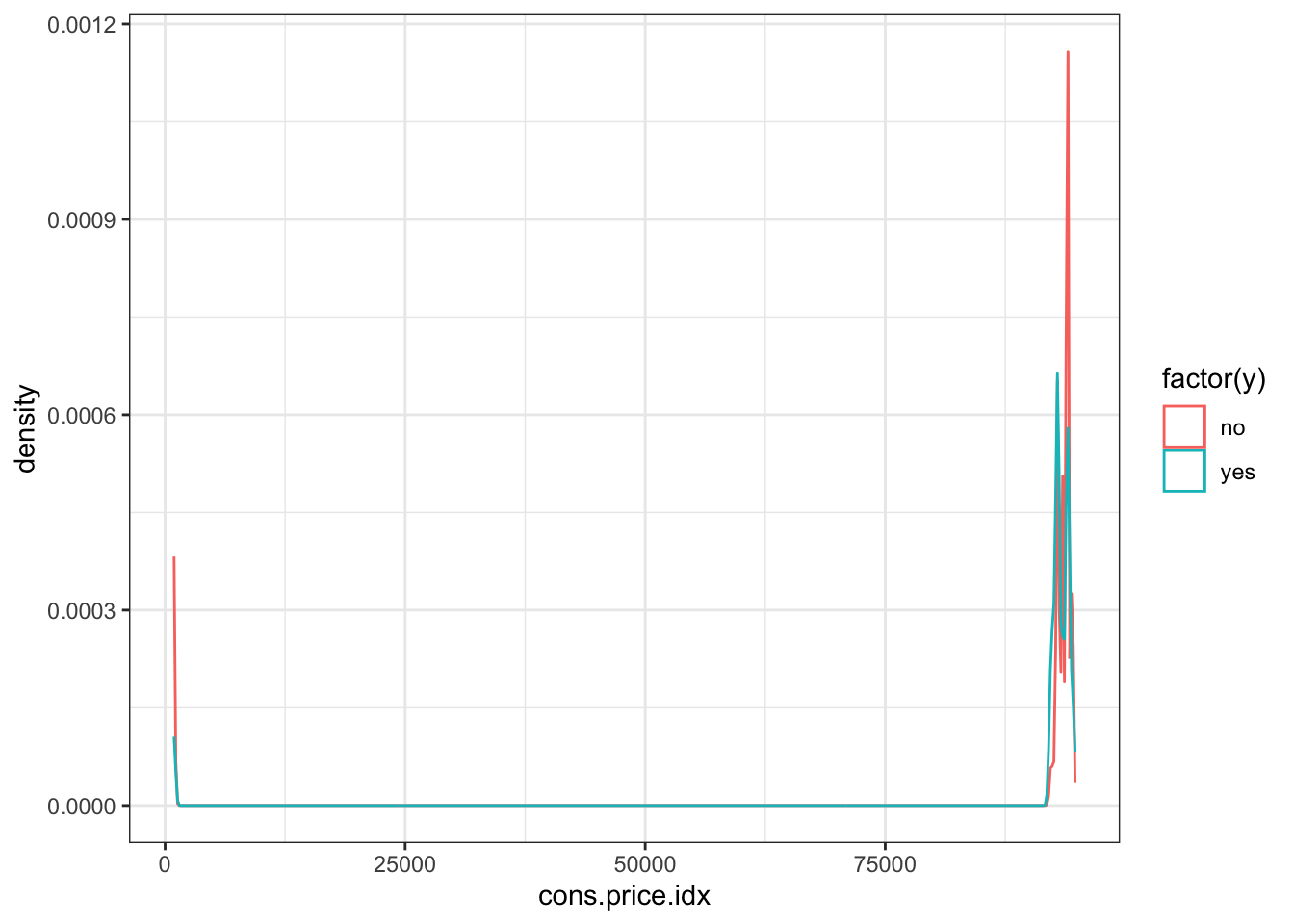
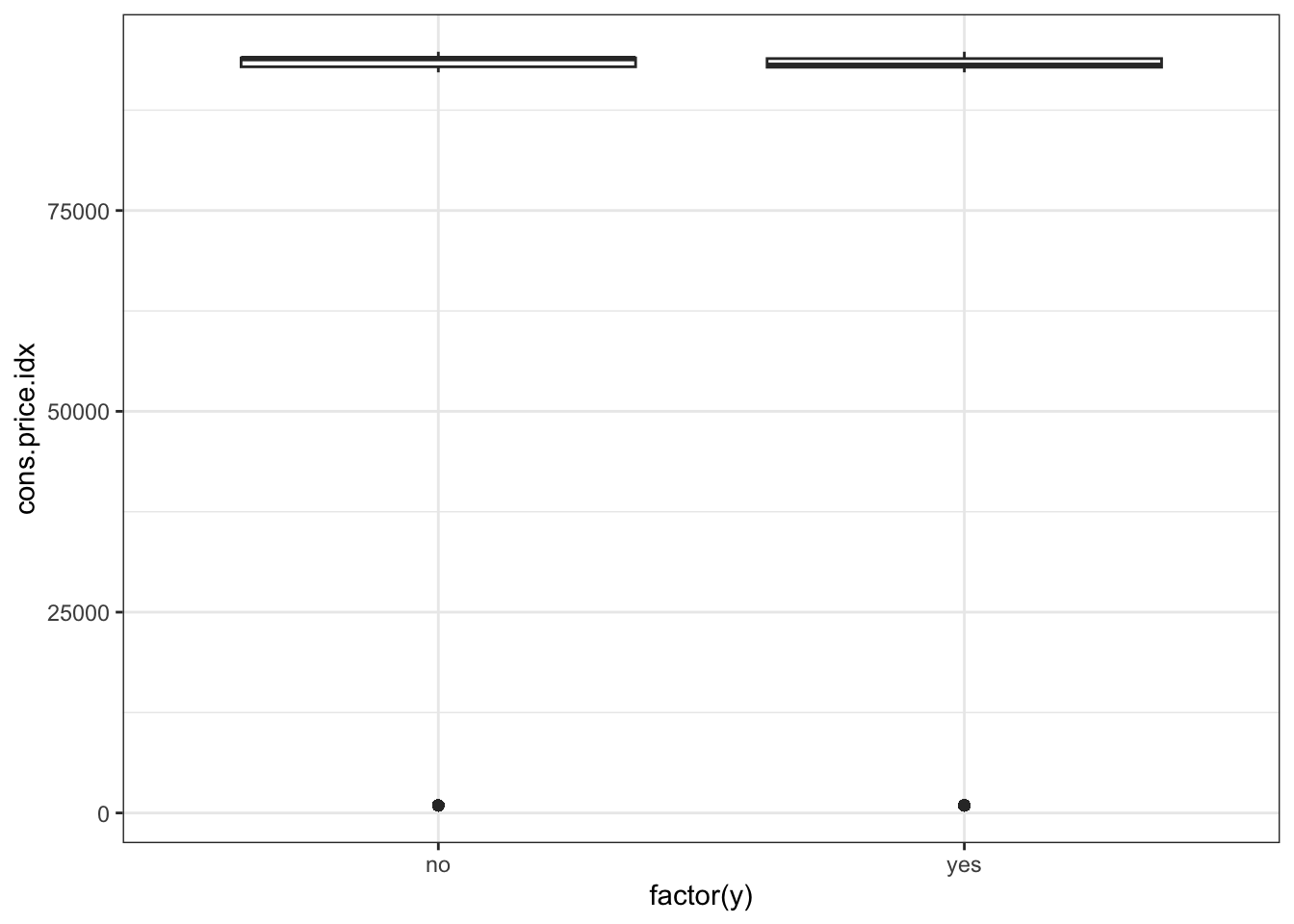
Observations
There is not much variation in the data,other than two outliers (perhaps data entry errors?)
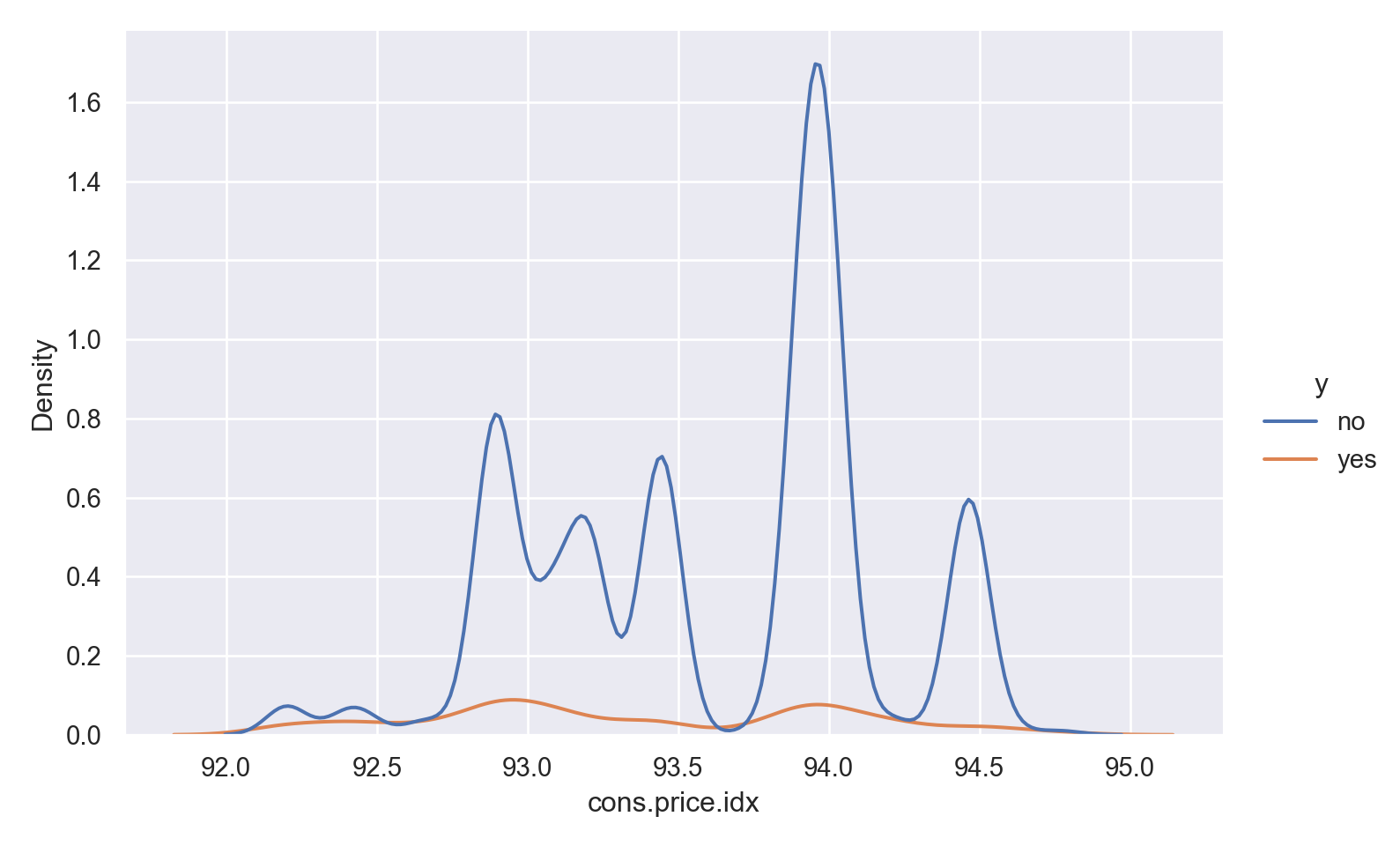
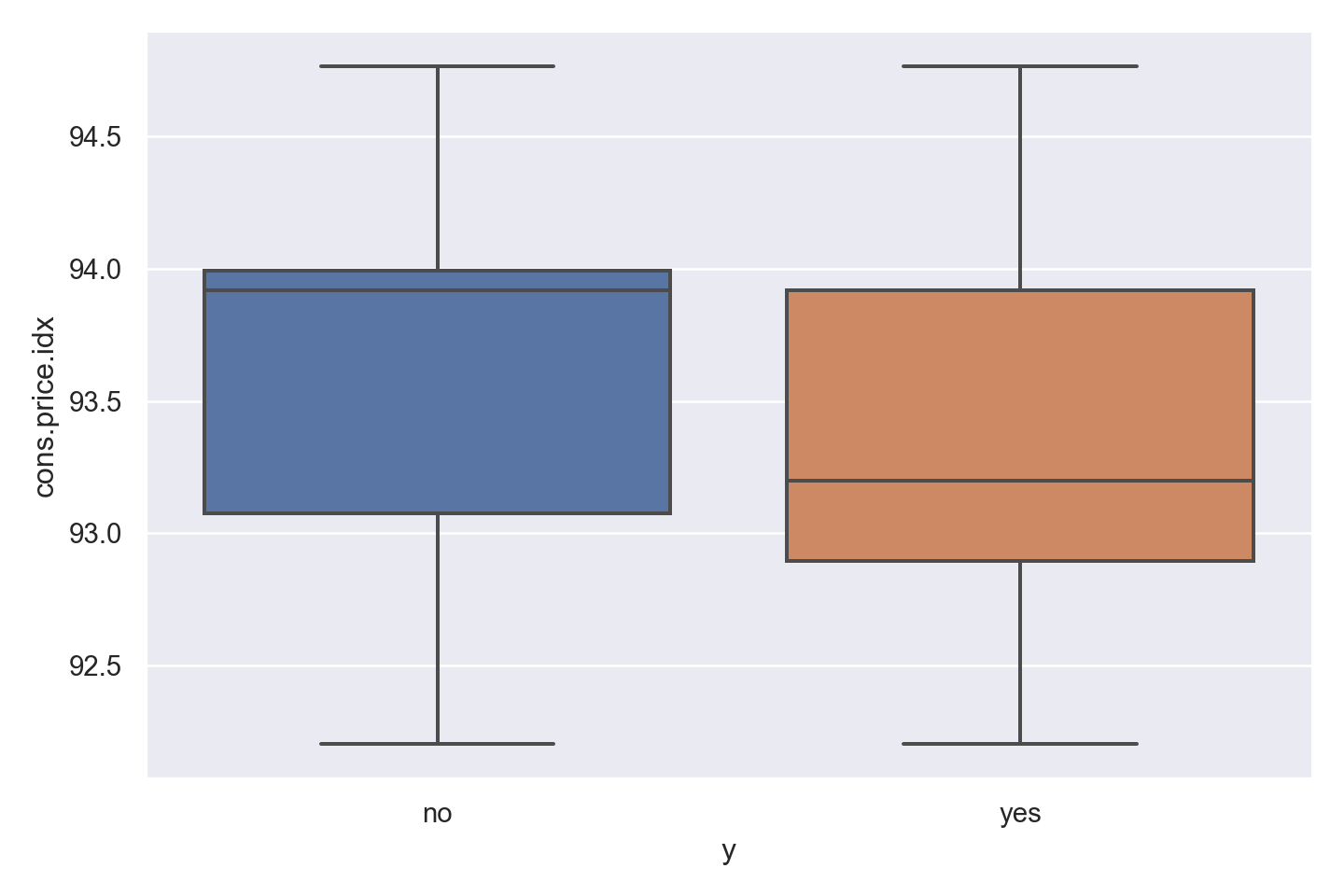
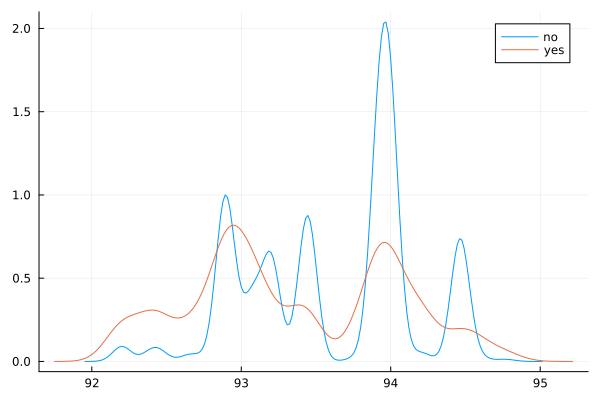
‘yes’ outcome is associated with a slightly lower price index.
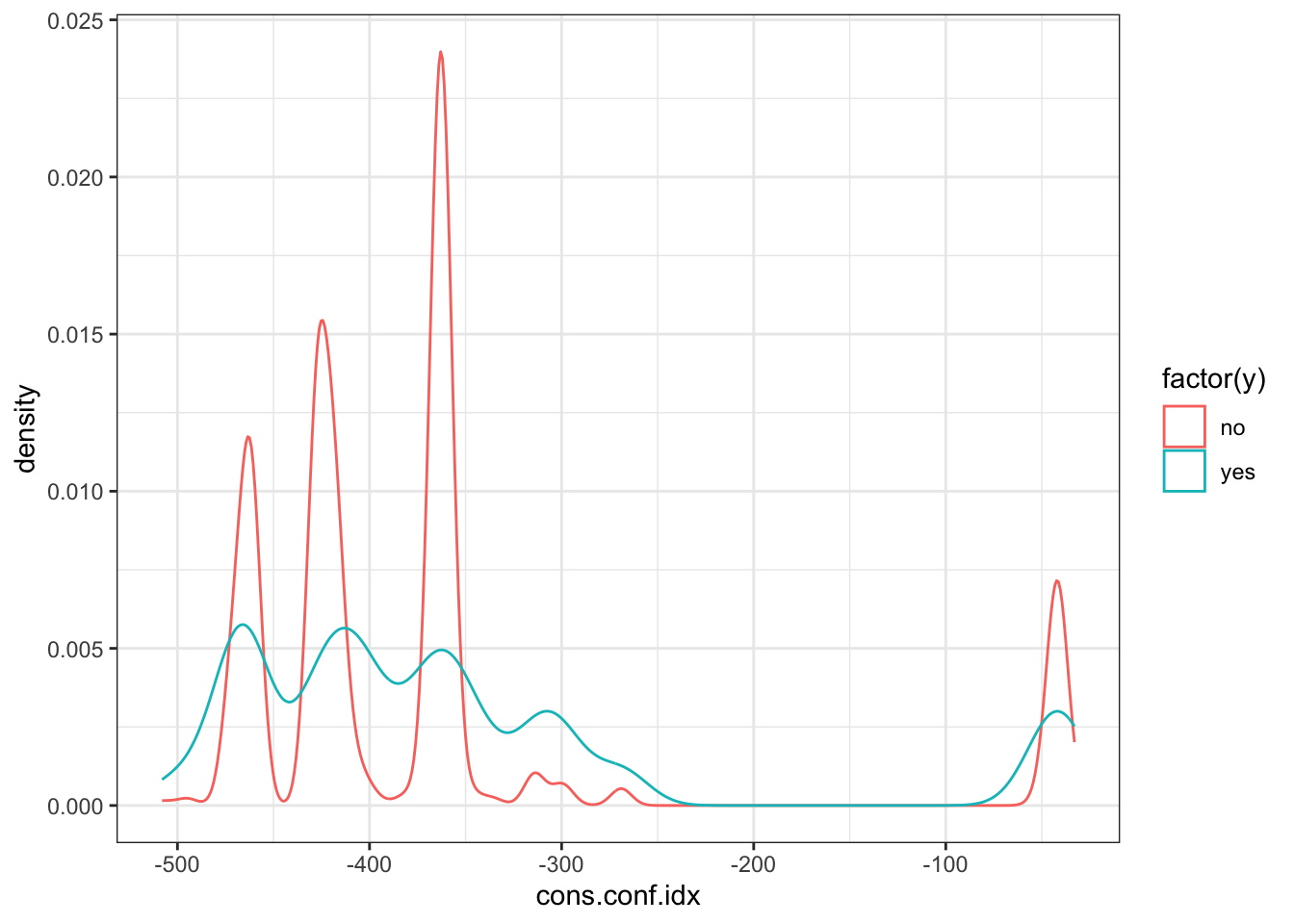
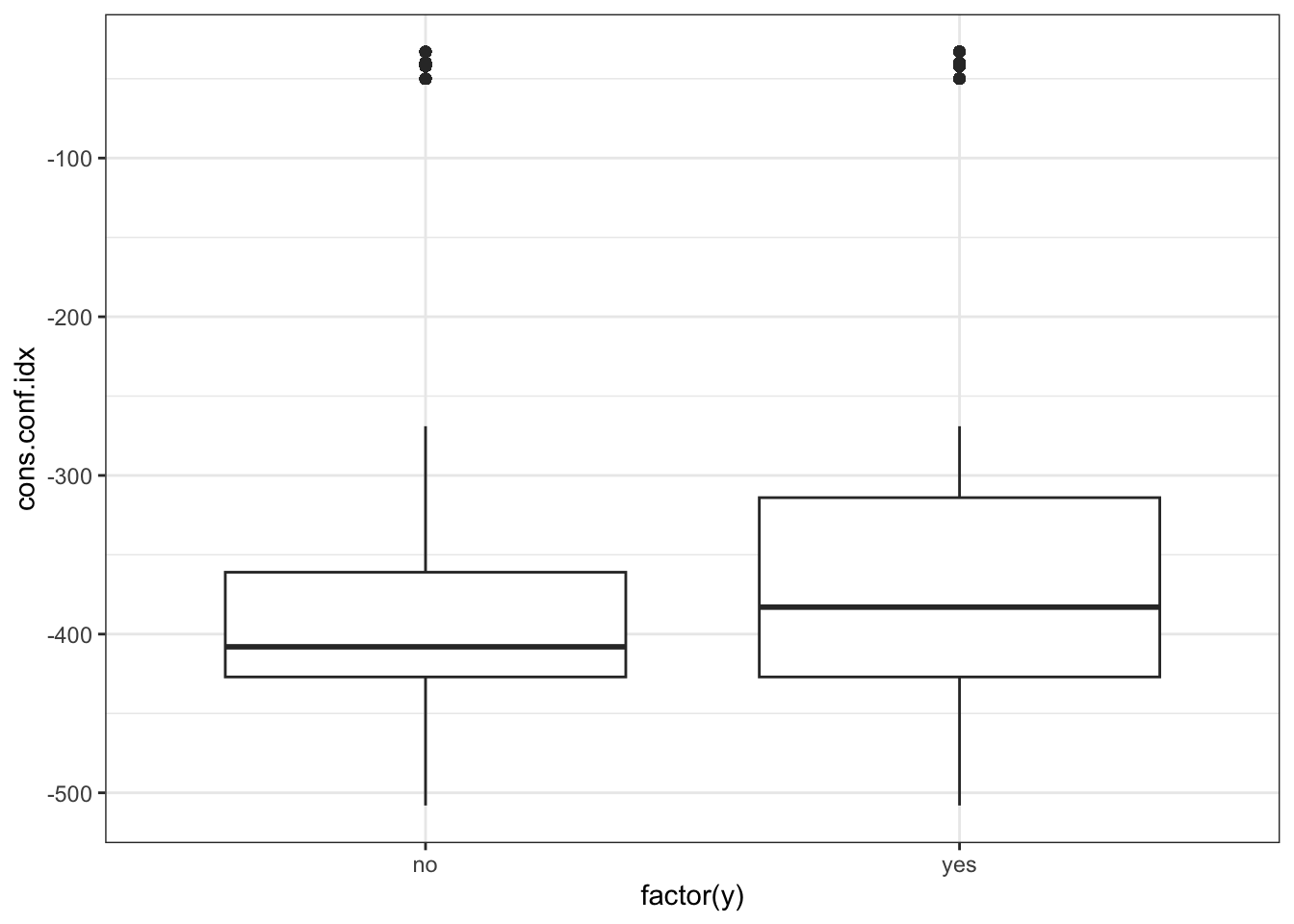
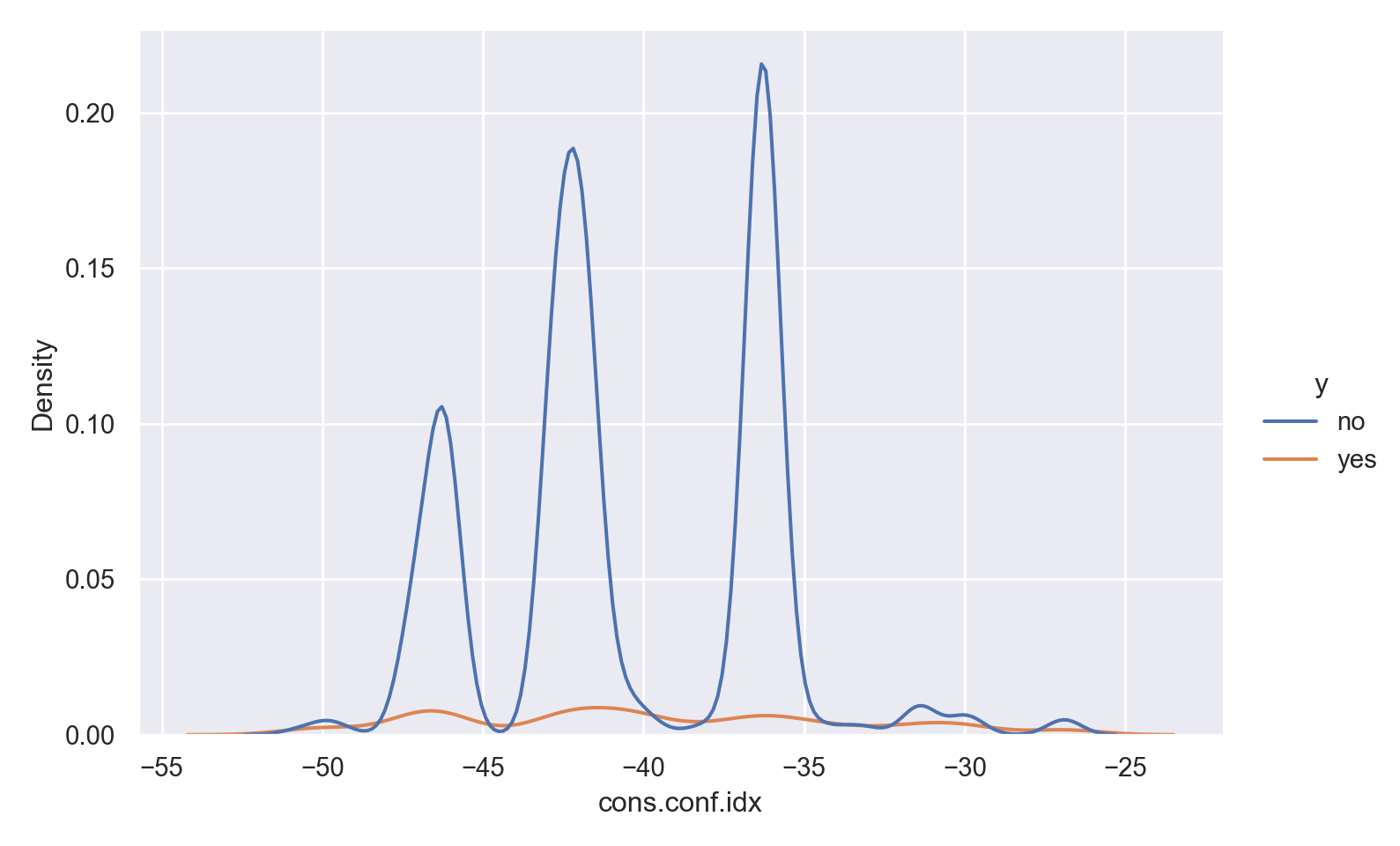
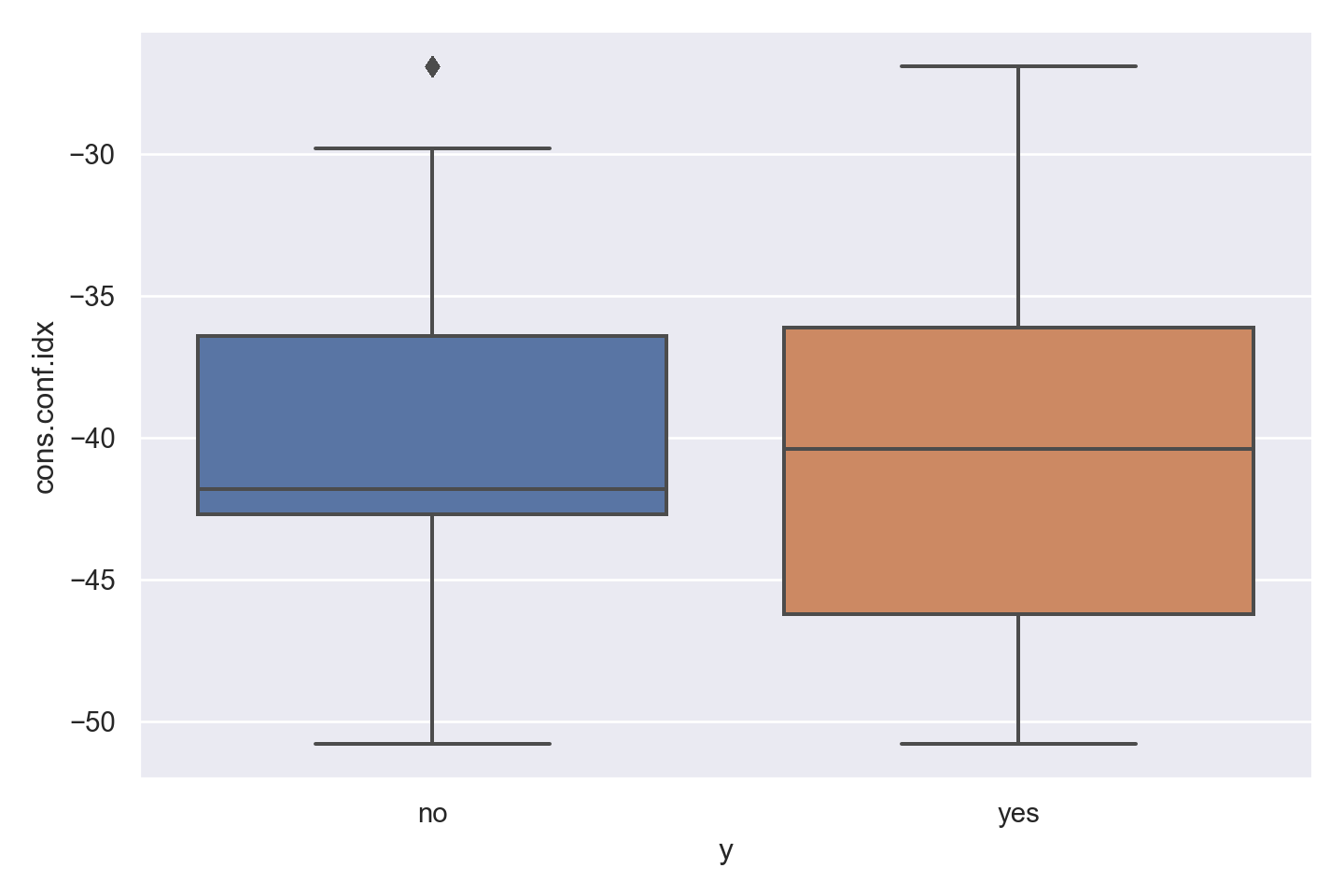
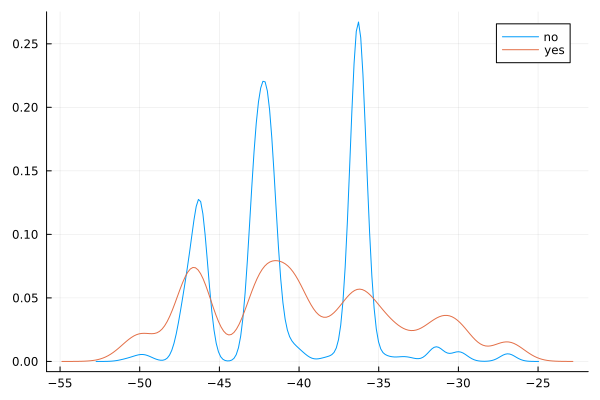
Observations
There is a strong association between confidence index and response - ‘yes’ outcomes show a higher index.
There is a multi-modal pattern in the data.
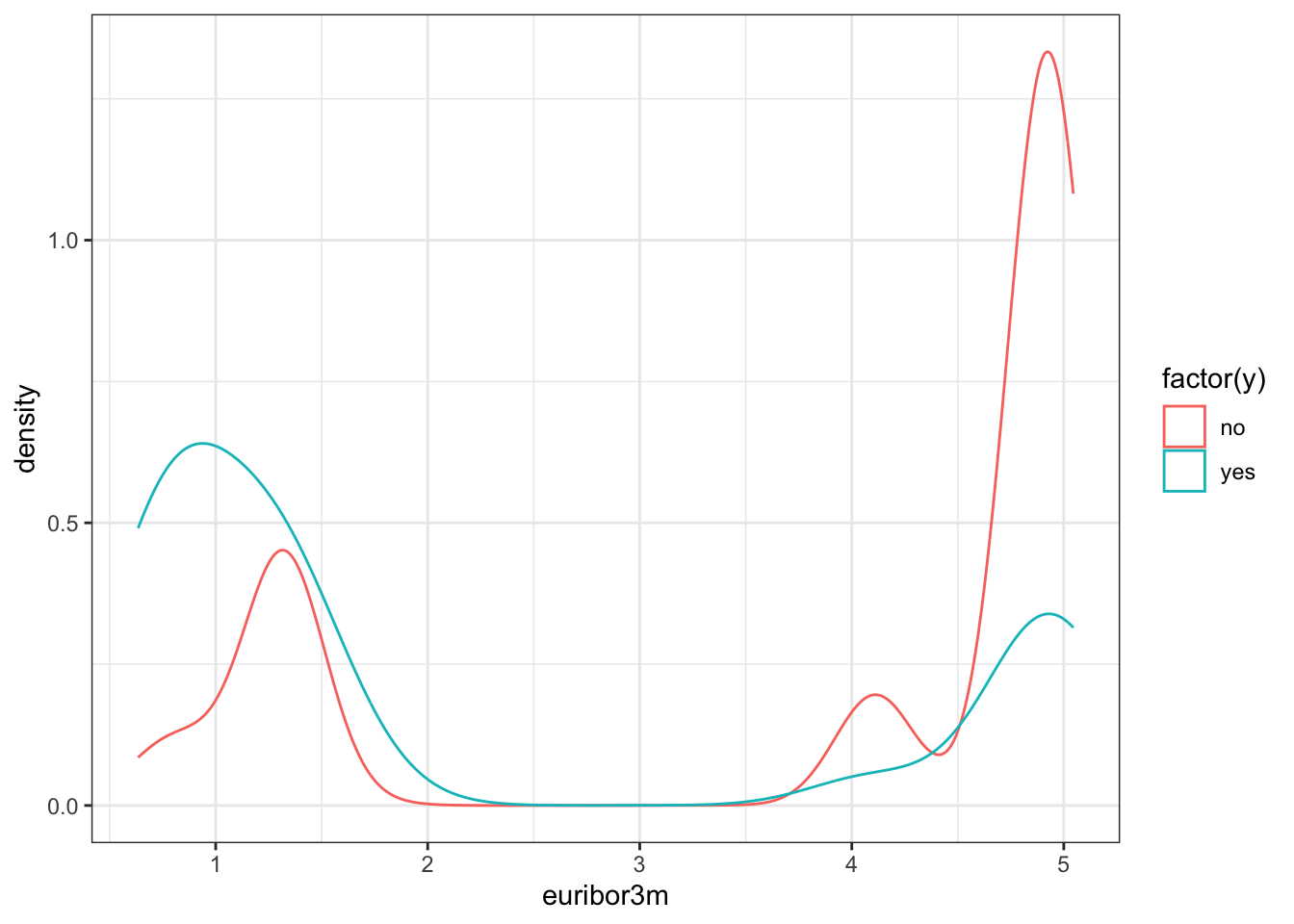
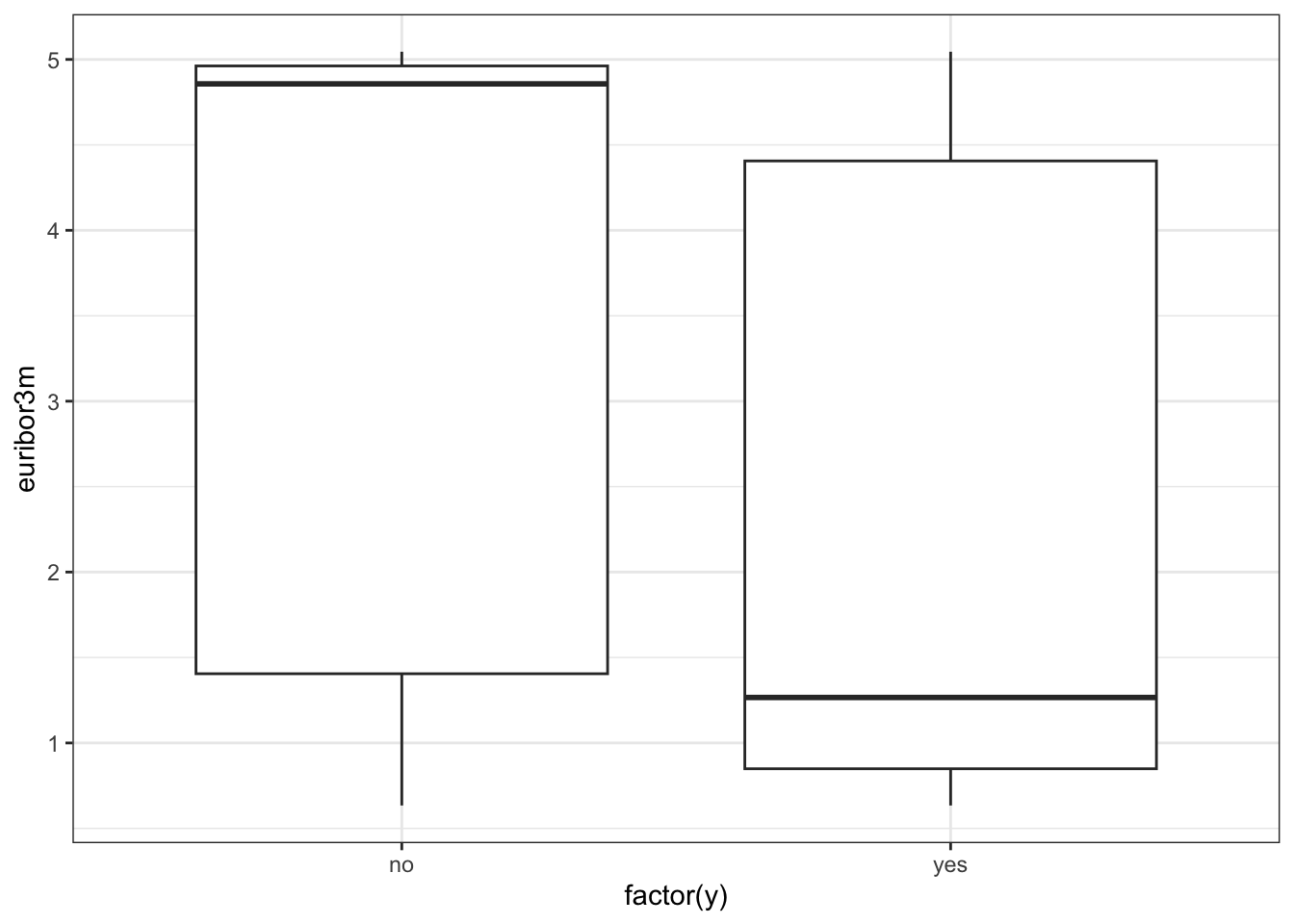
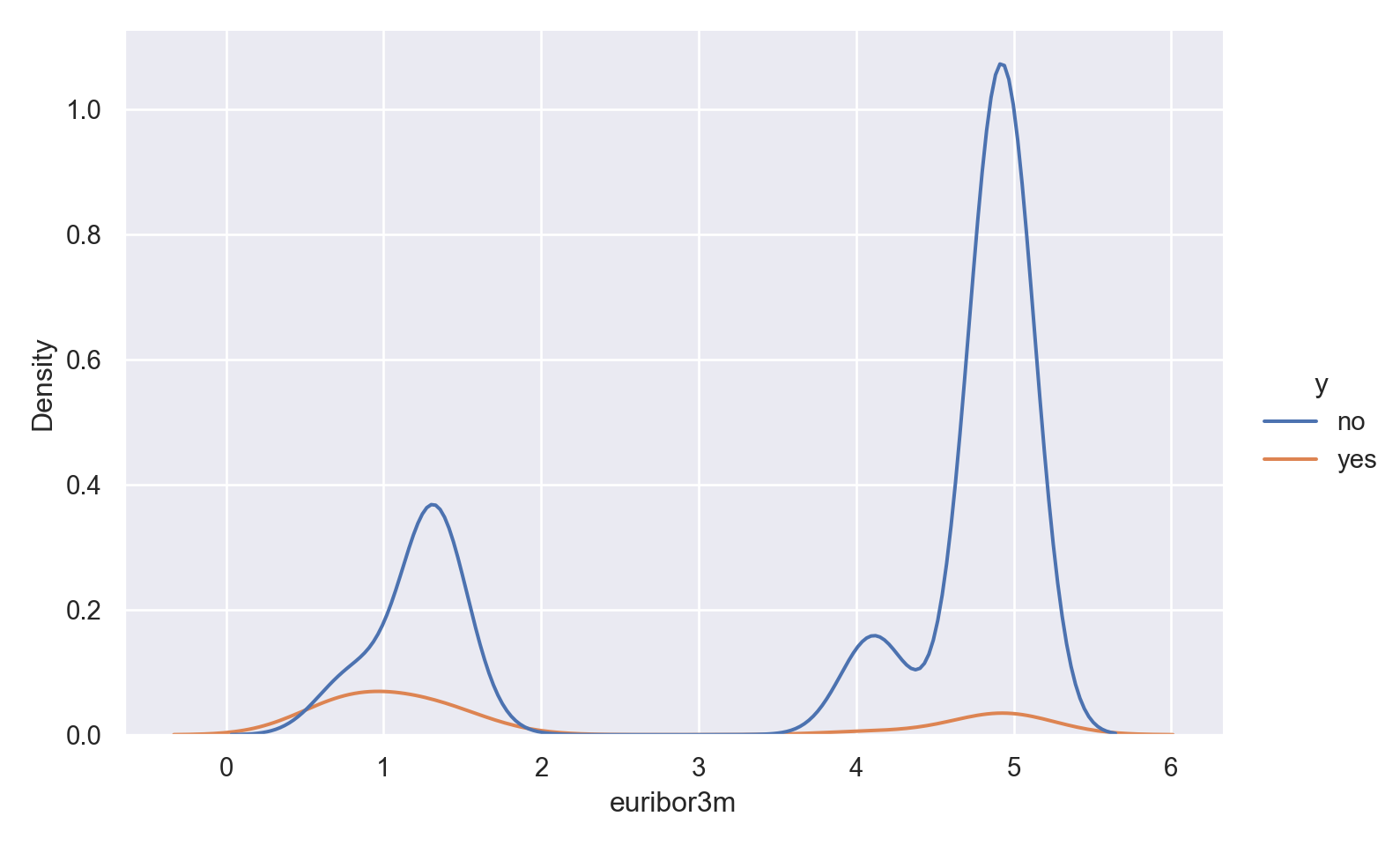
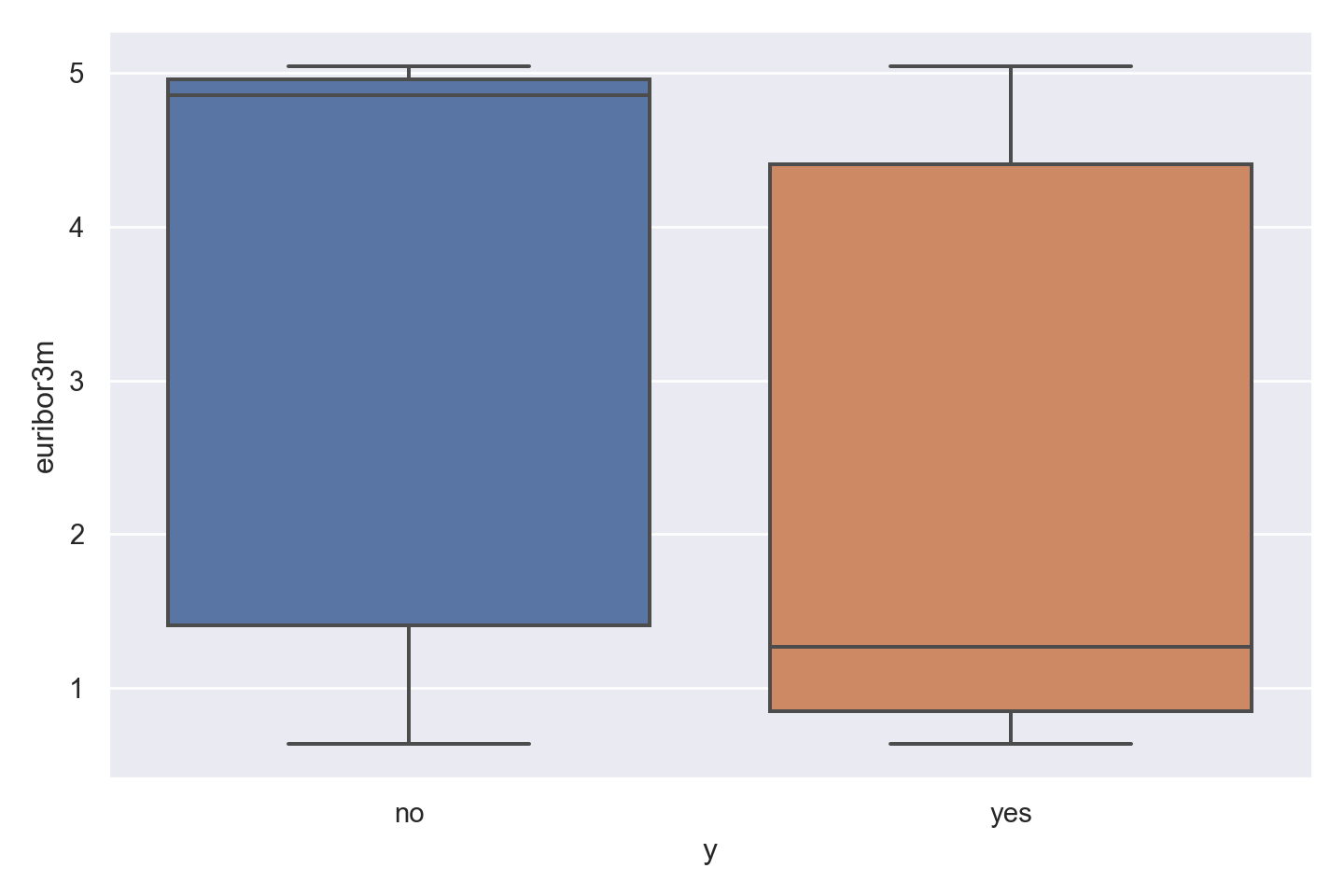
Observations
There is a striking association between employment euribor3m interest rate and response - ‘yes’ outcomes show a much lower interest rate.
There is a multi-modal pattern in the data, with more records for 1 and 5.
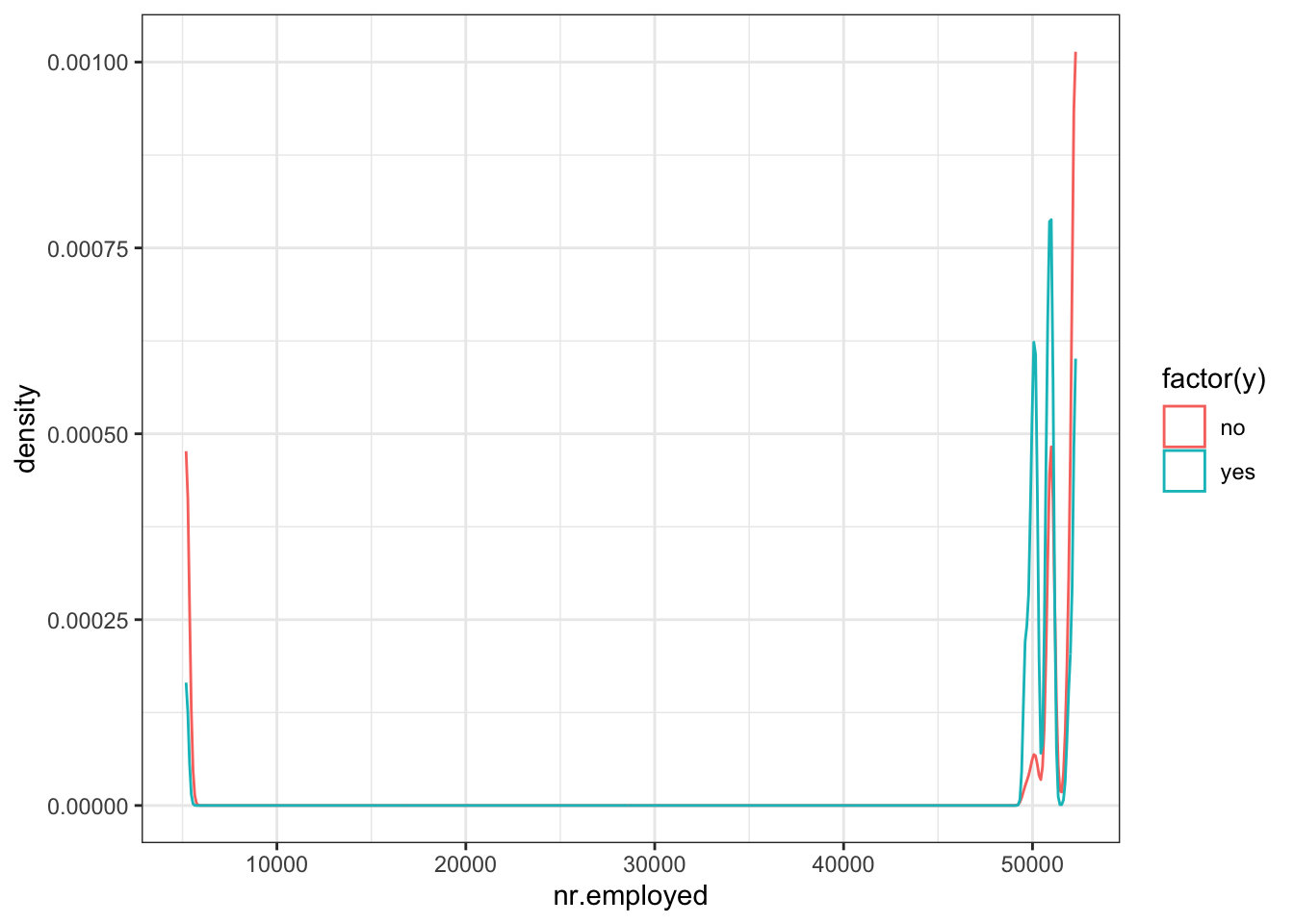
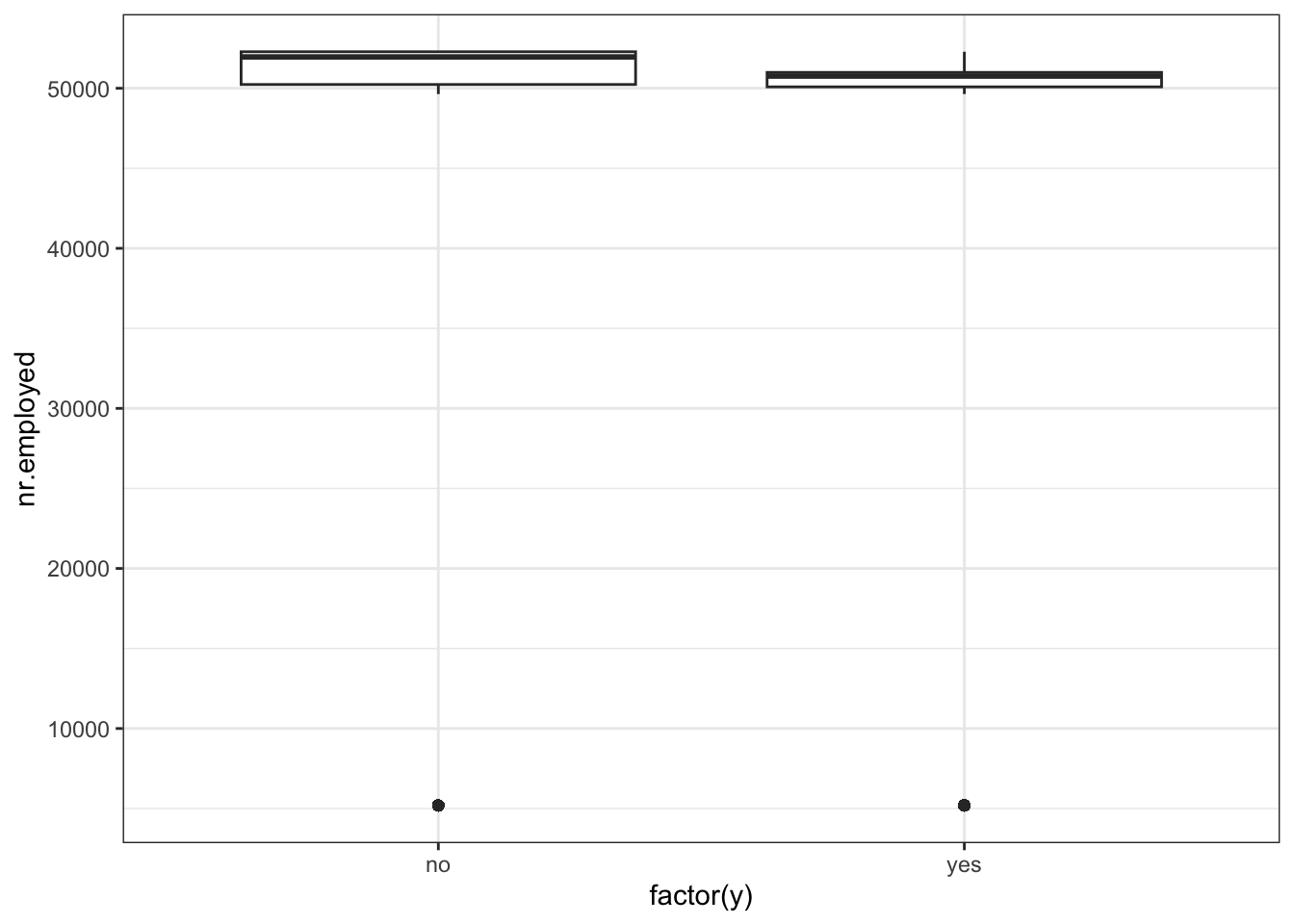
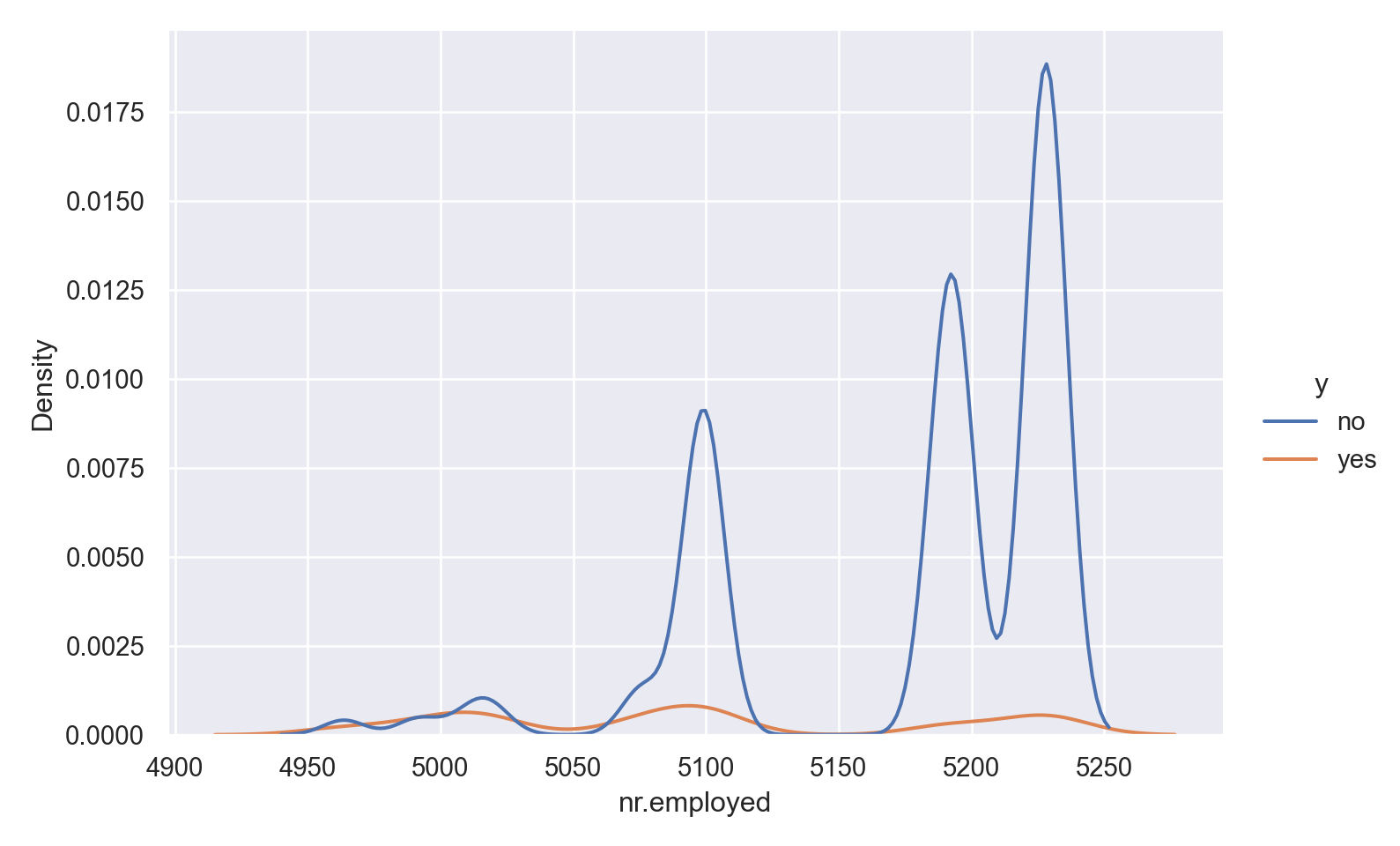
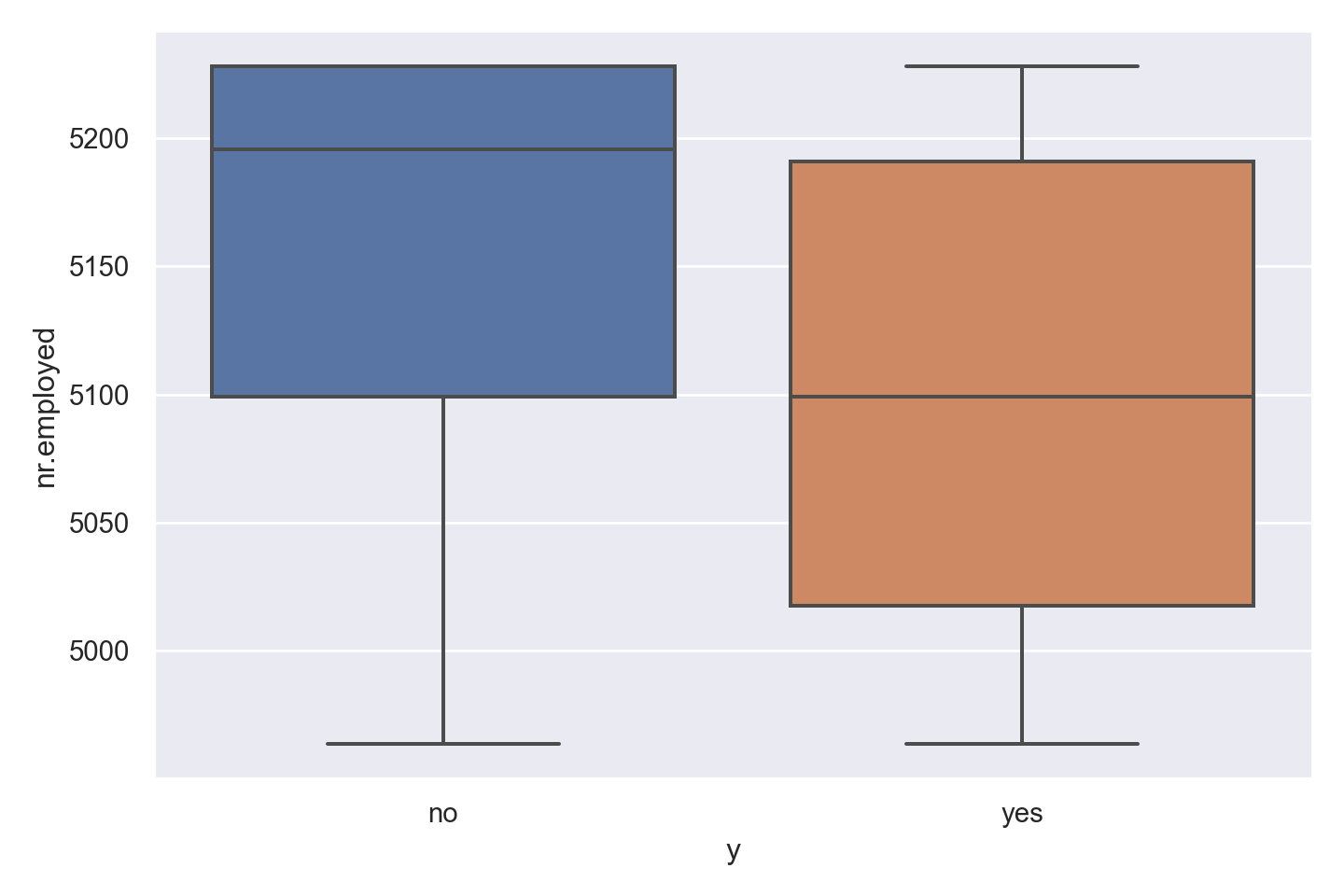
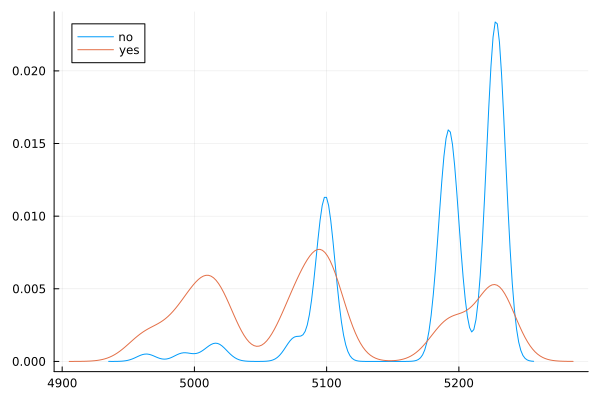
Observations
Curiously, ‘yes’ outcome is associated with a lower employment number.
There are two outliers in the data.
Categorical Attributes
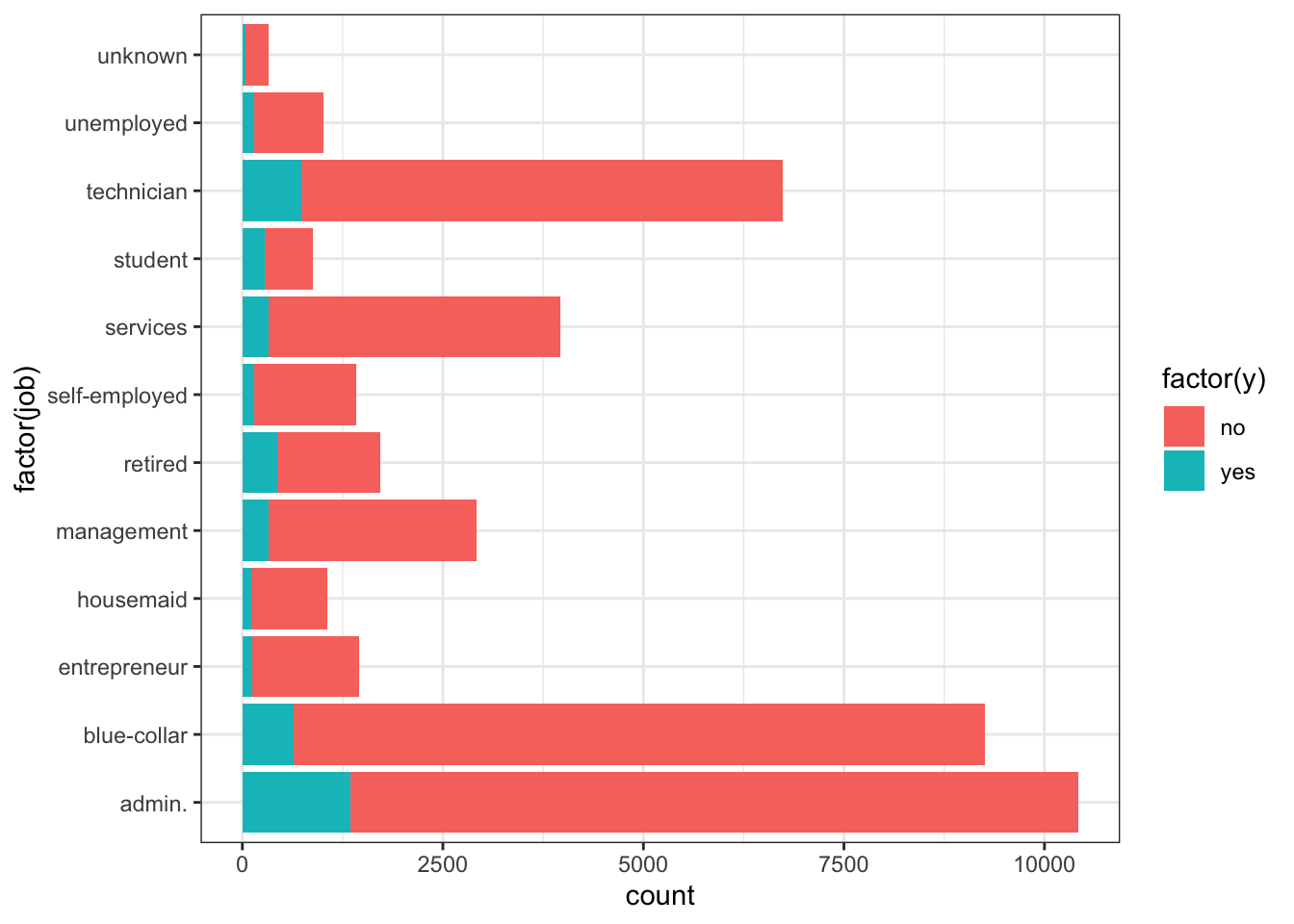
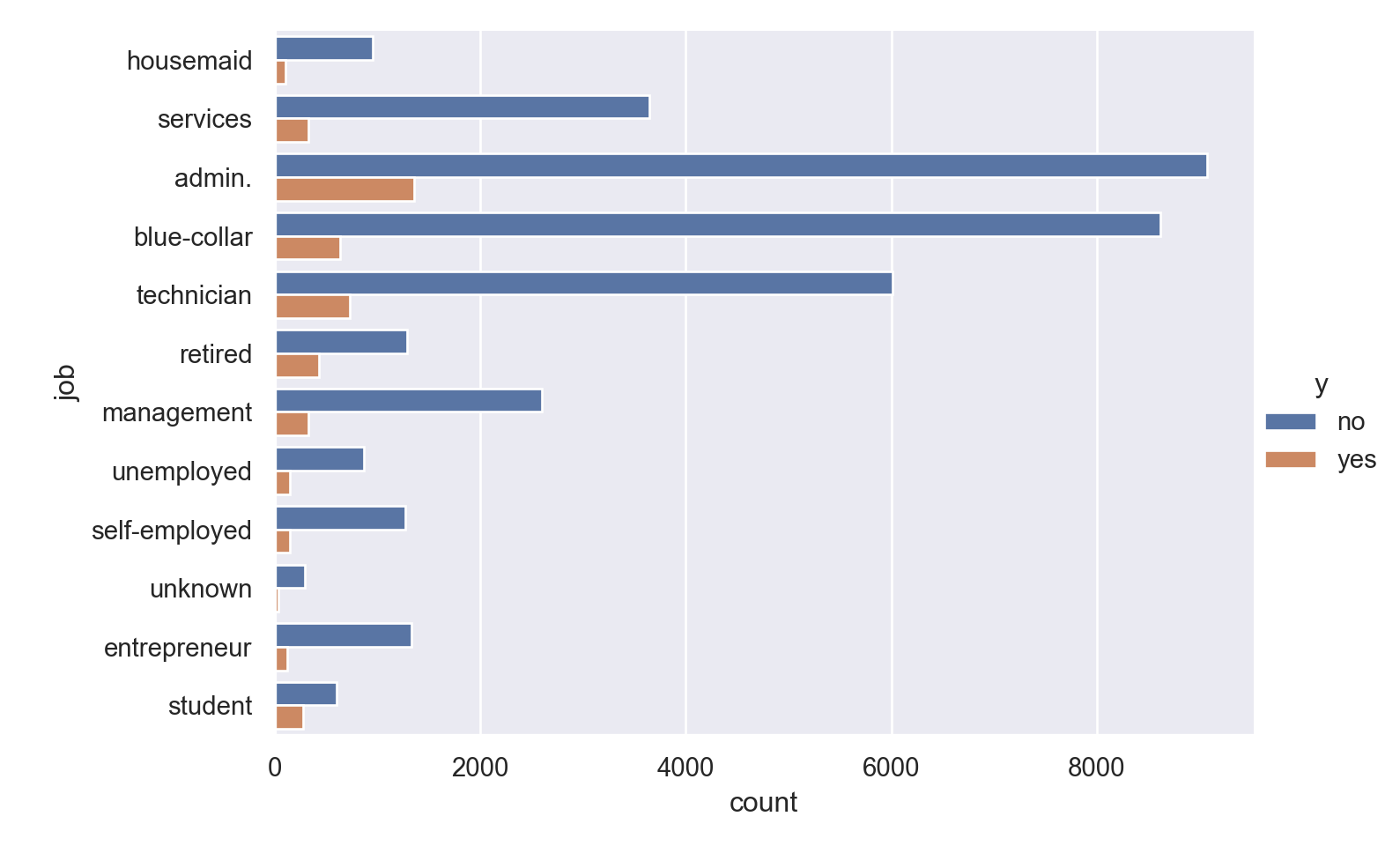
Observations
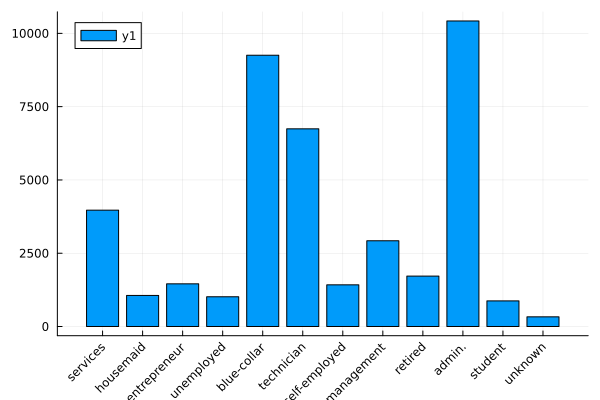
admin, blue-collar and technicians make up the majority of the people called.
There is higher percentage of yes outcome for students and retired persons, but the overall proportion of these categories is low (without being insignificant)
Observations
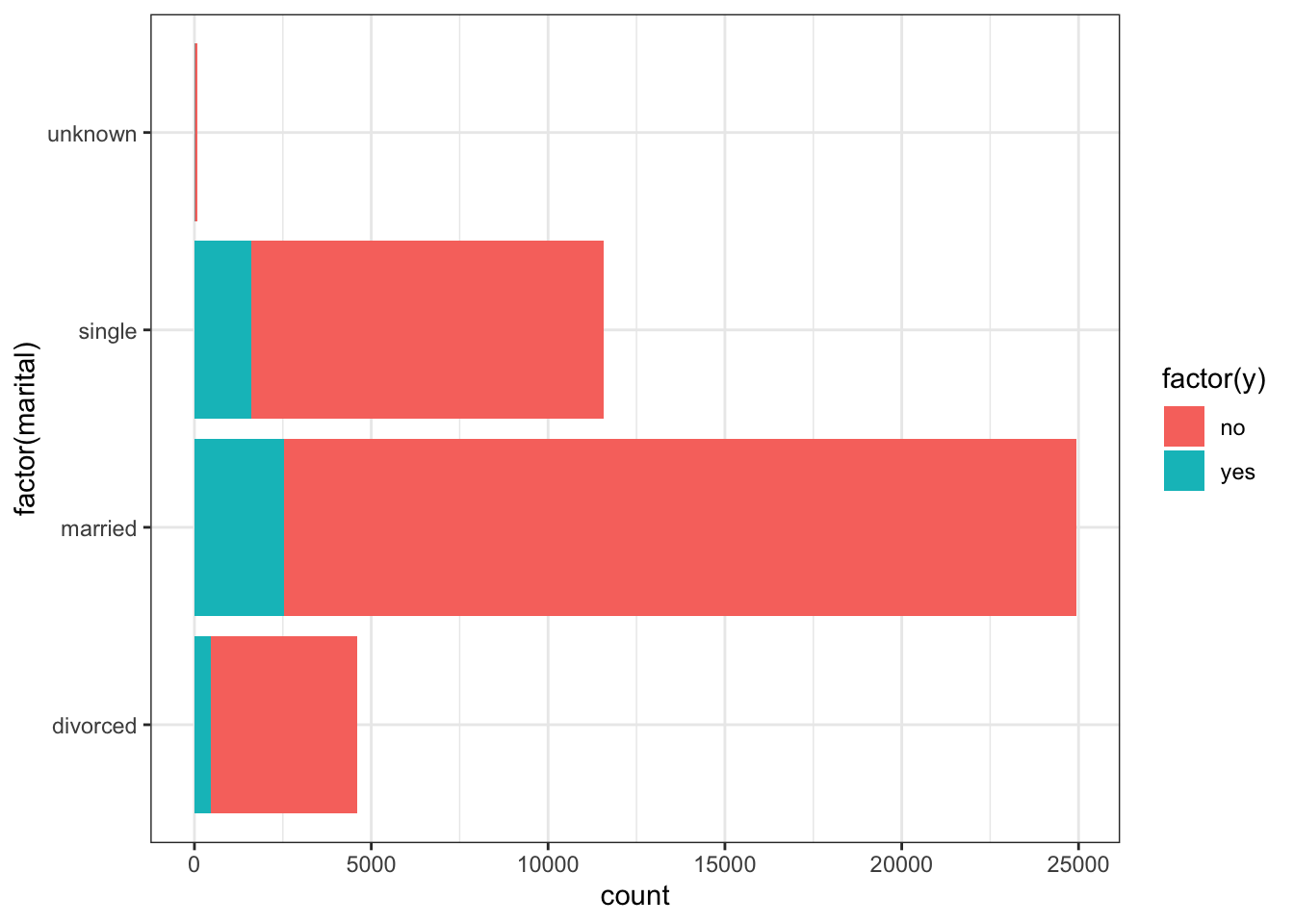
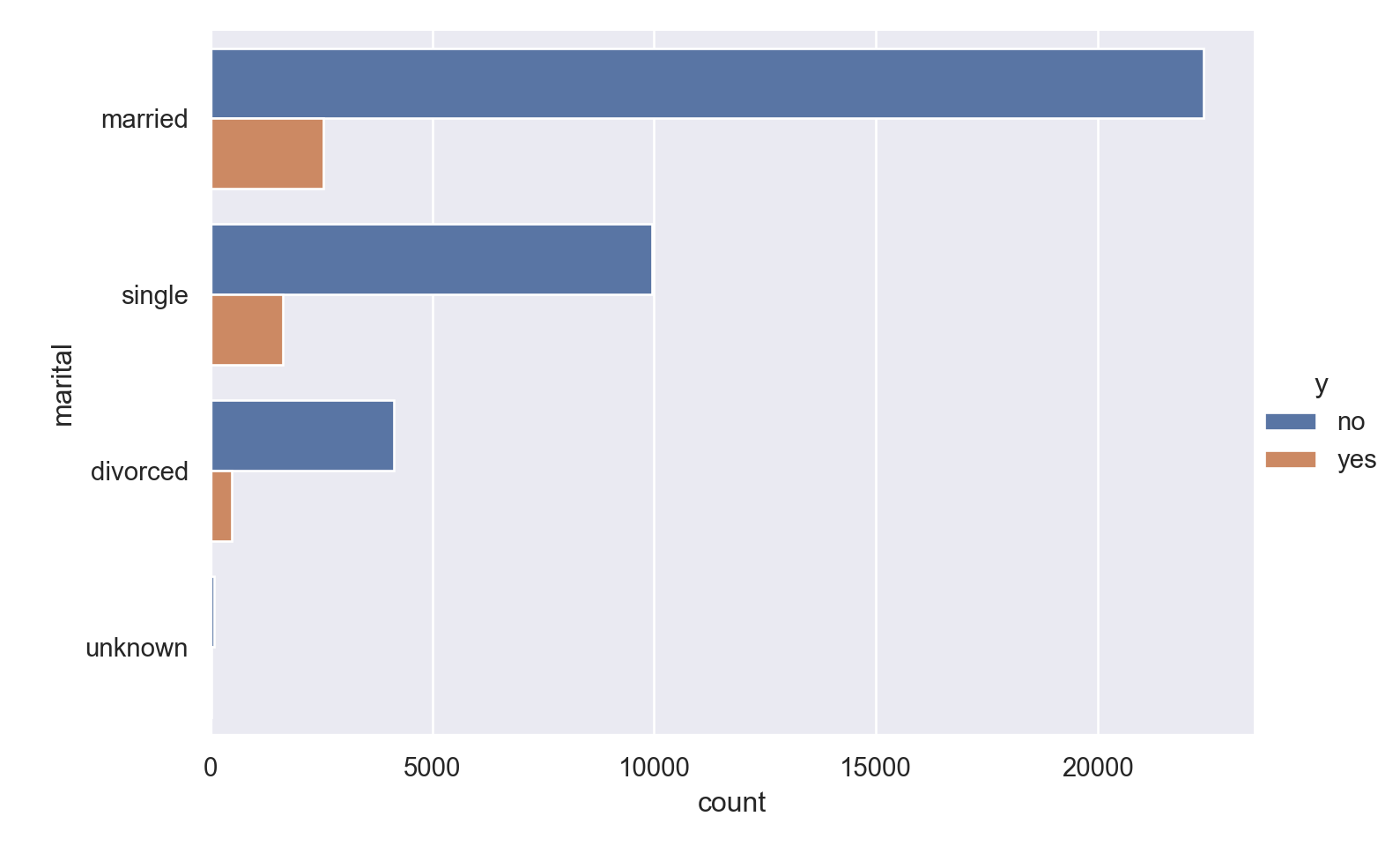
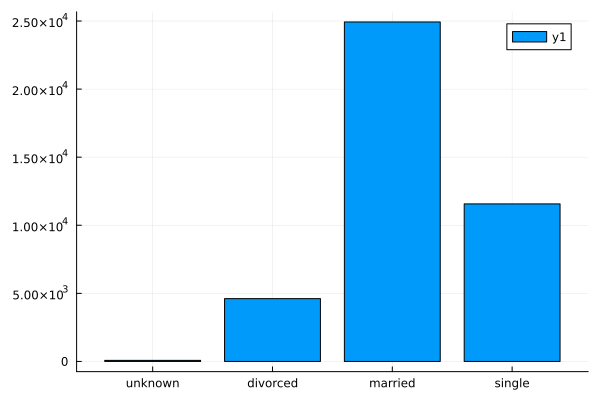
More of the people are married.
People who are single (and not divorced) have a higher proportion of ‘yes’ response.
Observations
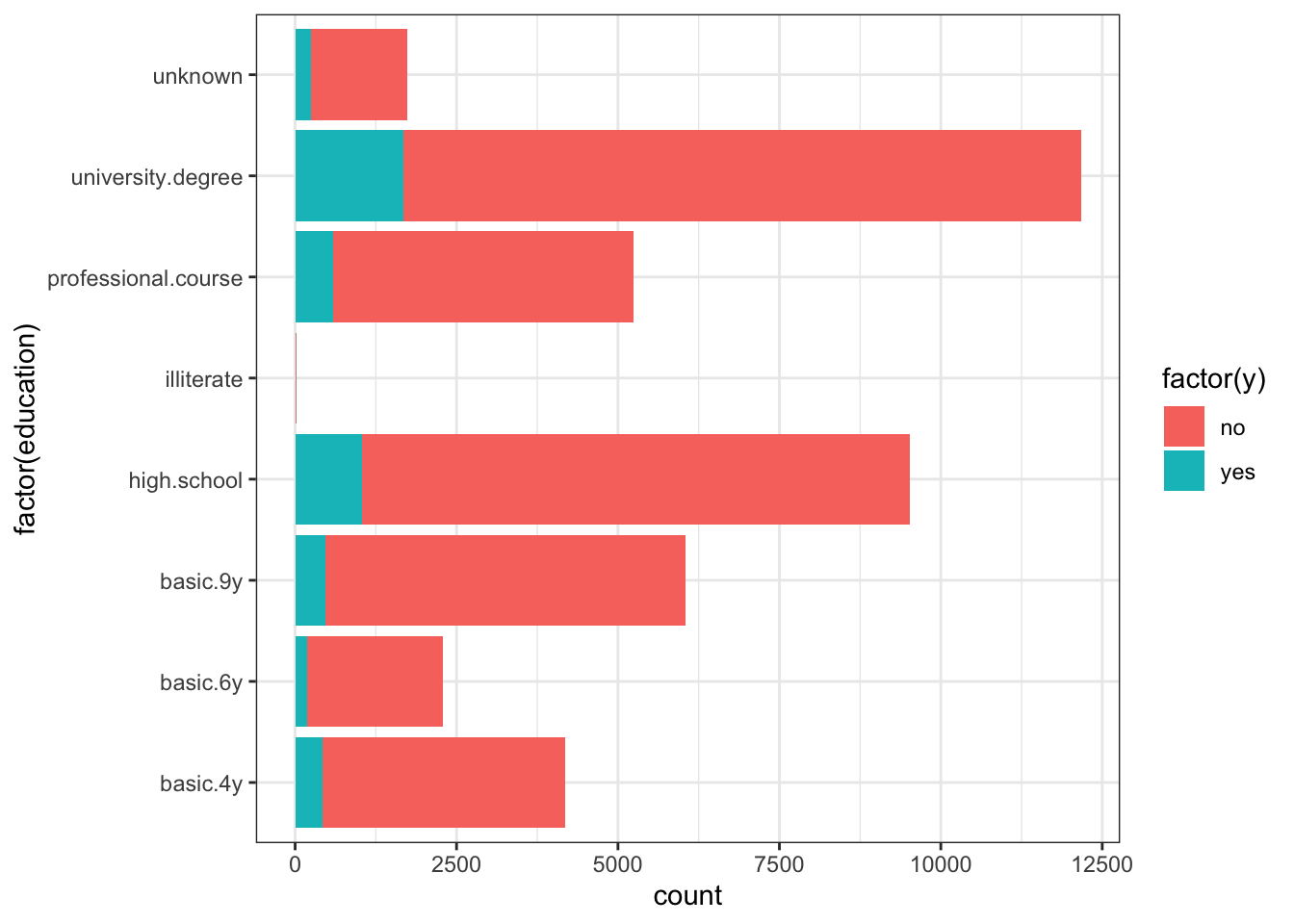
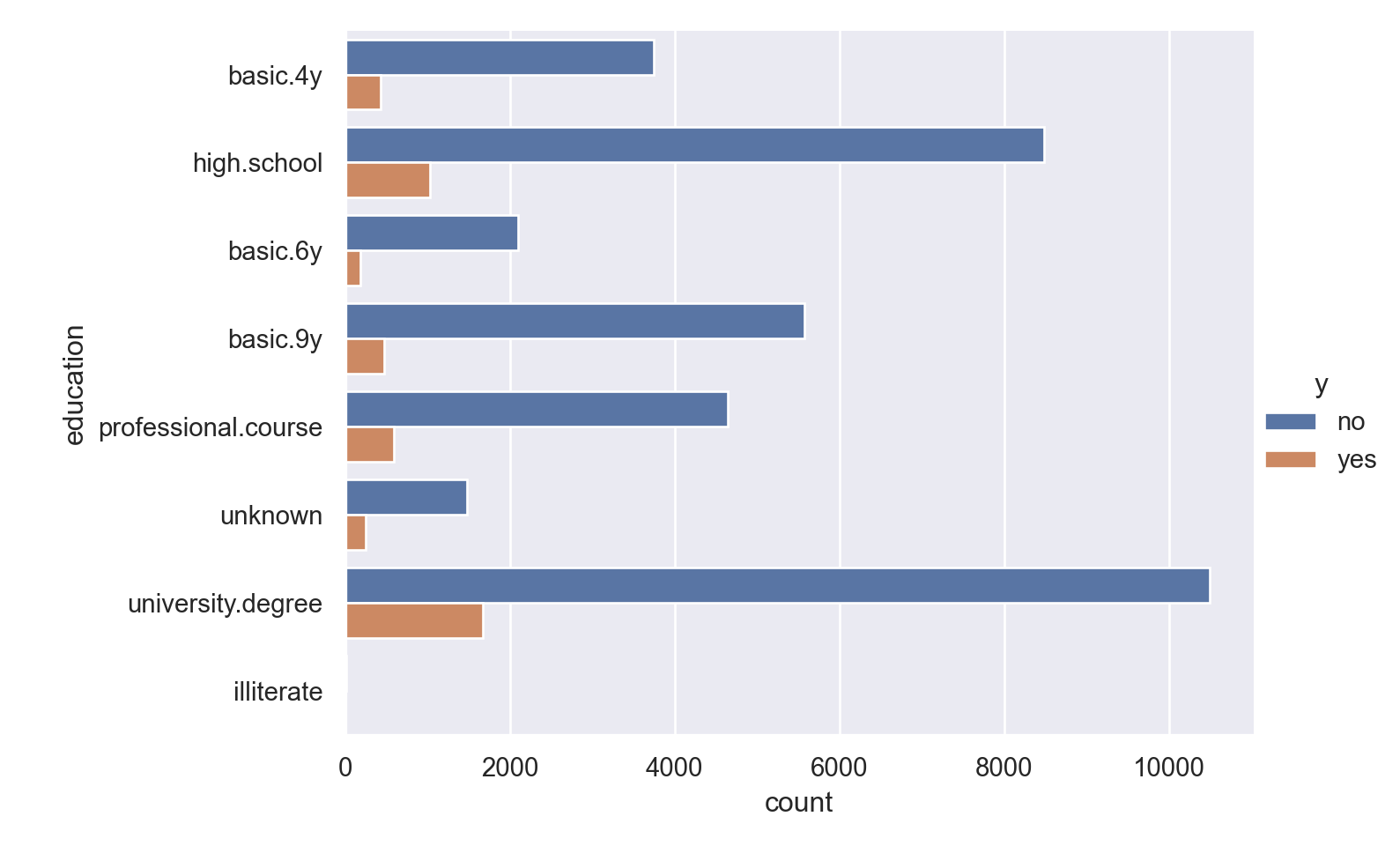
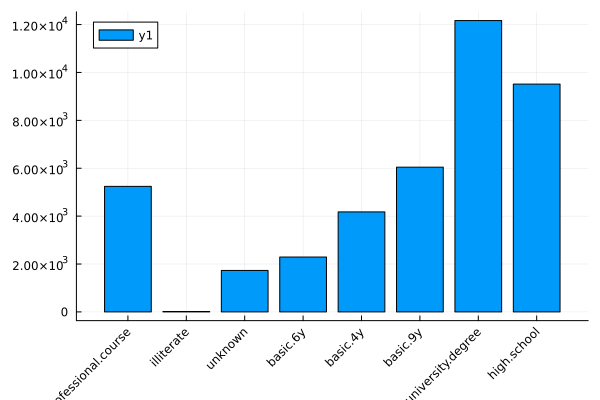
Most people called have 9 years or more education; many have a university degree.
Those with university degree show a slightly higher proportion of ‘yes’ outcome (confirmed by the numerical inspection).
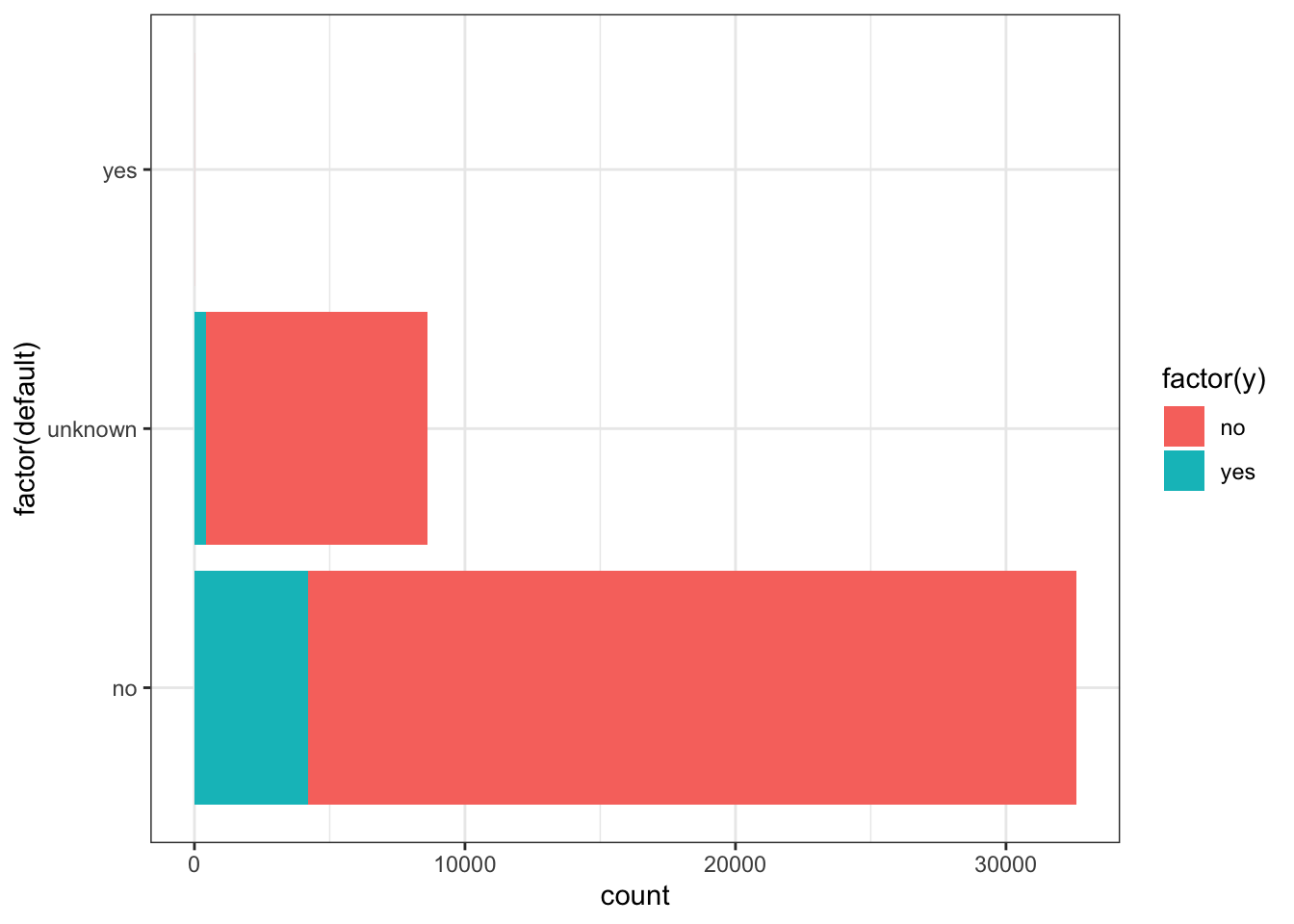
Observations
- A minuscule number of the people called have a loan default.
Observations
- Those contacted on cellular phones have a significantly higher possibility of subscribing to the deposit.
Observations
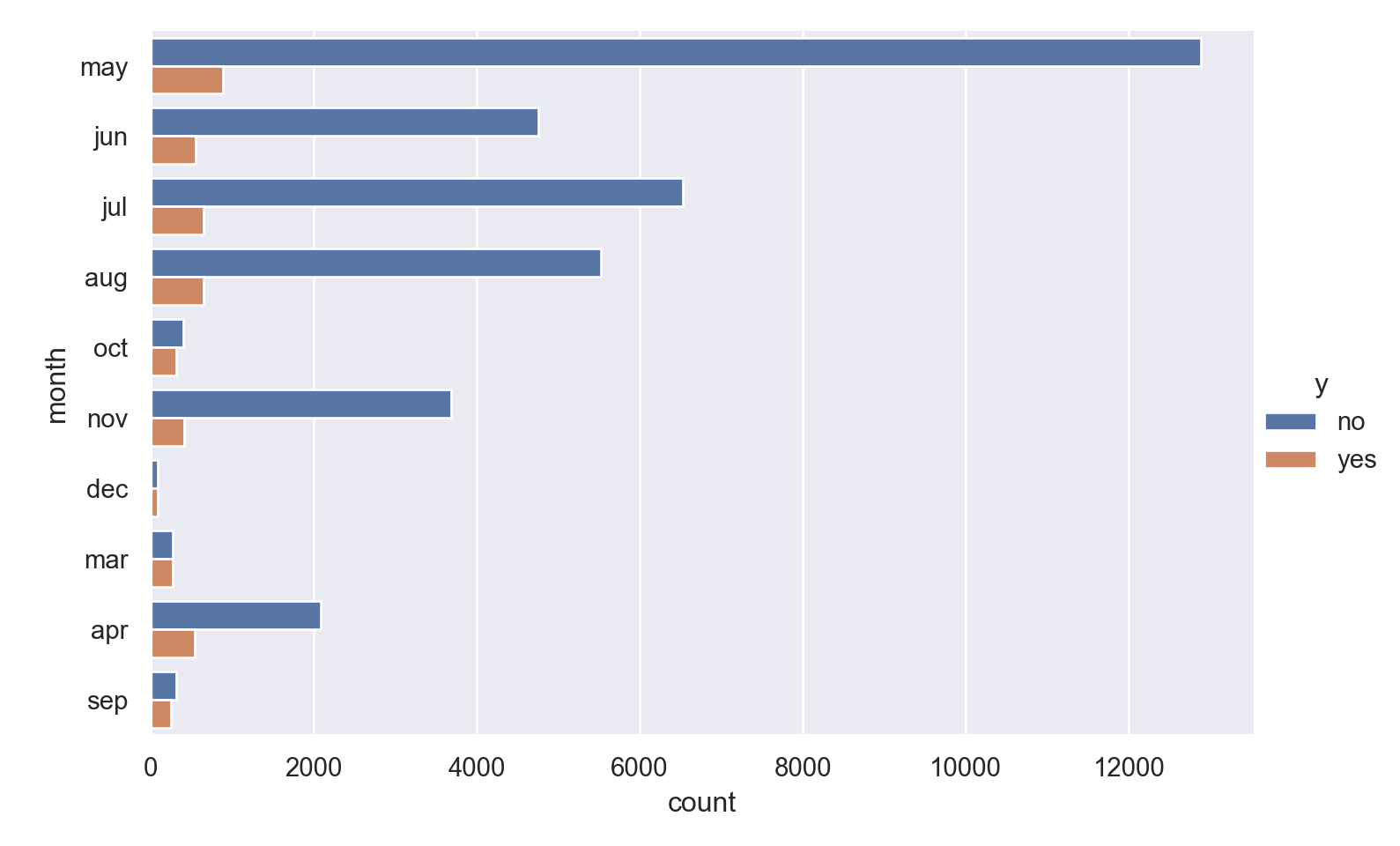
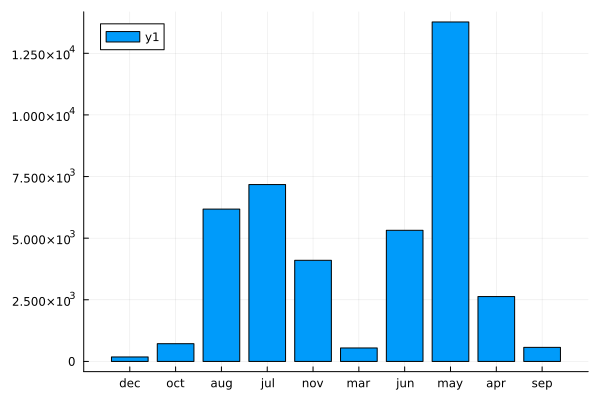
Most calls are placed in May.
The months where there were much fewer calls have a much larger chance of subscribing for the loan.
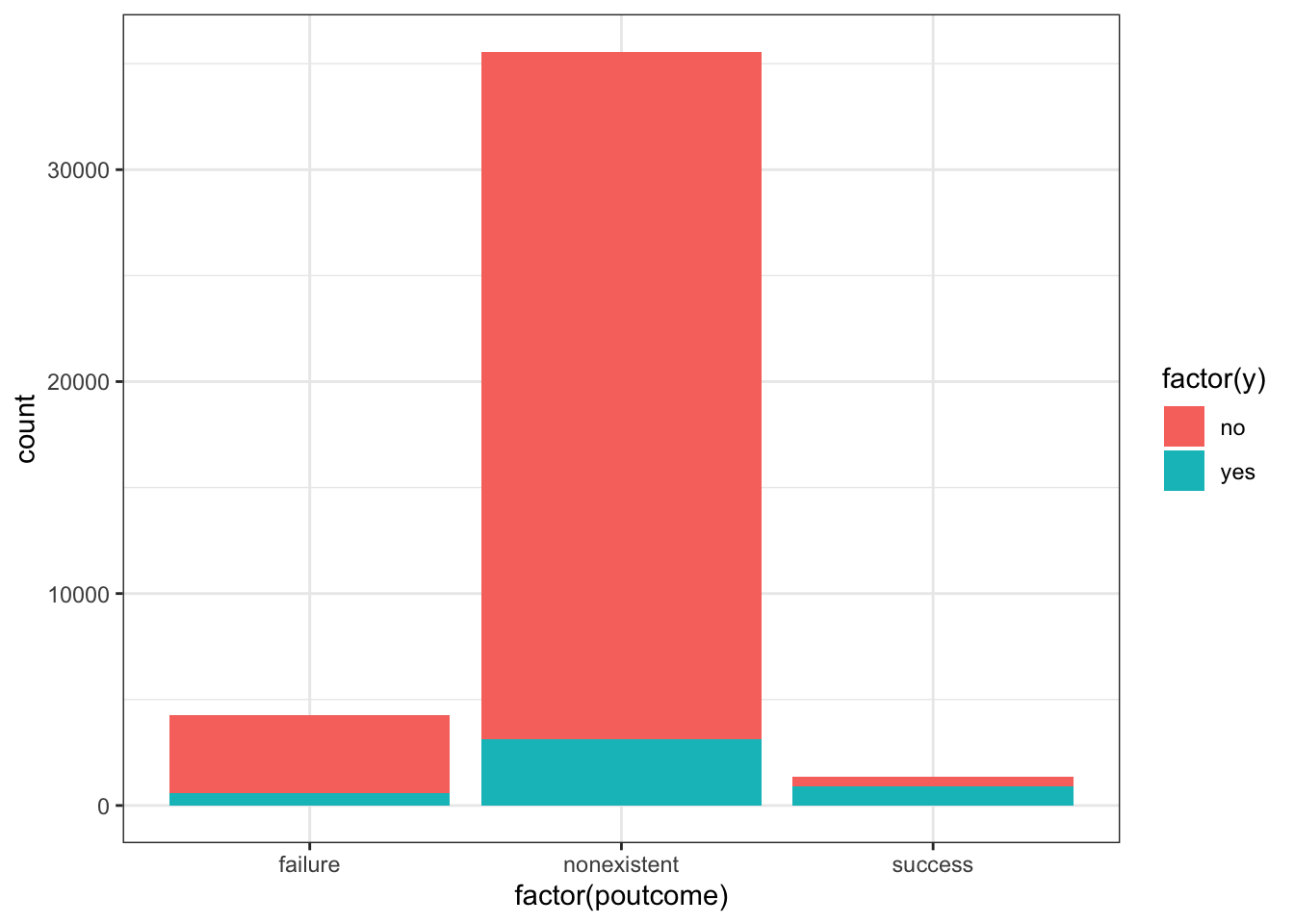
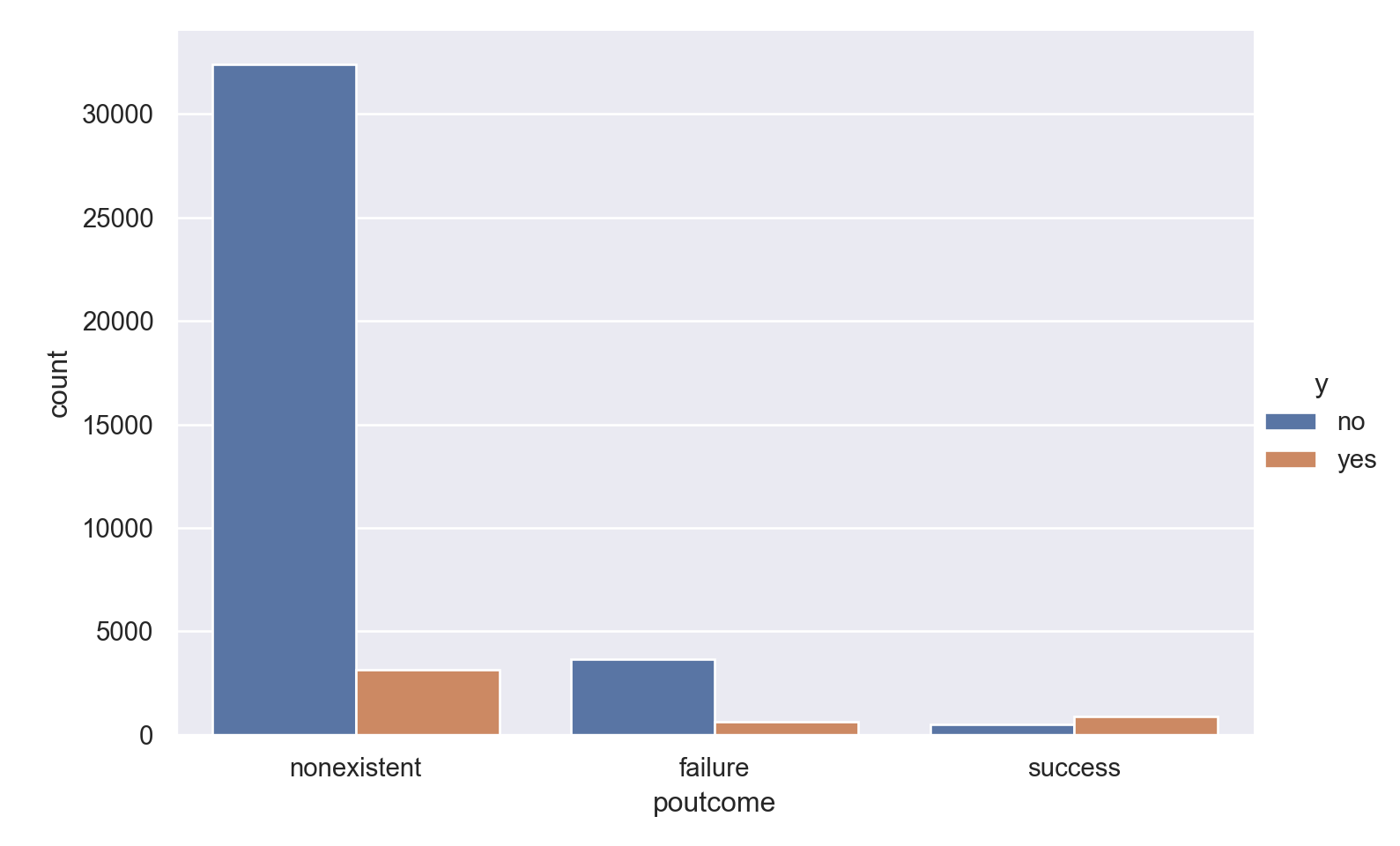
Observations
People with successful outcome in the previous campaign are much more like to have the same outcome in the current campaign.
Most people were not contacted in previous campaigns.
set.seed(1001)
data_bank_marketing=data_bank_marketing %>% mutate(cons.conf.idx = cons.conf.idx + 509) %>% mutate(emp.var.rate = emp.var.rate + 34) %>% mutate(previous = previous + 1) %>% mutate(euribor3m = as.numeric(euribor3m))
data_bank_marketing_split = initial_split(data_bank_marketing, strata = y)
data_bank_marketing_train = training(data_bank_marketing_split)
data_bank_marketing_test = testing(data_bank_marketing_split)
data_folds = vfold_cv(data_bank_marketing_train, strata = y)
# Global modifications applied before train\test split for effective pre-processing
data_bank_marketing["cons.conf.idx"] = data_bank_marketing["cons.conf.idx"] + 509
data_bank_marketing["emp.var.rate"] = data_bank_marketing["emp.var.rate"] + 34
data_bank_marketing["previous"] = data_bank_marketing["previous"] + 1
y = data_bank_marketing["y"]
data_bank_marketing.drop('y', axis=1, inplace=True)
data_bank_marketing.drop('duration', axis=1, inplace=True)
data_bank_marketing_train, data_bank_marketing_test, y_train, y_test = train_test_split(data_bank_marketing, y, random_state=0)
numerical_cols = data_bank_marketing_train.select_dtypes(include=['int64', 'float64']).columns
categorical_cols = data_bank_marketing_train.select_dtypes(include=['object', 'bool']).columns
log_tranform_cols = ['age', 'campaign', 'previous']
cols_index = [data_bank_marketing_train.columns.get_loc(col) for col in log_tranform_cols]
#power_transform_cols = ['cons.conf.idx', 'cons.price.idx', 'nr.employed', 'emp.var.rate', 'euribor3m']
#power_cols_index = [data_bank_marketing_train.columns.get_loc(col) for col in power_transform_cols]
#dummy_cols = ['age', 'duration', 'campaign', 'pdays', 'previous', 'emp.var.rate', 'cons.price.idx', 'cons.conf.idx', 'euribor3m', 'nr.employed']
interact_cols = ['age', 'job']
interact_cols_index = [data_bank_marketing_train.columns.get_loc(col) for col in interact_cols]
# set up the log transformer
log_transform = ColumnTransformer(
transformers=[
('log', FunctionTransformer(np.log1p), cols_index),
],
verbose_feature_names_out=False, # if True, "log_" will be prefixed to the column names that have been transformed
remainder='passthrough' # this allows columns not being transformed to pass through unchanged
)
# this ensures that the transform outputs a DataFrame, so that the column names are available for the next step.
log_transform.set_output(transform='pandas')
# power = ColumnTransformer(
# transformers=[
# ('power', FunctionTransformer(np.square), power_cols_index),
# ],
# verbose_feature_names_out=False,
# remainder='passthrough'
# )
# power.set_output(transform='pandas')ColumnTransformer(remainder='passthrough',
transformers=[('log',
FunctionTransformer(func=<ufunc 'log1p'>),
[0, 10, 12])],
verbose_feature_names_out=False)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
ColumnTransformer(remainder='passthrough',
transformers=[('log',
FunctionTransformer(func=<ufunc 'log1p'>),
[0, 10, 12])],
verbose_feature_names_out=False)[0, 10, 12]
FunctionTransformer(func=<ufunc 'log1p'>)
passthrough
dummy = ColumnTransformer(
transformers=[
('dummy', OneHotEncoder(drop='first', sparse=False), categorical_cols),
],
verbose_feature_names_out=False,
remainder='passthrough'
)
dummy.set_output(transform='pandas')
# interact = ColumnTransformer(
# transformers=[
# ('interact', PolynomialFeatures(interaction_only=True), interact_cols_index),
# ],
# verbose_feature_names_out=False,
# remainder='passthrough'
# )
#
# interact.set_output(transform='pandas')ColumnTransformer(remainder='passthrough',
transformers=[('dummy',
OneHotEncoder(drop='first', sparse=False),
Index(['job', 'marital', 'education', 'default', 'housing', 'loan', 'contact', 'month', 'day_of_week', 'poutcome'], dtype='object'))],
verbose_feature_names_out=False)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
ColumnTransformer(remainder='passthrough',
transformers=[('dummy',
OneHotEncoder(drop='first', sparse=False),
Index(['job', 'marital', 'education', 'default', 'housing', 'loan', 'contact', 'month', 'day_of_week', 'poutcome'], dtype='object'))],
verbose_feature_names_out=False)Index(['job', 'marital', 'education', 'default', 'housing', 'loan', 'contact', 'month', 'day_of_week', 'poutcome'], dtype='object')
OneHotEncoder(drop='first', sparse=False)
passthrough
steps=[
("dummy", dummy),
("normalize", MinMaxScaler()),
("zv", VarianceThreshold()),
]
pipe = Pipeline(steps)
X_trans_train = pipe.fit_transform(data_bank_marketing_train, y_train)
X_trans_test = pipe.fit_transform(data_bank_marketing_test, y_test)
# transform y
label_encoder = LabelEncoder()
y_trans_train = label_encoder.fit_transform(y_train)
y_trans_test = label_encoder.fit_transform(y_test)coerce!(data, Textual => Multiclass);
coerce!(data, :y => OrderedFactor);
schema(data) |> DataFrames.DataFrame |> pretty_table┌────────────────┬──────────────────┬────────────────────────────────────┐
│ names │ scitypes │ types │
│ Symbol │ DataType │ DataType │
├────────────────┼──────────────────┼────────────────────────────────────┤
│ age │ Count │ Int64 │
│ job │ Multiclass{12} │ CategoricalValue{String15, UInt32} │
│ marital │ Multiclass{4} │ CategoricalValue{String15, UInt32} │
│ education │ Multiclass{8} │ CategoricalValue{String31, UInt32} │
│ default │ Multiclass{3} │ CategoricalValue{String7, UInt32} │
│ housing │ Multiclass{3} │ CategoricalValue{String7, UInt32} │
│ loan │ Multiclass{3} │ CategoricalValue{String7, UInt32} │
│ contact │ Multiclass{2} │ CategoricalValue{String15, UInt32} │
│ month │ Multiclass{10} │ CategoricalValue{String3, UInt32} │
│ day_of_week │ Multiclass{5} │ CategoricalValue{String3, UInt32} │
│ duration │ Count │ Int64 │
│ campaign │ Count │ Int64 │
│ pdays │ Count │ Int64 │
│ previous │ Count │ Int64 │
│ poutcome │ Multiclass{3} │ CategoricalValue{String15, UInt32} │
│ emp.var.rate │ Continuous │ Float64 │
│ cons.price.idx │ Continuous │ Float64 │
│ cons.conf.idx │ Continuous │ Float64 │
│ euribor3m │ Continuous │ Float64 │
│ nr_employed │ Continuous │ Float64 │
│ y │ OrderedFactor{2} │ CategoricalValue{String3, UInt32} │
└────────────────┴──────────────────┴────────────────────────────────────┘- Log and square transforms applied to numeric predictors.
- Dummy transform needed for categorical predictors.
- Interactions defined for age with job and education.
base_rec = recipe(y ~ ., data = data_bank_marketing_train) %>% step_rm(duration) #%>% step_zv(all_numeric_predictors()) %>% step_normalize(all_numeric_predictors()) %>% step_pca(all_numeric_predictors())
trfm_rec = base_rec %>% step_log(c(age, campaign, previous)) %>% step_poly(c(pdays, cons.conf.idx, cons.price.idx, nr.employed, emp.var.rate, euribor3m)) %>% step_dummy(all_nominal_predictors()) %>% step_interact(terms =~ age:starts_with("job") + age:starts_with("education"))
trfm_data = prep(trfm_rec, data_bank_marketing_train) %>% bake(new_data = NULL)
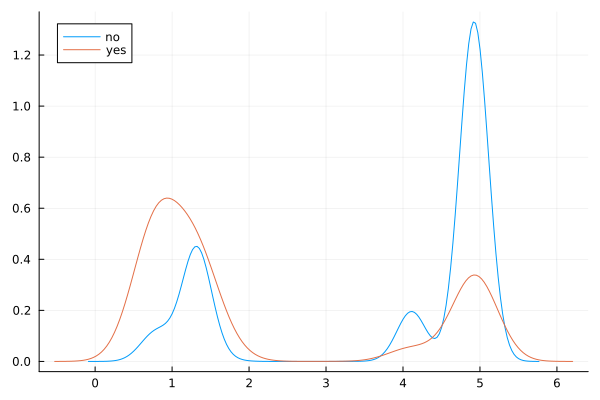
p1 = ggplot(trfm_data) + geom_density(aes(x=(campaign), color=factor(y)))
p2 = ggplot(trfm_data) + geom_density(aes(x=(age), color=factor(y)))
p3 = ggplot(trfm_data) + geom_density(aes(x=(previous), color=factor(y)))
p4 = ggplot(trfm_data) + geom_density(aes(x=(cons.conf.idx_poly_2), color=factor(y)))
p5 = ggplot(trfm_data) + geom_density(aes(x=(pdays_poly_2), color=factor(y)))
p6 = ggplot(trfm_data) + geom_density(aes(x=(cons.price.idx_poly_2), color=factor(y)))
p7 = ggplot(trfm_data) + geom_density(aes(x=(euribor3m_poly_2), color=factor(y)))
p8 = ggplot(trfm_data) + geom_density(aes(x=(nr.employed_poly_2), color=factor(y)))
p9 = ggplot(trfm_data) + geom_density(aes(x=(emp.var.rate_poly_2), color=factor(y)))
p1+p2+p3+p4 + plot_layout(ncol = 2)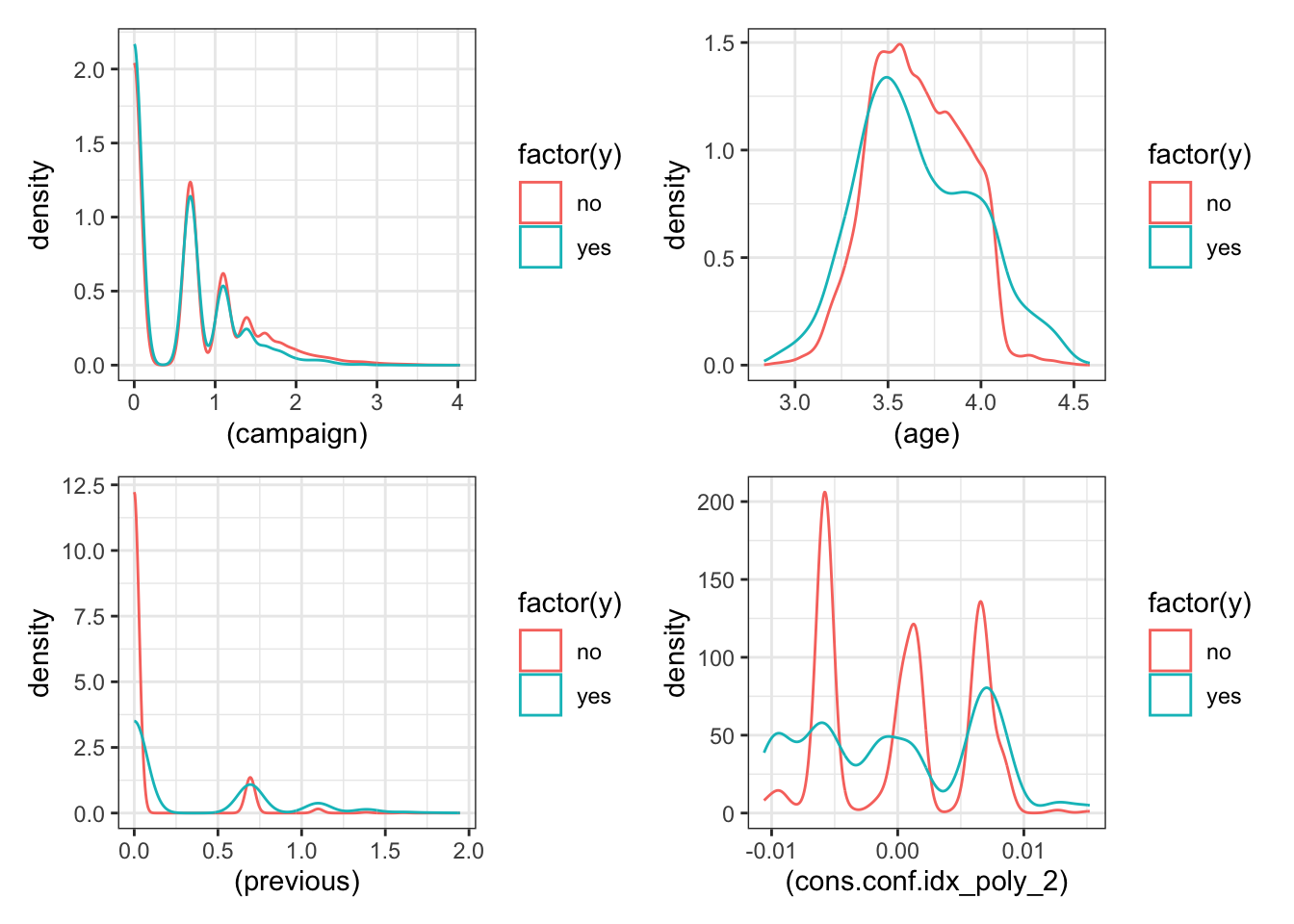
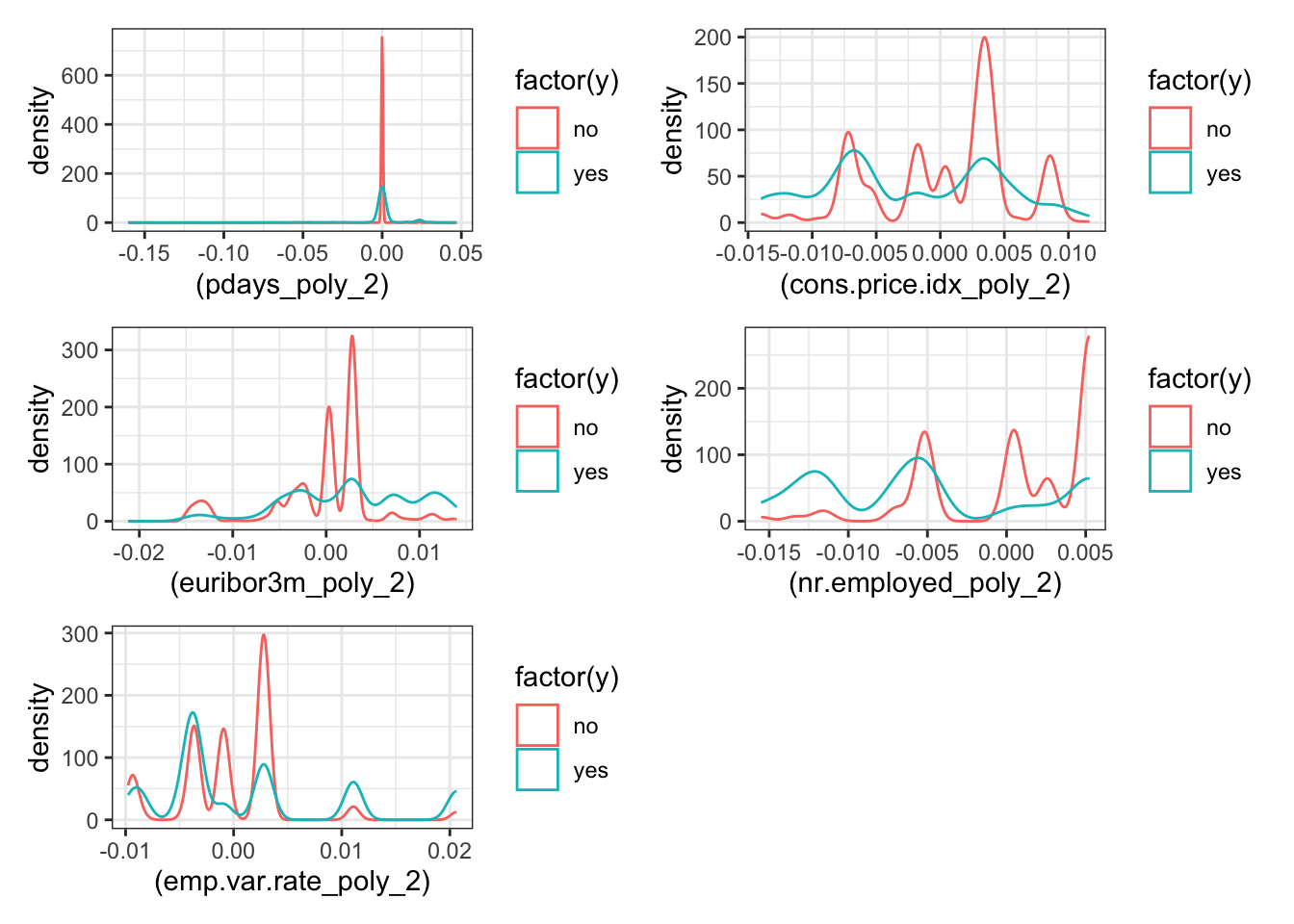
numerical_cols = data_bank_marketing_train.select_dtypes(include=['int64', 'float64']).columns
categorical_cols = data_bank_marketing_train.select_dtypes(include=['object', 'bool']).columns
log_tranform_cols = ['age', 'campaign', 'previous']
cols_index = [data_bank_marketing_train.columns.get_loc(col) for col in log_tranform_cols]
#power_transform_cols = ['cons.conf.idx', 'cons.price.idx', 'nr.employed', 'emp.var.rate', 'euribor3m']
#power_cols_index = [data_bank_marketing_train.columns.get_loc(col) for col in power_transform_cols]
#dummy_cols = ['age', 'duration', 'campaign', 'pdays', 'previous', 'emp.var.rate', 'cons.price.idx', 'cons.conf.idx', 'euribor3m', 'nr.employed']
interact_cols = ['age', 'job']
interact_cols_index = [data_bank_marketing_train.columns.get_loc(col) for col in interact_cols]
# set up the log transformer
log_transform = ColumnTransformer(
transformers=[
('log', FunctionTransformer(np.log1p), cols_index),
],
verbose_feature_names_out=False, # if True, "log_" will be prefixed to the column names that have been transformed
remainder='passthrough' # this allows columns not being transformed to pass through unchanged
)
# this ensures that the transform outputs a DataFrame, so that the column names are available for the next step.
log_transform.set_output(transform='pandas')
# power = ColumnTransformer(
# transformers=[
# ('power', FunctionTransformer(np.square), power_cols_index),
# ],
# verbose_feature_names_out=False,
# remainder='passthrough'
# )
# power.set_output(transform='pandas')ColumnTransformer(remainder='passthrough',
transformers=[('log',
FunctionTransformer(func=<ufunc 'log1p'>),
[0, 10, 12])],
verbose_feature_names_out=False)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
ColumnTransformer(remainder='passthrough',
transformers=[('log',
FunctionTransformer(func=<ufunc 'log1p'>),
[0, 10, 12])],
verbose_feature_names_out=False)[0, 10, 12]
FunctionTransformer(func=<ufunc 'log1p'>)
passthrough
dummy = ColumnTransformer(
transformers=[
('dummy', OneHotEncoder(drop='first', sparse=False), categorical_cols),
],
verbose_feature_names_out=False,
remainder='passthrough'
)
dummy.set_output(transform='pandas')
# interact = ColumnTransformer(
# transformers=[
# ('interact', PolynomialFeatures(interaction_only=True), interact_cols_index),
# ],
# verbose_feature_names_out=False,
# remainder='passthrough'
# )
#
# interact.set_output(transform='pandas')ColumnTransformer(remainder='passthrough',
transformers=[('dummy',
OneHotEncoder(drop='first', sparse=False),
Index(['job', 'marital', 'education', 'default', 'housing', 'loan', 'contact', 'month', 'day_of_week', 'poutcome'], dtype='object'))],
verbose_feature_names_out=False)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
ColumnTransformer(remainder='passthrough',
transformers=[('dummy',
OneHotEncoder(drop='first', sparse=False),
Index(['job', 'marital', 'education', 'default', 'housing', 'loan', 'contact', 'month', 'day_of_week', 'poutcome'], dtype='object'))],
verbose_feature_names_out=False)Index(['job', 'marital', 'education', 'default', 'housing', 'loan', 'contact', 'month', 'day_of_week', 'poutcome'], dtype='object')
OneHotEncoder(drop='first', sparse=False)
passthrough
Observations
- Some of the predictors have a reduction in the skew after the transformation.
glmnet_recipe <-
recipe(formula = y ~ ., data = data_bank_marketing_train) %>%
step_rm(duration) %>%
step_log(c(age, campaign, previous)) %>%
#step_poly(c(pdays, cons.conf.idx, cons.price.idx, nr.employed, emp.var.rate, euribor3m)) %>%
## For modeling, it is preferred to encode qualitative data as factors
## (instead of character).
step_string2factor(one_of("job", "marital", "education", "default", "housing",
"loan", "contact", "month", "day_of_week", "poutcome", "y")) %>%
step_novel(all_nominal_predictors()) %>%
## This model requires the predictors to be numeric. The most common
## method to convert qualitative predictors to numeric is to create
## binary indicator variables (aka dummy variables) from these
## predictors.
step_dummy(all_nominal_predictors()) %>%
## Regularization methods sum up functions of the model slope
## coefficients. Because of this, the predictor variables should be on
## the same scale. Before centering and scaling the numeric predictors,
## any predictors with a single unique value are filtered out.
step_zv(all_predictors()) %>%
step_normalize(all_numeric_predictors())
glmnet_spec <-
multinom_reg(penalty = tune(), mixture = tune()) %>%
set_mode("classification") %>%
set_engine("glmnet")
glmnet_workflow <-
workflow() %>%
add_recipe(glmnet_recipe) %>%
add_model(glmnet_spec)
glmnet_grid <- tidyr::crossing(penalty = 10^seq(-6, -1, length.out = 20), mixture = c(0.05,
0.2, 0.4, 0.6, 0.8, 1))
# glmnet_tune <-
# tune_grid(glmnet_workflow, resamples = data_folds, grid = glmnet_grid, control = control_grid(save_pred = TRUE), metrics = metric_set(roc_auc))
final_params <-
tibble(
penalty = 0.0000695,
mixture = 1
)
final_glmnet_wflow = glmnet_workflow %>% finalize_workflow(final_params)
final_glmnet_wflow══ Workflow ════════════════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: multinom_reg()
── Preprocessor ────────────────────────────────────────────────────────────────
7 Recipe Steps
• step_rm()
• step_log()
• step_string2factor()
• step_novel()
• step_dummy()
• step_zv()
• step_normalize()
── Model ───────────────────────────────────────────────────────────────────────
Multinomial Regression Model Specification (classification)
Main Arguments:
penalty = 6.95e-05
mixture = 1
Computational engine: glmnet final_glmnet_fit = final_glmnet_wflow %>% last_fit(data_bank_marketing_split)
final_glmnet_fit %>% collect_metrics()# A tibble: 2 × 4
.metric .estimator .estimate .config
<chr> <chr> <dbl> <chr>
1 accuracy binary 0.901 Preprocessor1_Model1
2 roc_auc binary 0.793 Preprocessor1_Model1# A tibble: 10,297 × 7
id .pred_no .pred_yes .row .pred_class y .config
<chr> <dbl> <dbl> <int> <fct> <fct> <chr>
1 train/test split 0.970 0.0299 7 no no Preprocessor1_Mo…
2 train/test split 0.977 0.0225 18 no no Preprocessor1_Mo…
3 train/test split 0.968 0.0321 21 no no Preprocessor1_Mo…
4 train/test split 0.980 0.0201 22 no no Preprocessor1_Mo…
5 train/test split 0.970 0.0296 24 no no Preprocessor1_Mo…
6 train/test split 0.985 0.0155 30 no no Preprocessor1_Mo…
7 train/test split 0.977 0.0230 34 no no Preprocessor1_Mo…
8 train/test split 0.975 0.0255 35 no no Preprocessor1_Mo…
9 train/test split 0.969 0.0313 43 no no Preprocessor1_Mo…
10 train/test split 0.973 0.0265 52 no no Preprocessor1_Mo…
# … with 10,287 more rows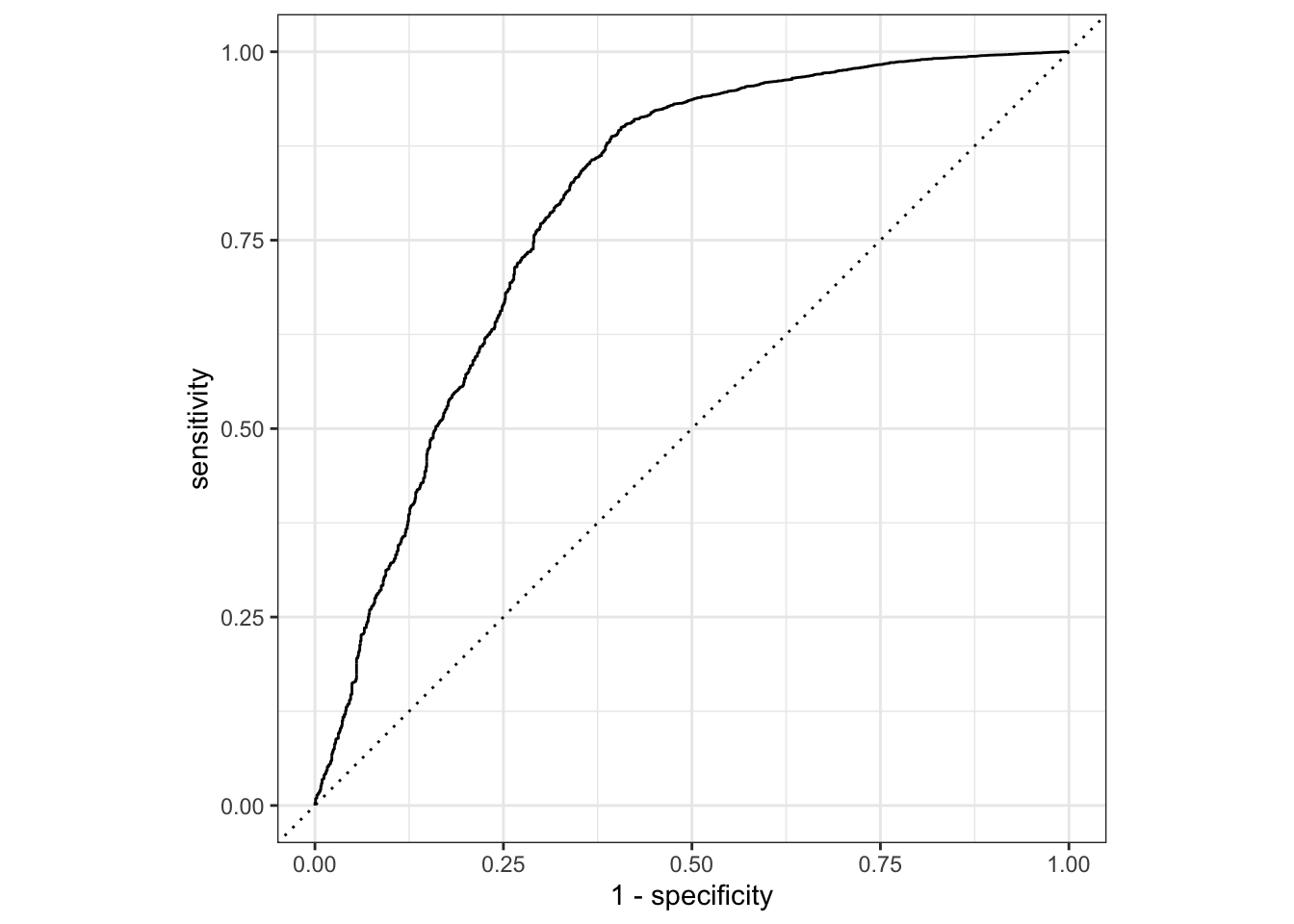
def roc_plot(X_test,Y_test, fitted_model, pos_label='yes'):
# calculate the fpr and tpr for all thresholds of the classification
probs = fitted_model.predict_proba(X_test)
probs_no = probs[:,1]
fpr, tpr, threshold = metrics.roc_curve(Y_test, probs_no, pos_label = pos_label)
roc_auc = metrics.auc(fpr, tpr)
plt.clf()
plt.title('Receiver Operating Characteristic')
plt.plot(fpr, tpr, 'b', label = 'AUC = %0.2f' % roc_auc)
plt.legend(loc = 'lower right')
plt.plot([0, 1], [0, 1],'r--')
plt.xlim([0, 1])
plt.ylim([0, 1])
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')
plt.show()
return roc_auc
def grid_search_fit(pipe, param_grid, X_train, Y_train, X_test, Y_test, cv=10, scoring='roc_auc', plot=True, report=False):
grid = GridSearchCV(pipe, param_grid, cv=10, scoring=scoring)
grid.fit(X_train, Y_train)
fitted_model=grid.best_estimator_
score=grid.score(X_test, Y_test)
yhat=grid.predict(X_test)
if report:
print(metrics.classification_report(Y_test, yhat))
if plot:
roc_plot(X_test, Y_test, fitted_model, 'yes')
return (fitted_model, score, yhat)
model = LogisticRegression(penalty='elasticnet', solver='saga', max_iter=1000)
#model = SGDClassifier(max_iter=1000, penalty='elasticnet')
steps.append(("model", model))
param_grid = {'model__l1_ratio':np.arange(0,1,0.1)}
# param_grid = [
# {'penalty' : ['l1', 'l2', 'elasticnet', 'none'],
# 'C' : np.logspace(-4, 4, 20),
# 'solver' : ['lbfgs','newton-cg','liblinear','sag','saga'],
# 'max_iter' : [100, 1000,2500, 5000]
# }
# ]
pipe = Pipeline(steps)
grid = GridSearchCV(pipe, param_grid, cv=10, scoring='roc_auc')
grid.fit(data_bank_marketing_train, y_train)GridSearchCV(cv=10,
estimator=Pipeline(steps=[('dummy',
ColumnTransformer(remainder='passthrough',
transformers=[('dummy',
OneHotEncoder(drop='first',
sparse=False),
Index(['job', 'marital', 'education', 'default', 'housing', 'loan', 'contact', 'month', 'day_of_week', 'poutcome'], dtype='object'))],
verbose_feature_names_out=False)),
('normalize', MinMaxScaler()),
('zv', VarianceThreshold()),
('model',
LogisticRegression(max_iter=1000,
penalty='elasticnet',
solver='saga'))]),
param_grid={'model__l1_ratio': array([0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9])},
scoring='roc_auc')In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
GridSearchCV(cv=10,
estimator=Pipeline(steps=[('dummy',
ColumnTransformer(remainder='passthrough',
transformers=[('dummy',
OneHotEncoder(drop='first',
sparse=False),
Index(['job', 'marital', 'education', 'default', 'housing', 'loan', 'contact', 'month', 'day_of_week', 'poutcome'], dtype='object'))],
verbose_feature_names_out=False)),
('normalize', MinMaxScaler()),
('zv', VarianceThreshold()),
('model',
LogisticRegression(max_iter=1000,
penalty='elasticnet',
solver='saga'))]),
param_grid={'model__l1_ratio': array([0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9])},
scoring='roc_auc')Pipeline(steps=[('dummy',
ColumnTransformer(remainder='passthrough',
transformers=[('dummy',
OneHotEncoder(drop='first',
sparse=False),
Index(['job', 'marital', 'education', 'default', 'housing', 'loan', 'contact', 'month', 'day_of_week', 'poutcome'], dtype='object'))],
verbose_feature_names_out=False)),
('normalize', MinMaxScaler()), ('zv', VarianceThreshold()),
('model',
LogisticRegression(max_iter=1000, penalty='elasticnet',
solver='saga'))])ColumnTransformer(remainder='passthrough',
transformers=[('dummy',
OneHotEncoder(drop='first', sparse=False),
Index(['job', 'marital', 'education', 'default', 'housing', 'loan', 'contact', 'month', 'day_of_week', 'poutcome'], dtype='object'))],
verbose_feature_names_out=False)Index(['job', 'marital', 'education', 'default', 'housing', 'loan', 'contact', 'month', 'day_of_week', 'poutcome'], dtype='object')
OneHotEncoder(drop='first', sparse=False)
['age', 'campaign', 'pdays', 'previous', 'emp.var.rate', 'cons.price.idx', 'cons.conf.idx', 'euribor3m', 'nr.employed']
passthrough
MinMaxScaler()
VarianceThreshold()
LogisticRegression(max_iter=1000, penalty='elasticnet', solver='saga')
{'model__l1_ratio': 0.6000000000000001}fitted_model=grid.best_estimator_
score=grid.score(data_bank_marketing_test, y_test)
#score
yhat=grid.predict_proba(data_bank_marketing_test)
roc_plot(data_bank_marketing_test, y_test, fitted_model, 'yes')
#sgdclass_param_grid = {'model__alpha': [0.0001, 0.001, 0.01, 0.1, 1, 10, 100],
# "model__l1_ratio": np.arange(0.0, 1.0, 0.1)}0.7904608842023623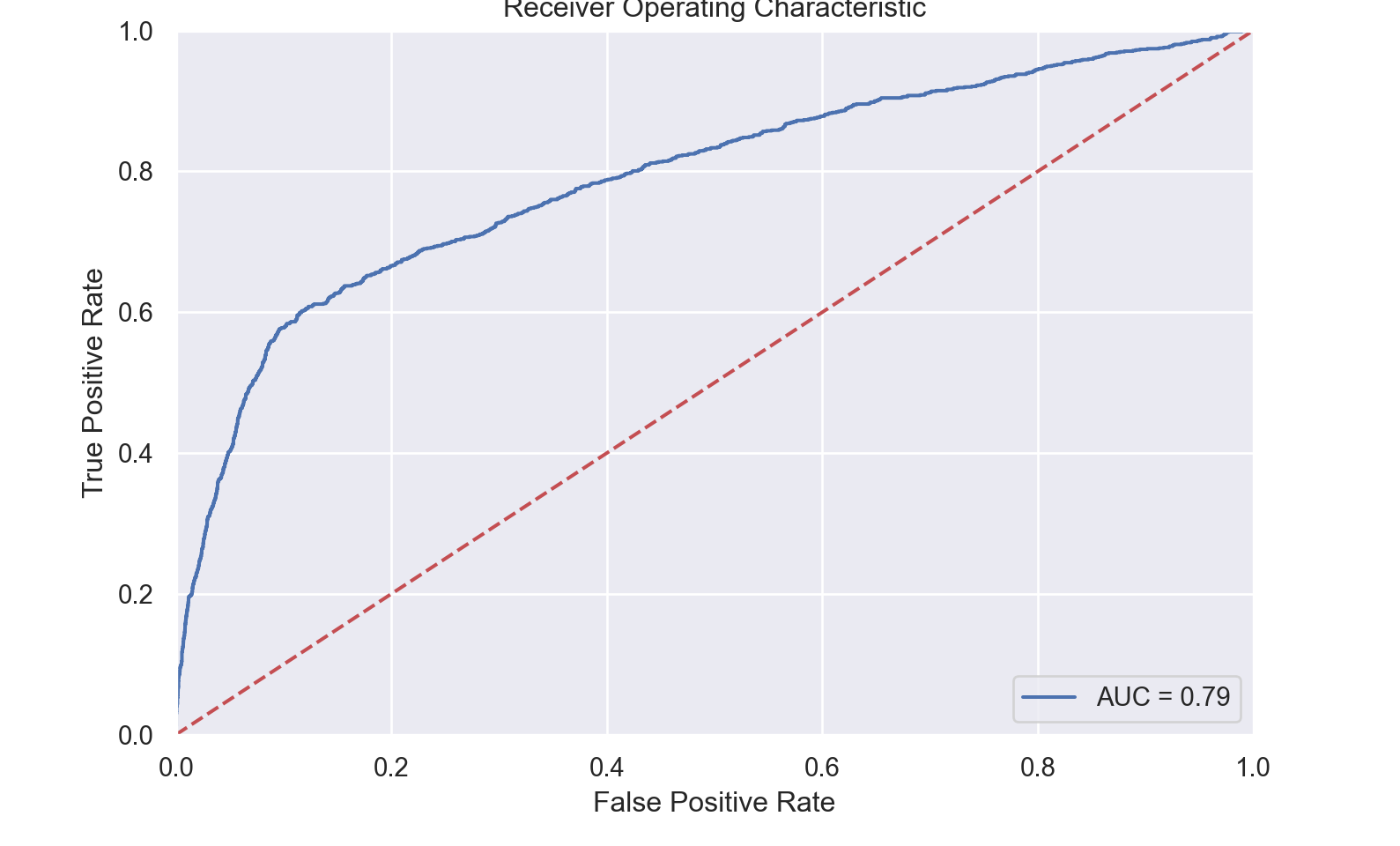
import MLJLinearModels.LogisticClassifier
LinearBinaryClassifier = MLJLinearModels.LogisticClassifierLogisticClassifierProbabilisticPipeline(
standardizer = Standardizer(
features = Symbol[],
ignore = false,
ordered_factor = false,
count = false),
continuous_encoder = ContinuousEncoder(
drop_last = false,
one_hot_ordered_factors = false),
logistic_classifier = LogisticClassifier(
lambda = 2.220446049250313e-16,
gamma = 0.0,
penalty = :l2,
fit_intercept = true,
penalize_intercept = false,
scale_penalty_with_samples = true,
solver = nothing),
cache = true)
#tuning = RandomSearch(rng=123);
tuning = Grid(rng=123);
# tuning=LatinHypercube(gens = 1,
# popsize = 100,
# ntour = 2,
# ptour = 0.8,
# interSampleWeight = 1.0,
# ae_power = 2,
# periodic_ae = false,
# rng=123)
r = range(model,
:(logistic_classifier.lambda),
lower=0,
upper=1,
unit=0.01)NumericRange(0 ≤ logistic_classifier.lambda ≤ 1; origin=0.5, unit=0.01)NumericRange(0 ≤ logistic_classifier.gamma ≤ 1; origin=0.5, unit=0.01)
tuned_model = TunedModel(model=model,
ranges=[r, s],
resampling=CV(nfolds=10),
measures=auc,
tuning=tuning,
n=200);
tuned_mach = machine(tuned_model, X_train, y_train);
fit!(tuned_mach);
yhat=MLJ.predict(tuned_mach, X_test);
rep = report(tuned_mach);
print(
"Measurements:\n",
" brier loss: ", brier_loss(yhat,y_test) |> mean, "\n",
" auc: ", auc(yhat,y_test), "\n",
" accuracy: ", accuracy(mode.(yhat), y_test)
)Measurements:
brier loss: 0.16162546559785088
auc: 0.769700437197346
accuracy: 0.9018290708967304
# LogisticModel = machine(LinearBinaryClassifierPipe, X_train, y_train);
# fit!(LogisticModel);
# fp = fitted_params(LogisticModel);
# fp.logistic_classifier
#keys(fp)
#rpt = report(LogisticModel)
#keys(rpt)
# fi = rpt.linear_binary_classifier.coef_table |> DataFrames.DataFrame
#ŷ = MLJ.predict(LogisticModel, X_test);
#
# print(
# "Measurements:\n",
# " brier loss: ", brier_loss(ŷ,y_test) |> mean, "\n",
# " auc: ", auc(ŷ,y_test), "\n",
# " accuracy: ", accuracy(mode.(ŷ), y_test)
# )
#
# #confmat(mode.(ŷ),y_test)
#
# e_pipe = evaluate(LinearBinaryClassifierPipe, X_train, y_train,
# resampling=StratifiedCV(nfolds=6, rng=42),
# measures=[brier_loss, auc, accuracy],
# repeats=1,
# acceleration=CPUThreads())
#show(iterated_pipe, 2)
# iterated_pipe = IteratedModel(model=LinearBinaryClassifierPipe,
# controls=controls,
# measure=auc,
# resampling=StratifiedCV(nfolds=6, rng=42))
#mach_iterated_pipe = machine(LinearBinaryClassifierPipe, X_train, y_train);
#fit!(mach_iterated_pipe);
#residuals = [1 - pdf(ŷ[i], y_test[i,1]) for i in 1:nrow(y_test)]
# r = report(LogisticModel)
#
# k = collect(keys(fp.fitted_params_given_machine))[3]
# println("\n Coefficients: ", fp.fitted_params_given_machine[k].coef)
# println("\n y \n ", y_test[1:5,1])
# println("\n ŷ \n ", ŷ[1:5])
# println("\n residuals \n ", residuals[1:5])
# println("\n Standard Error per Coefficient \n", r.linear_binary_classifier.stderror[2:end])
#confusion_matrix(yMode, y_test)nb_recipe <-
recipe(formula = y ~ ., data = data_bank_marketing_train) %>%
step_rm(duration) %>%
step_dummy()
nb_spec <-
naive_Bayes(smoothness = tune(), Laplace = tune()) %>%
set_engine("naivebayes")
nb_workflow <-
workflow() %>%
add_recipe(nb_recipe) %>%
add_model(nb_spec)
#nb_params = extract_parameter_set_dials(nb_spec)
# nb_grid = nb_params %>% grid_latin_hypercube(size = 20, original = FALSE)
#
# nb_tune <-
# nb_workflow %>%
# tune_grid(
# data_folds,
# grid = nb_grid
# )
# nb_tune
# select_best(nb_tune, metric = "roc_auc")
final_params = tibble(
smoothness = 0.5923033,
Laplace = 0.4830422
)
final_nb_wflow <-
nb_workflow %>%
finalize_workflow(final_params)
final_nb_fit <-
final_nb_wflow %>%
last_fit(data_bank_marketing_split)
final_nb_fit %>% collect_metrics()# A tibble: 2 × 4
.metric .estimator .estimate .config
<chr> <chr> <dbl> <chr>
1 accuracy binary 0.880 Preprocessor1_Model1
2 roc_auc binary 0.795 Preprocessor1_Model1# A tibble: 10,297 × 7
id .pred_no .pred_yes .row .pred_class y .config
<chr> <dbl> <dbl> <int> <fct> <fct> <chr>
1 train/test split 1.00 0.00000488 7 no no Preprocessor1_…
2 train/test split 1.00 0.000000414 18 no no Preprocessor1_…
3 train/test split 1.00 0.00000451 21 no no Preprocessor1_…
4 train/test split 1.00 0.000000644 22 no no Preprocessor1_…
5 train/test split 1.00 0.00000345 24 no no Preprocessor1_…
6 train/test split 1.00 0.000000957 30 no no Preprocessor1_…
7 train/test split 1.00 0.00000110 34 no no Preprocessor1_…
8 train/test split 1.00 0.00000159 35 no no Preprocessor1_…
9 train/test split 1.00 0.00000488 43 no no Preprocessor1_…
10 train/test split 1.00 0.00000200 52 no no Preprocessor1_…
# … with 10,287 more rows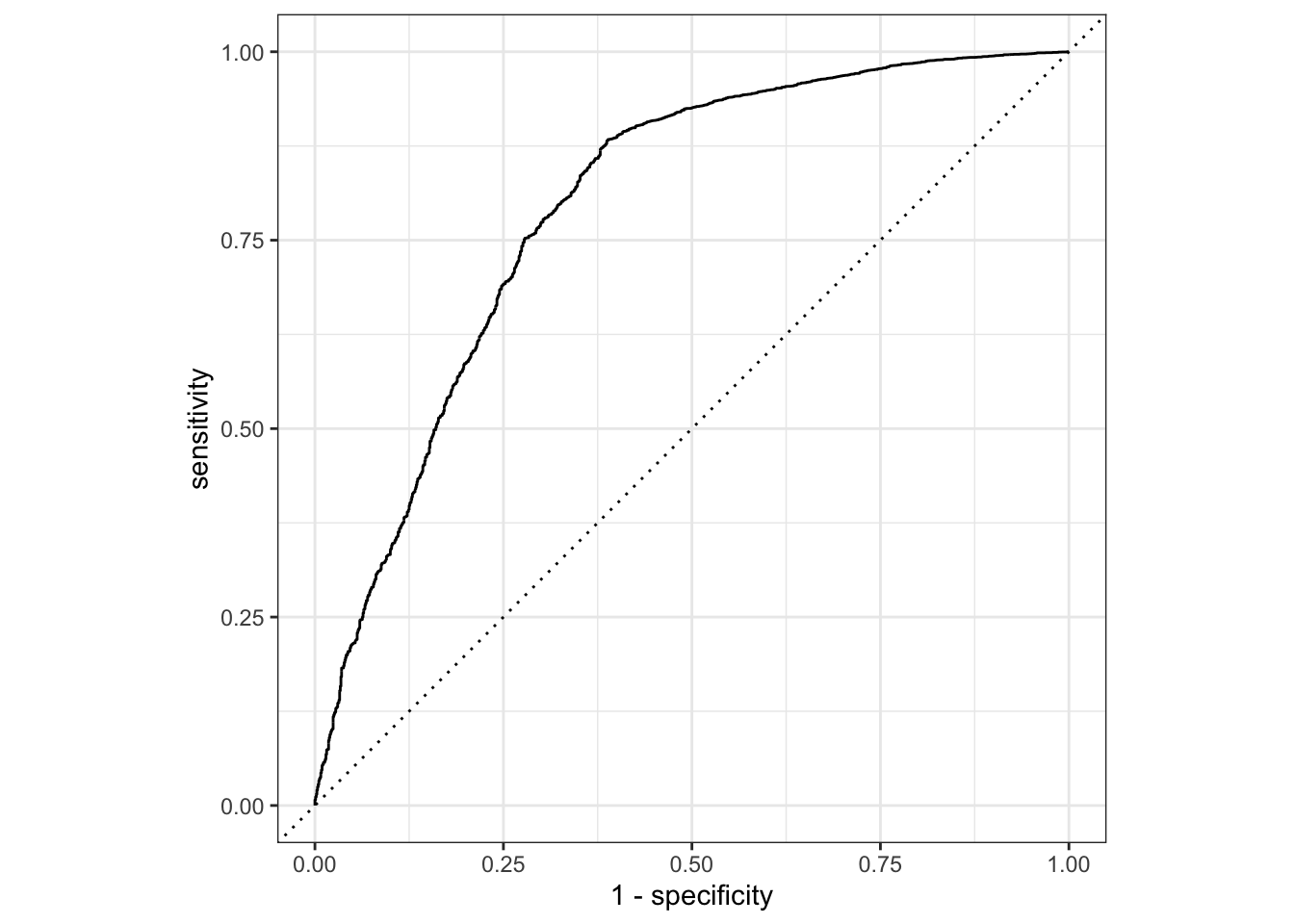
GaussianNB()In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
GaussianNB()
array([[9.99990953e-01, 9.04749432e-06],
[8.12354222e-01, 1.87645778e-01],
[9.99999789e-01, 2.10792883e-07],
...,
[9.99294556e-01, 7.05443805e-04],
[9.99995515e-01, 4.48497521e-06],
[7.16817215e-01, 2.83182785e-01]])0.7567412601500412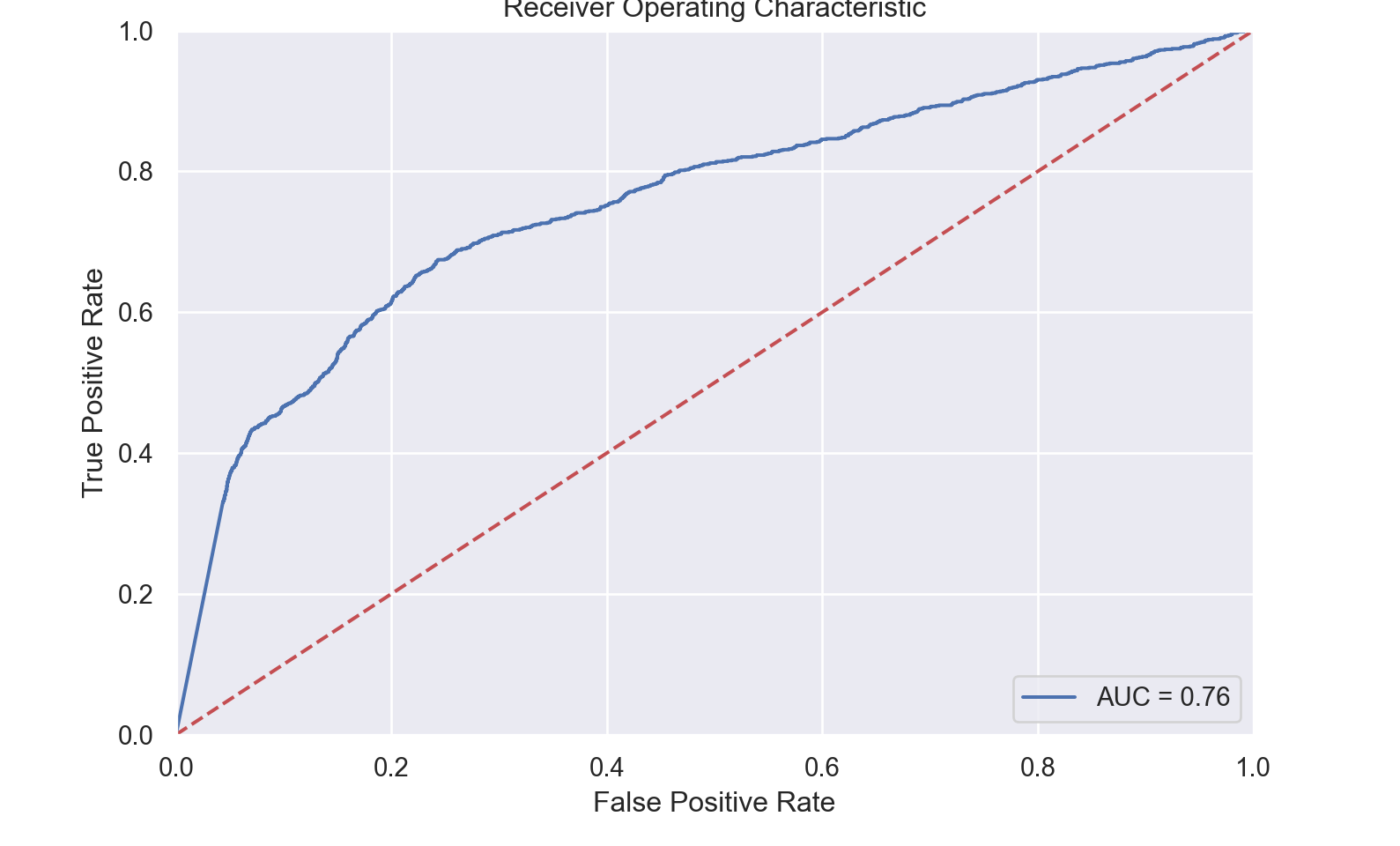
import NaiveBayes
GaussianNBClassifier = @load GaussianNBClassifier pkg=NaiveBayes;
model = Standardizer |> ContinuousEncoder |> GaussianNBClassifier()ProbabilisticPipeline(
standardizer = Standardizer(
features = Symbol[],
ignore = false,
ordered_factor = false,
count = false),
continuous_encoder = ContinuousEncoder(
drop_last = false,
one_hot_ordered_factors = false),
gaussian_nb_classifier = GaussianNBClassifier(),
cache = true)
# Model training fails with error: nested task error: PosDefException: matrix is not positive definite; Cholesky factorization failed.
# Pre-processing to eliminate collinearity may be needed
# mach = machine(model, X_train, y_train);
#
# fit!(mach);
# yhat=MLJ.predict(mach, X_test);
# rep = report(mach);
# print(
# "Measurements:\n",
# " brier loss: ", brier_loss(yhat,y_test) |> mean, "\n",
# " auc: ", auc(yhat,y_test), "\n",
# " accuracy: ", accuracy(mode.(yhat), y_test)
# )#use_kknn(y ~ ., data = data_bank_marketing_train)
kknn_recipe <-
recipe(formula = y ~ ., data = data_bank_marketing_train) %>%
step_rm(duration) %>%
step_string2factor(one_of("job", "marital", "education", "default", "housing",
"loan", "contact", "month", "day_of_week", "poutcome", "y")) %>%
step_novel(all_nominal_predictors()) %>%
step_dummy(all_nominal_predictors()) %>%
step_zv(all_predictors()) %>%
step_normalize(all_numeric_predictors())
kknn_spec <-
nearest_neighbor(neighbors = tune()) %>%
set_mode("classification") %>%
set_engine("kknn")
kknn_param = extract_parameter_set_dials(kknn_spec)
kknn_workflow <-
workflow() %>%
add_recipe(kknn_recipe) %>%
add_model(kknn_spec)
set.seed(66214)
# kknn_tune <-
# tune_grid(kknn_workflow, resamples = data_folds, size =10)
final_params <-
tibble(
neighbors = 14
)
final_kknn_wflow = kknn_workflow %>% finalize_workflow(final_params)
final_kknn_wflow══ Workflow ════════════════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: nearest_neighbor()
── Preprocessor ────────────────────────────────────────────────────────────────
6 Recipe Steps
• step_rm()
• step_string2factor()
• step_novel()
• step_dummy()
• step_zv()
• step_normalize()
── Model ───────────────────────────────────────────────────────────────────────
K-Nearest Neighbor Model Specification (classification)
Main Arguments:
neighbors = 14
Computational engine: kknn final_kknn_fit = final_kknn_wflow %>% last_fit(data_bank_marketing_split)
final_kknn_fit %>% collect_metrics()# A tibble: 2 × 4
.metric .estimator .estimate .config
<chr> <chr> <dbl> <chr>
1 accuracy binary 0.894 Preprocessor1_Model1
2 roc_auc binary 0.751 Preprocessor1_Model1# A tibble: 10,297 × 7
id .pred_no .pred_yes .row .pred_class y .config
<chr> <dbl> <dbl> <int> <fct> <fct> <chr>
1 train/test split 1 0 7 no no Preprocessor1_Mo…
2 train/test split 0.932 0.0682 18 no no Preprocessor1_Mo…
3 train/test split 1 0 21 no no Preprocessor1_Mo…
4 train/test split 0.932 0.0682 22 no no Preprocessor1_Mo…
5 train/test split 1 0 24 no no Preprocessor1_Mo…
6 train/test split 1 0 30 no no Preprocessor1_Mo…
7 train/test split 0.749 0.251 34 no no Preprocessor1_Mo…
8 train/test split 1 0 35 no no Preprocessor1_Mo…
9 train/test split 1 0 43 no no Preprocessor1_Mo…
10 train/test split 1 0 52 no no Preprocessor1_Mo…
# … with 10,287 more rows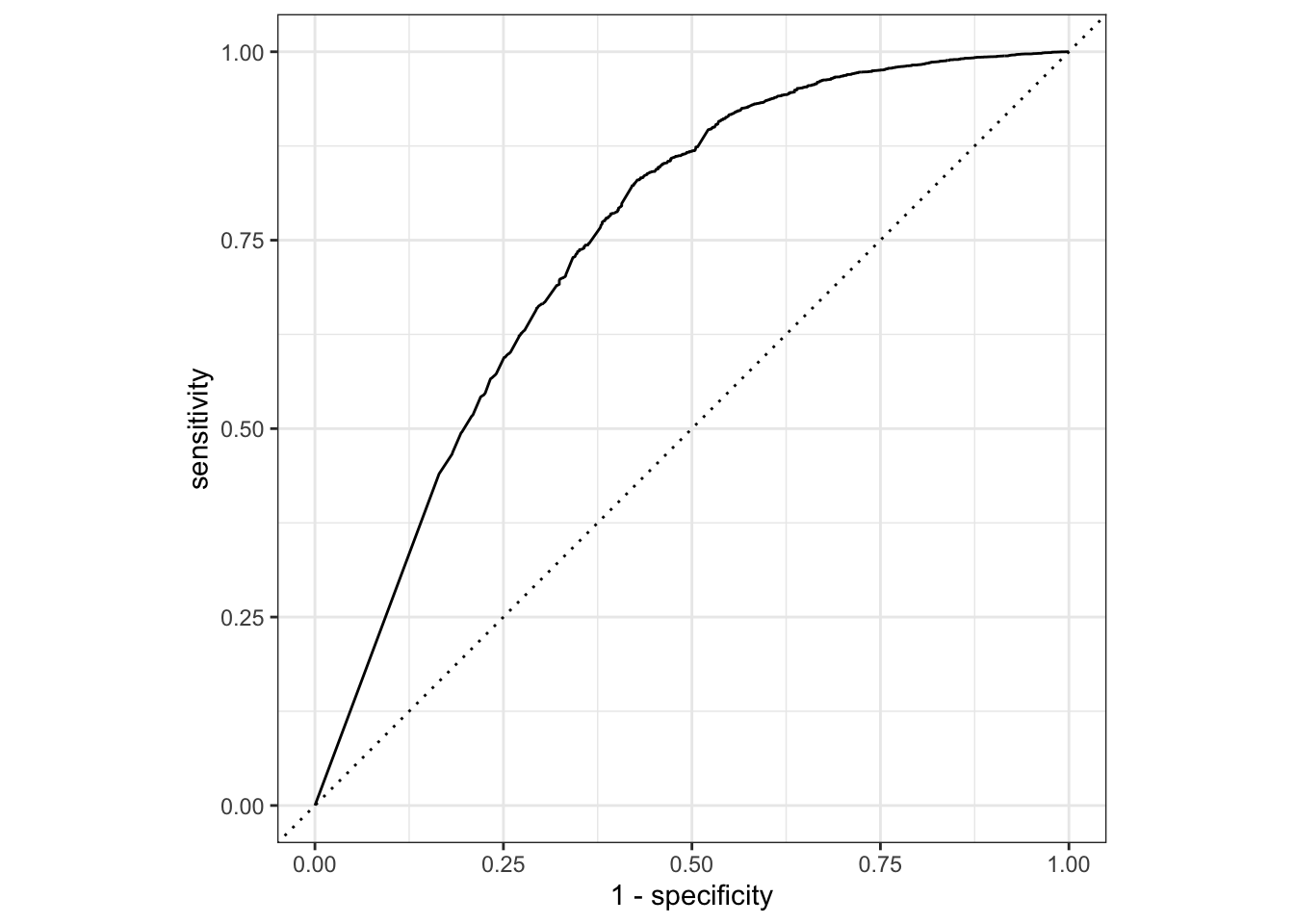
model = KNeighborsClassifier()
param_grid = {'model__n_neighbors':np.arange(0,20,1)}
steps[-1] = ("model", model)
pipe = Pipeline(steps)
grid = GridSearchCV(pipe, param_grid, cv=10, scoring='roc_auc')
grid.fit(data_bank_marketing_train, y_train)GridSearchCV(cv=10,
estimator=Pipeline(steps=[('dummy',
ColumnTransformer(remainder='passthrough',
transformers=[('dummy',
OneHotEncoder(drop='first',
sparse=False),
Index(['job', 'marital', 'education', 'default', 'housing', 'loan', 'contact', 'month', 'day_of_week', 'poutcome'], dtype='object'))],
verbose_feature_names_out=False)),
('normalize', MinMaxScaler()),
('zv', VarianceThreshold()),
('model', KNeighborsClassifier())]),
param_grid={'model__n_neighbors': array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19])},
scoring='roc_auc')In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
GridSearchCV(cv=10,
estimator=Pipeline(steps=[('dummy',
ColumnTransformer(remainder='passthrough',
transformers=[('dummy',
OneHotEncoder(drop='first',
sparse=False),
Index(['job', 'marital', 'education', 'default', 'housing', 'loan', 'contact', 'month', 'day_of_week', 'poutcome'], dtype='object'))],
verbose_feature_names_out=False)),
('normalize', MinMaxScaler()),
('zv', VarianceThreshold()),
('model', KNeighborsClassifier())]),
param_grid={'model__n_neighbors': array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19])},
scoring='roc_auc')Pipeline(steps=[('dummy',
ColumnTransformer(remainder='passthrough',
transformers=[('dummy',
OneHotEncoder(drop='first',
sparse=False),
Index(['job', 'marital', 'education', 'default', 'housing', 'loan', 'contact', 'month', 'day_of_week', 'poutcome'], dtype='object'))],
verbose_feature_names_out=False)),
('normalize', MinMaxScaler()), ('zv', VarianceThreshold()),
('model', KNeighborsClassifier())])ColumnTransformer(remainder='passthrough',
transformers=[('dummy',
OneHotEncoder(drop='first', sparse=False),
Index(['job', 'marital', 'education', 'default', 'housing', 'loan', 'contact', 'month', 'day_of_week', 'poutcome'], dtype='object'))],
verbose_feature_names_out=False)Index(['job', 'marital', 'education', 'default', 'housing', 'loan', 'contact', 'month', 'day_of_week', 'poutcome'], dtype='object')
OneHotEncoder(drop='first', sparse=False)
['age', 'campaign', 'pdays', 'previous', 'emp.var.rate', 'cons.price.idx', 'cons.conf.idx', 'euribor3m', 'nr.employed']
passthrough
MinMaxScaler()
VarianceThreshold()
KNeighborsClassifier()
{'model__n_neighbors': 19}0.7583868296985286yhat=grid.predict(data_bank_marketing_test)
roc_plot(data_bank_marketing_test, y_test, fitted_model, 'yes')0.7583868296985286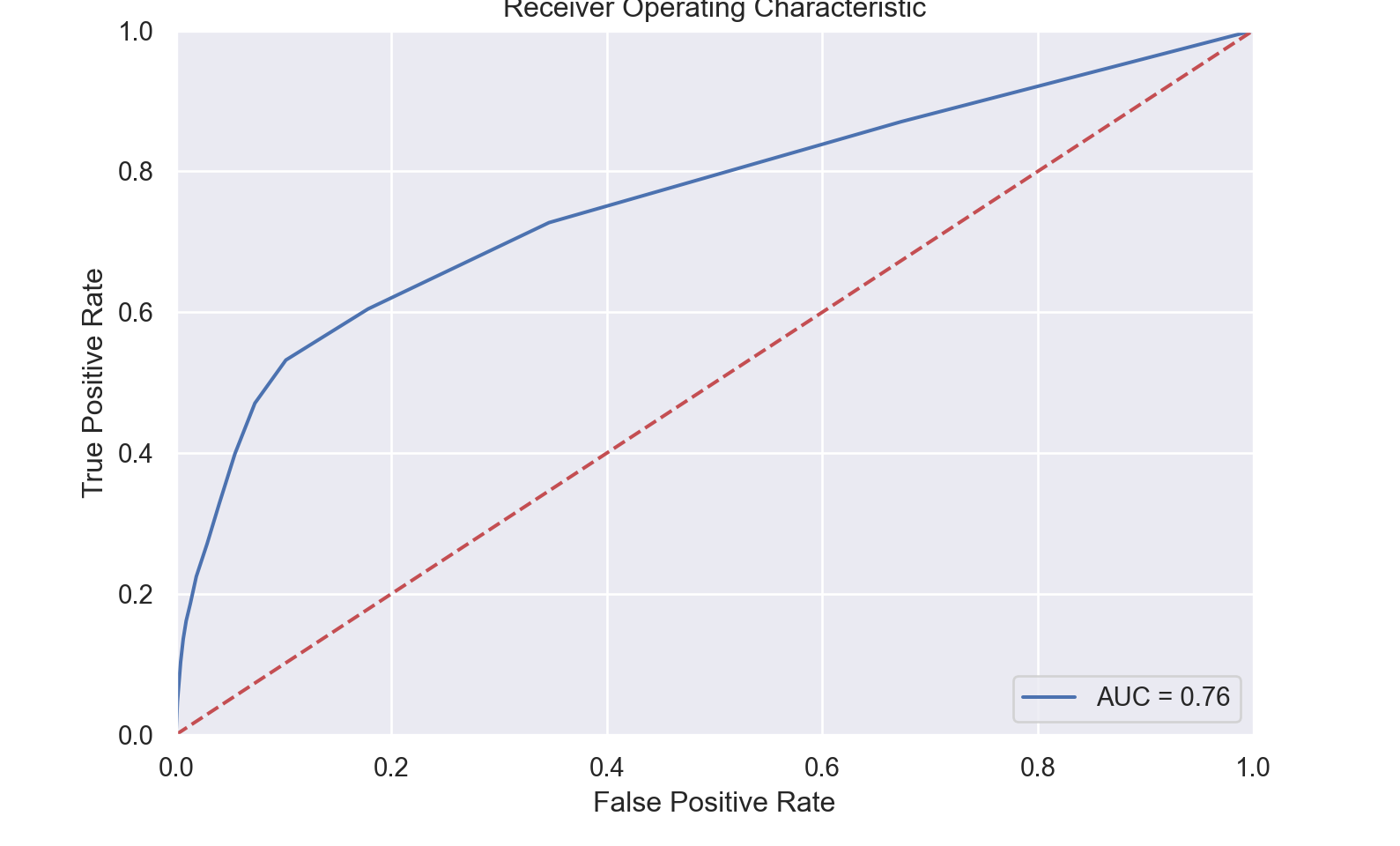
import NearestNeighborModels
KNNClassifier = @load KNNClassifier pkg=NearestNeighborModels verbosity=0NearestNeighborModels.KNNClassifierProbabilisticPipeline(
standardizer = Standardizer(
features = Symbol[],
ignore = false,
ordered_factor = false,
count = false),
continuous_encoder = ContinuousEncoder(
drop_last = false,
one_hot_ordered_factors = false),
knn_classifier = KNNClassifier(
K = 5,
algorithm = :kdtree,
metric = Distances.Euclidean(0.0),
leafsize = 10,
reorder = true,
weights = NearestNeighborModels.Uniform()),
cache = true)
mach = machine(model, X_train, y_train);
fit!(mach);
yhat=MLJ.predict(mach, X_test);
rep = report(mach);
print(
"Measurements:\n",
" brier loss: ", brier_loss(yhat,y_test) |> mean, "\n",
" auc: ", auc(yhat,y_test), "\n",
" accuracy: ", accuracy(mode.(yhat), y_test)
)Measurements:
brier loss: 0.1816056976367755
auc: 0.7262961939438142
accuracy: 0.8910650696018129svm_spec = svm_rbf(cost = 1, margin = 0.1) %>%
set_mode("classification") %>%
set_engine("kernlab")
base_rec = recipe(y ~ ., data = data_bank_marketing_train) %>% step_rm(duration) %>%
step_zv(all_numeric_predictors()) %>%
step_normalize(all_numeric_predictors())
svm_rec = base_rec %>%
step_dummy(all_nominal_predictors())
svm_data = prep(svm_rec, data_bank_marketing_train) %>% bake(new_data = NULL)
svm_wrkflw = workflow() %>% add_model(svm_spec) %>% add_recipe(svm_rec)
svm_wrkflw══ Workflow ════════════════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: svm_rbf()
── Preprocessor ────────────────────────────────────────────────────────────────
4 Recipe Steps
• step_rm()
• step_zv()
• step_normalize()
• step_dummy()
── Model ───────────────────────────────────────────────────────────────────────
Radial Basis Function Support Vector Machine Model Specification (classification)
Main Arguments:
cost = 1
margin = 0.1
Computational engine: kernlab grid_ctrl <-
control_grid (
save_pred = TRUE,
parallel_over = "everything",
save_workflow = TRUE
)
final_svm_fit = svm_wrkflw %>% fit(data=data_bank_marketing_train)
final_svm_pred = final_svm_fit %>% predict(data_bank_marketing_test, type = "prob")
final_svm_pred = final_svm_pred %>% cbind(data_bank_marketing_test %>% select(y))
final_svm_pred$y = as.factor(final_svm_pred$y)
final_svm_pred %>% roc_curve(y, .pred_no) %>% autoplot()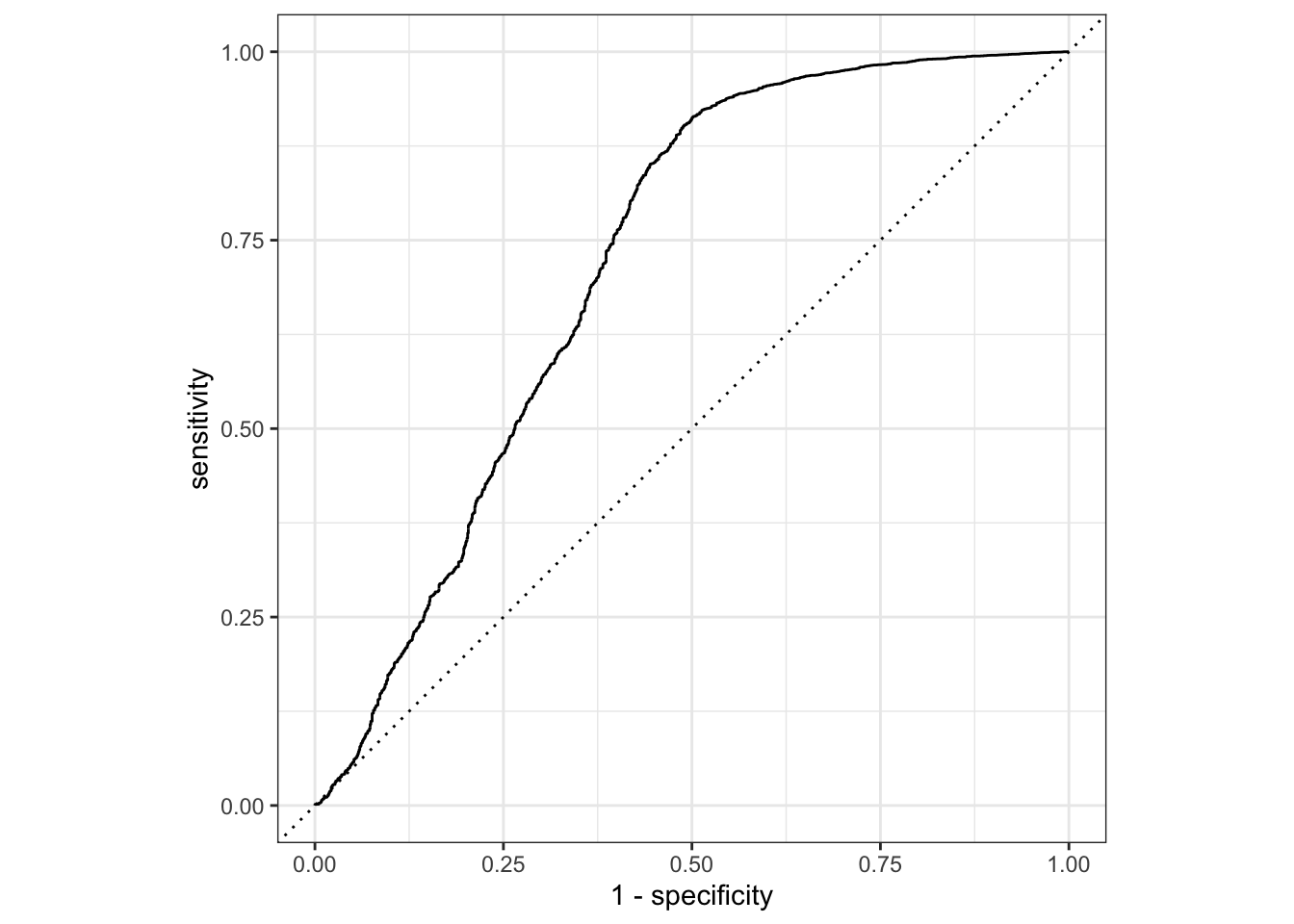
# Cross validation\ grid search is not used for SVC as it is too slow due to the 40K+ observations and 19 features.
model = SVC(kernel='rbf', C=1, gamma = 0.1, probability=True)
# Remove the previous model; the pipeline in this case is used only for data transformation and not model fitting
steps.pop()
# transform train data('model', KNeighborsClassifier())X_trans_train = pipe.fit_transform(data_bank_marketing_train, y_train)
# transform y
label_encoder = LabelEncoder()
y_trans_train = label_encoder.fit_transform(y_train)
y_trans_test = label_encoder.fit_transform(y_test)
# model needs to be fit first due to 'prefit' option used for CalibratedClassifierCV
model.fit(X_trans_train, y_trans_train)
# CalibratedClassifierCV is used to find probabilities, and not for cross validationSVC(C=1, gamma=0.1, probability=True)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
SVC(C=1, gamma=0.1, probability=True)
calibrated_clf = CalibratedClassifierCV(model, cv = 'prefit')
# fit again to find probabilities
calibrated_clf.fit(X_trans_train, y_trans_train)CalibratedClassifierCV(cv='prefit',
estimator=SVC(C=1, gamma=0.1, probability=True))In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
CalibratedClassifierCV(cv='prefit',
estimator=SVC(C=1, gamma=0.1, probability=True))SVC(C=1, gamma=0.1, probability=True)
SVC(C=1, gamma=0.1, probability=True)
array([[0.9119843 , 0.0880157 ],
[0.9120593 , 0.0879407 ],
[0.91198241, 0.08801759],
...,
[0.91272997, 0.08727003],
[0.9137733 , 0.0862267 ],
[0.91701637, 0.08298363]])X_trans_test = pipe.fit_transform(data_bank_marketing_test, y_test)
yhat = calibrated_clf.predict(X_trans_test)
report=metrics.classification_report(y_trans_test,yhat)
print(report) precision recall f1-score support
0 0.91 0.99 0.94 9139
1 0.65 0.19 0.29 1158
accuracy 0.90 10297
macro avg 0.78 0.59 0.62 10297
weighted avg 0.88 0.90 0.87 102970.71219394910423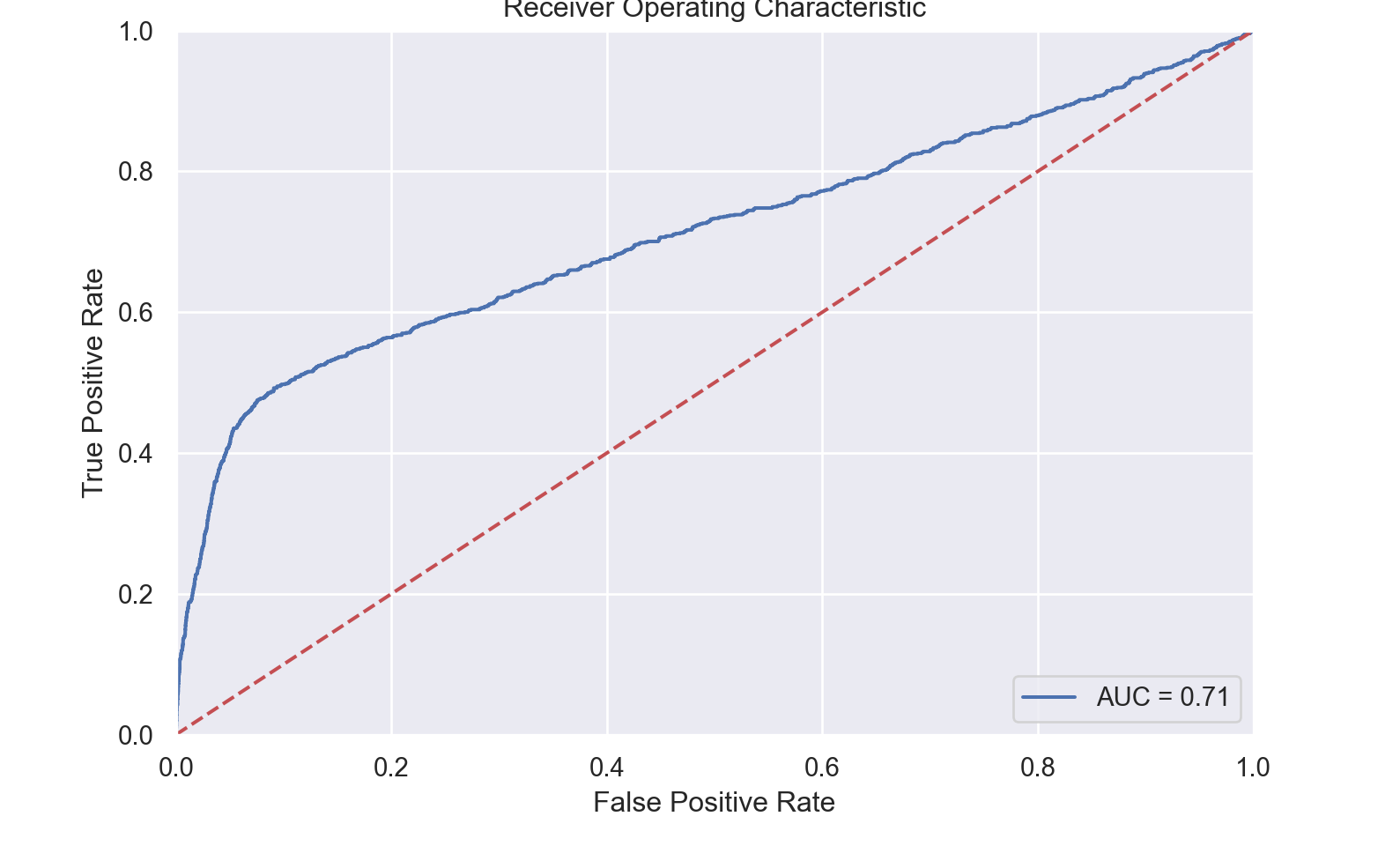
import LIBSVM
#doc("ProbabilisticSVC", pkg="LIBSVM")
ProbabilisticSVC = @load ProbabilisticSVC pkg=LIBSVM verbosity=0MLJLIBSVMInterface.ProbabilisticSVC
model = Standardizer |> ContinuousEncoder |> ProbabilisticSVC(kernel=LIBSVM.Kernel.RadialBasis, gamma = 0.1)ProbabilisticPipeline(
standardizer = Standardizer(
features = Symbol[],
ignore = false,
ordered_factor = false,
count = false),
continuous_encoder = ContinuousEncoder(
drop_last = false,
one_hot_ordered_factors = false),
probabilistic_svc = ProbabilisticSVC(
kernel = LIBSVM.Kernel.RadialBasis,
gamma = 0.1,
cost = 1.0,
cachesize = 200.0,
degree = 3,
coef0 = 0.0,
tolerance = 0.001,
shrinking = true),
cache = true)
mach = machine(model, X_train, y_train);
fit!(mach);
yhat=MLJ.predict(mach, X_test);
rep = report(mach);
print(
"Measurements:\n",
" brier loss: ", brier_loss(yhat,y_test) |> mean, "\n",
" auc: ", auc(yhat,y_test), "\n",
" accuracy: ", accuracy(mode.(yhat), y_test)
)Measurements:
brier loss: 0.16360023292036047
auc: 0.7202998911144449
accuracy: 0.901181612172224xgboost_recipe =
recipe(formula = y ~ ., data = data_bank_marketing_train) %>%
step_rm(duration) %>%
## For modeling, it is preferred to encode qualitative data as factors
## (instead of character).
step_string2factor(one_of("job", "marital", "education", "default", "housing",
"loan", "contact", "month", "day_of_week", "poutcome", "y")) %>%
step_novel(all_nominal_predictors()) %>%
## This model requires the predictors to be numeric. The most common
## method to convert qualitative predictors to numeric is to create
## binary indicator variables (aka dummy variables) from these
## predictors. However, for this model, binary indicator variables can be
## made for each of the levels of the factors (known as 'one-hot
## encoding').
step_dummy(all_nominal_predictors(), one_hot = TRUE) %>%
step_zv(all_predictors())
xgboost_spec =
boost_tree(trees = tune(), tree_depth = tune(), learn_rate = tune(), loss_reduction = tune(), min_n = tune(), sample_size = tune()) %>%
set_mode("classification") %>%
set_engine("xgboost")
xgboost_workflow =
workflow() %>%
add_recipe(xgboost_recipe) %>%
add_model(xgboost_spec)
xgboost_param <- extract_parameter_set_dials(xgboost_spec)
set.seed(87274)
final_params <-
tibble(
trees = 1453,
tree_depth = 11,
learn_rate = 0.052975,
loss_reduction = 7.733554,
min_n = 26,
sample_size = 0.9654255
)
final_xgboost_wflow = xgboost_workflow %>% finalize_workflow(final_params)
final_xgboost_wflow══ Workflow ════════════════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: boost_tree()
── Preprocessor ────────────────────────────────────────────────────────────────
5 Recipe Steps
• step_rm()
• step_string2factor()
• step_novel()
• step_dummy()
• step_zv()
── Model ───────────────────────────────────────────────────────────────────────
Boosted Tree Model Specification (classification)
Main Arguments:
trees = 1453
min_n = 26
tree_depth = 11
learn_rate = 0.052975
loss_reduction = 7.733554
sample_size = 0.9654255
Computational engine: xgboost final_xgboost_fit = final_xgboost_wflow %>% last_fit(data_bank_marketing_split)
final_xgboost_fit %>% collect_metrics()# A tibble: 2 × 4
.metric .estimator .estimate .config
<chr> <chr> <dbl> <chr>
1 accuracy binary 0.901 Preprocessor1_Model1
2 roc_auc binary 0.816 Preprocessor1_Model1# A tibble: 10,297 × 7
id .pred_no .pred_yes .row .pred_class y .config
<chr> <dbl> <dbl> <int> <fct> <fct> <chr>
1 train/test split 0.971 0.0286 7 no no Preprocessor1_Mo…
2 train/test split 0.973 0.0274 18 no no Preprocessor1_Mo…
3 train/test split 0.974 0.0257 21 no no Preprocessor1_Mo…
4 train/test split 0.978 0.0222 22 no no Preprocessor1_Mo…
5 train/test split 0.970 0.0305 24 no no Preprocessor1_Mo…
6 train/test split 0.979 0.0212 30 no no Preprocessor1_Mo…
7 train/test split 0.977 0.0230 34 no no Preprocessor1_Mo…
8 train/test split 0.976 0.0240 35 no no Preprocessor1_Mo…
9 train/test split 0.973 0.0267 43 no no Preprocessor1_Mo…
10 train/test split 0.979 0.0210 52 no no Preprocessor1_Mo…
# … with 10,287 more rows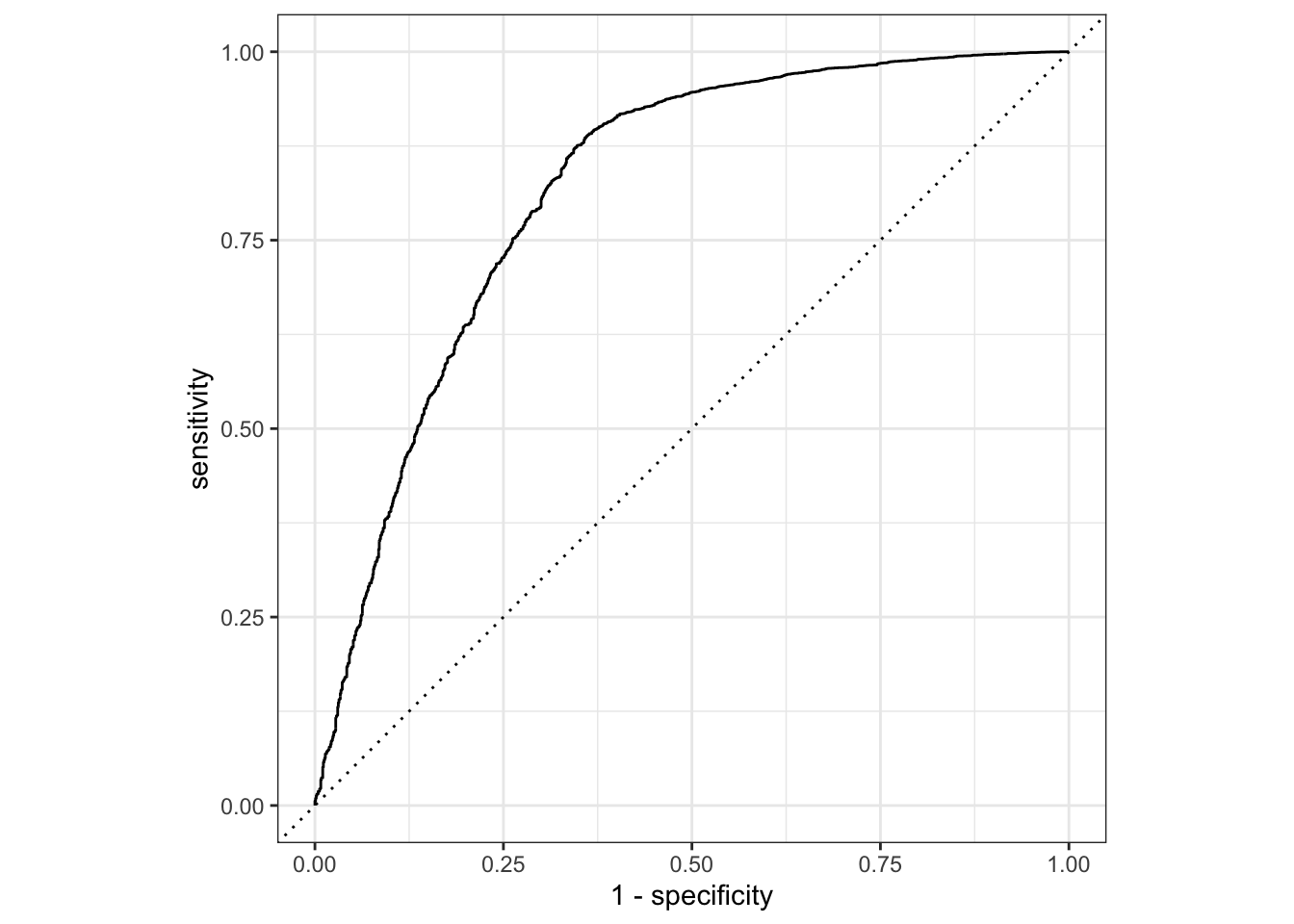
from sklearn.model_selection import StratifiedKFold
from xgboost import XGBClassifier
def grid_search_xgb(params, X, y, kfold, random=False):
xgb = XGBClassifier(booster='gbtree', objective='binary:logistic', random_state=2)
if random:
grid = RandomizedSearchCV(xgb, params, cv=kfold, n_iter=10, n_jobs=-1, scoring='roc_auc') #n_iter controls number of random combinations
else:
grid = GridSearchCV(xgb, params, cv=kfold,n_jobs=-1, scoring='roc_auc')
grid.fit(X, y)
print('Best params:', grid.best_params_)
print('Best score:', grid.best_score_)
#
#
st_Kfold = StratifiedKFold(n_splits=5, shuffle=True, random_state=2)
#
# #n_estimators is the number of trees trained, default is 100. 7 seems to be an optimum value.
# params={'n_estimators':[7,10]}
# grid_search_xgb(params, X_trans_train, y_trans_train, st_Kfold)
#
# #learning_rate shrinks the weights of trees for each round of boosting, default is 0.3. By lowering learning_rate, more trees are required to produce better scores. Lowering learning_rate prevents overfitting because the size of the weights carried forward is smaller. 0.05 seems to be an optimum value.
# params={'learning_rate':[0.01, 0.05, 0.075, 0.1, 0.2, 0.3, 0.4, 0.5]}
# grid_search_xgb(params, X_trans_train, y_trans_train, st_Kfold)
#
# #max_depth determines the length of the tree, equivalent to the number of rounds of splitting. default is 6. Limiting max_depth prevents overfitting because the individual trees can only grow as far as max_depth allows. 2 seems to be an optimum value.
# params={'max_depth':[1,2, 3, 5, 6, 8]}
# grid_search_xgb(params, X_trans_train, y_trans_train, st_Kfold)
#
# #gamma provides a threshold that nodes must surpass before making further splits according to the loss function, default is 0.There is no upper limit to the value of gamma. Anything over 10 is considered very high. Increasing gamma results in a more conservative model. 5 seems to be an optimum value.
# params={'gamma':[0, 0.1, 0.5, 1, 2, 5, 7]}
# grid_search_xgb(params, X_trans_train, y_trans_train, st_Kfold)
#
# #min_child_weight refers to the minimum sum of weights required for a node to split into a child. If the sum of the weights is less than the value of min_child_weight, no further splits are made.min_child_weight reduces overfitting by increasing its value. 4 seems to be an optimum value.
# params={'min_child_weight':[1, 2, 3, 4, 5]}
# grid_search_xgb(params, X_trans_train, y_trans_train, st_Kfold)
#
# #The subsample hyperparameter limits the percentage of training instances (rows) for each boosting round. Decreasing subsample from 100% reduces overfitting. 1 seems to be an optimum value:
# params={'subsample':[0.5, 0.7, 0.8, 0.9, 1]}
# grid_search_xgb(params, X_trans_train, y_trans_train, st_Kfold)
#
# #colsample_bytree randomly selects particular columnsaccording to the given percentage.colsample_bytree is useful for limiting the influence of columns and reducing variance. 0.7 seems to be an optimum value.
# params={'colsample_bytree':[0.5, 0.7, 0.8, 0.9,1]}
# grid_search_xgb(params, X_trans_train, y_trans_train, st_Kfold)
#
#
params={'n_estimators':[5,7,10,20,50],
'learning_rate': [0.05,0.1, 0.2, 0.3, 0.4, 0.5],
'max_depth': [2,4,6],
'gamma': [0.1,0.5,2, 5],
'min_child_weight': [3,4,5],
'subsample': [0.5,1],
'colsample_bytree': [0.5,0.7,1]}
# # ->grid_search_xgb(params, X_trans_train, y_trans_train, st_Kfold)
#
#
# #Output:
# #Best params: {'colsample_bytree': 0.7, 'gamma': 0.1, 'learning_rate': 0.1, 'max_depth': 6, 'min_child_weight': 4, 'n_estimators': 50, 'subsample': 1}
# #Best score: 0.800812151928098
#
#
params={'n_estimators':[20,50,75,100],
'learning_rate': [0.05,0.1, 0.15, 0.2],
'max_depth': [6,8,10],
'gamma': [0.1,0.2,0.3],
'min_child_weight': [3,4,5],
'subsample': [0.75,1],
'colsample_bytree': [0.7,0.8,1]}
#
# # ->grid_search_xgb(params, X_trans_train, y_trans_train, st_Kfold, random=True)
#
# # ->grid_search(params={'subsample':[0.5, 0.6, 0.7, 0.8, 0.9, 1],'min_child_weight':[1, 2, 3, 4, 5],'learning_rate':[0.1, 0.2, 0.3, 0.4, 0.5],'max_depth':[1, 2, 3, 4, 5], 'n_estimators':[2]})
# #Best params: {'subsample': 1, 'n_estimators': 75, 'min_child_weight': 3, 'max_depth': 8, 'learning_rate': 0.05, 'gamma': 0.1, 'colsample_bytree': 0.7}
# #Best score: 0.8013732623090342
#
final_model = XGBClassifier(booster='gbtree',objective='binary:logistic', max_depth=8, learning_rate=0.05, n_estimators=75, subsample=1, min_child_weight=3, gamma=0.1, colsample_bytree=0.7, random_state=2, n_jobs=-1)
#
fitted_model=final_model.fit(X_trans_train, y_trans_train)
print ('ROC AUC Score',roc_plot(X_trans_test,y_trans_test, fitted_model, 1))ROC AUC Score 0.8105681566276057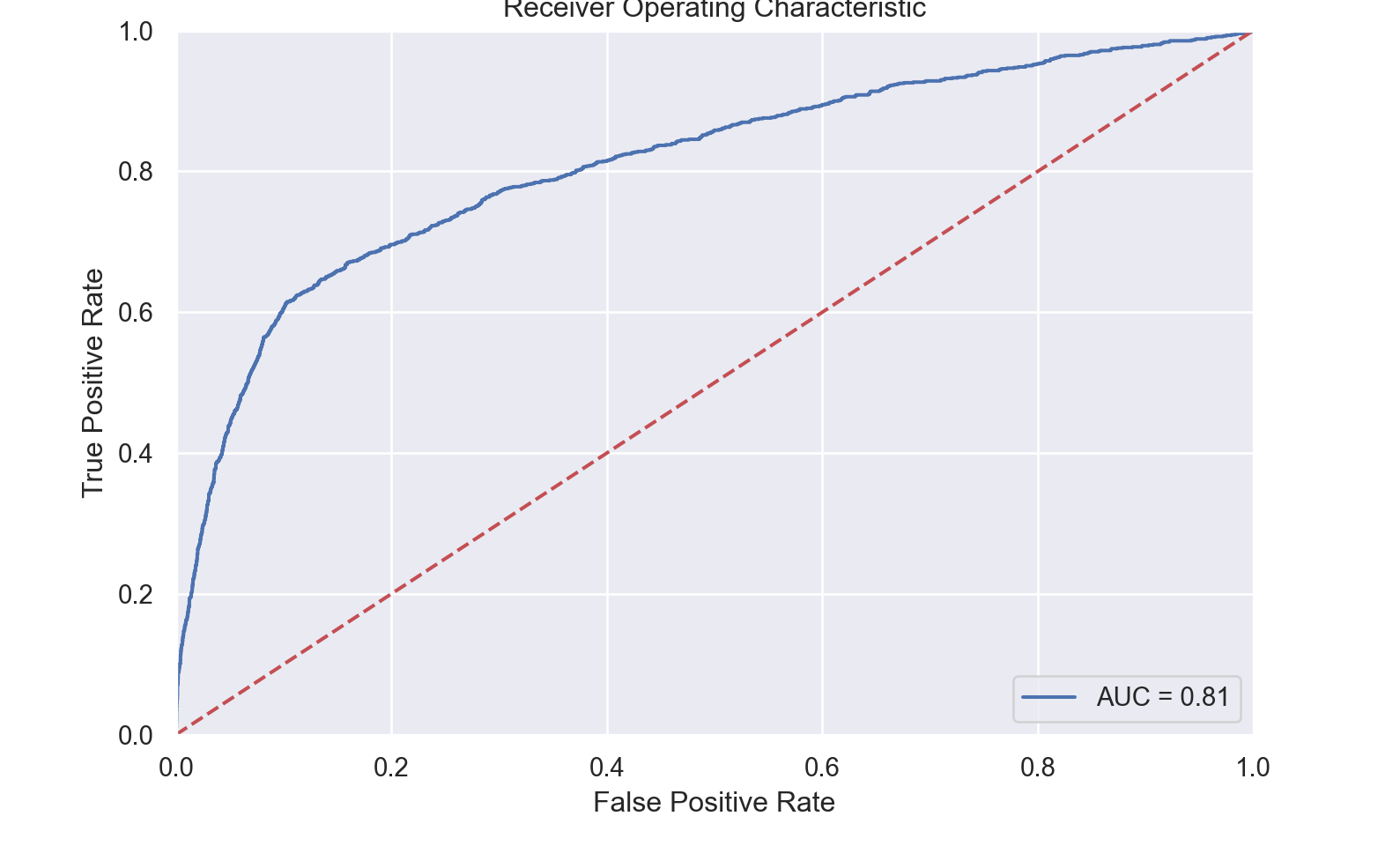
MLJXGBoostInterface.XGBoostClassifierProbabilisticPipeline(
standardizer = Standardizer(
features = Symbol[],
ignore = false,
ordered_factor = false,
count = false),
continuous_encoder = ContinuousEncoder(
drop_last = false,
one_hot_ordered_factors = false),
xg_boost_classifier = XGBoostClassifier(
test = 1,
num_round = 100,
booster = "gbtree",
disable_default_eval_metric = 0,
eta = 0.3,
num_parallel_tree = 1,
gamma = 0.0,
max_depth = 6,
min_child_weight = 1.0,
max_delta_step = 0.0,
subsample = 1.0,
colsample_bytree = 1.0,
colsample_bylevel = 1.0,
colsample_bynode = 1.0,
lambda = 1.0,
alpha = 0.0,
tree_method = "auto",
sketch_eps = 0.03,
scale_pos_weight = 1.0,
updater = nothing,
refresh_leaf = 1,
process_type = "default",
grow_policy = "depthwise",
max_leaves = 0,
max_bin = 256,
predictor = "cpu_predictor",
sample_type = "uniform",
normalize_type = "tree",
rate_drop = 0.0,
one_drop = 0,
skip_drop = 0.0,
feature_selector = "cyclic",
top_k = 0,
tweedie_variance_power = 1.5,
objective = "automatic",
base_score = 0.5,
watchlist = nothing,
nthread = 1,
importance_type = "gain",
seed = nothing,
validate_parameters = false),
cache = true)ProbabilisticPipeline(
standardizer = Standardizer(
features = Symbol[],
ignore = false,
ordered_factor = false,
count = false),
continuous_encoder = ContinuousEncoder(
drop_last = false,
one_hot_ordered_factors = false),
xg_boost_classifier = XGBoostClassifier(
test = 1,
num_round = 100,
booster = "gbtree",
disable_default_eval_metric = 0,
eta = 0.3,
num_parallel_tree = 1,
gamma = 0.0,
max_depth = 6,
min_child_weight = 1.0,
max_delta_step = 0.0,
subsample = 1.0,
colsample_bytree = 1.0,
colsample_bylevel = 1.0,
colsample_bynode = 1.0,
lambda = 1.0,
alpha = 0.0,
tree_method = "auto",
sketch_eps = 0.03,
scale_pos_weight = 1.0,
updater = nothing,
refresh_leaf = 1,
process_type = "default",
grow_policy = "depthwise",
max_leaves = 0,
max_bin = 256,
predictor = "cpu_predictor",
sample_type = "uniform",
normalize_type = "tree",
rate_drop = 0.0,
one_drop = 0,
skip_drop = 0.0,
feature_selector = "cyclic",
top_k = 0,
tweedie_variance_power = 1.5,
objective = "automatic",
base_score = 0.5,
watchlist = nothing,
nthread = 1,
importance_type = "gain",
seed = nothing,
validate_parameters = false),
cache = true)import MLJXGBoostInterface ✔MLJXGBoostInterface.XGBoostClassifierProbabilisticPipeline(
standardizer = Standardizer(
features = Symbol[],
ignore = false,
ordered_factor = false,
count = false),
continuous_encoder = ContinuousEncoder(
drop_last = false,
one_hot_ordered_factors = false),
xg_boost_classifier = XGBoostClassifier(
test = 1,
num_round = 100,
booster = "gbtree",
disable_default_eval_metric = 0,
eta = 0.3,
num_parallel_tree = 1,
gamma = 0.0,
max_depth = 6,
min_child_weight = 1.0,
max_delta_step = 0.0,
subsample = 1.0,
colsample_bytree = 1.0,
colsample_bylevel = 1.0,
colsample_bynode = 1.0,
lambda = 1.0,
alpha = 0.0,
tree_method = "auto",
sketch_eps = 0.03,
scale_pos_weight = 1.0,
updater = nothing,
refresh_leaf = 1,
process_type = "default",
grow_policy = "depthwise",
max_leaves = 0,
max_bin = 256,
predictor = "cpu_predictor",
sample_type = "uniform",
normalize_type = "tree",
rate_drop = 0.0,
one_drop = 0,
skip_drop = 0.0,
feature_selector = "cyclic",
top_k = 0,
tweedie_variance_power = 1.5,
objective = "automatic",
base_score = 0.5,
watchlist = nothing,
nthread = 1,
importance_type = "gain",
seed = nothing,
validate_parameters = false),
cache = true)ProbabilisticPipeline(
standardizer = Standardizer(
features = Symbol[],
ignore = false,
ordered_factor = false,
count = false),
continuous_encoder = ContinuousEncoder(
drop_last = false,
one_hot_ordered_factors = false),
xg_boost_classifier = XGBoostClassifier(
test = 1,
num_round = 100,
booster = "gbtree",
disable_default_eval_metric = 0,
eta = 0.3,
num_parallel_tree = 1,
gamma = 0.0,
max_depth = 6,
min_child_weight = 1.0,
max_delta_step = 0.0,
subsample = 1.0,
colsample_bytree = 1.0,
colsample_bylevel = 1.0,
colsample_bynode = 1.0,
lambda = 1.0,
alpha = 0.0,
tree_method = "auto",
sketch_eps = 0.03,
scale_pos_weight = 1.0,
updater = nothing,
refresh_leaf = 1,
process_type = "default",
grow_policy = "depthwise",
max_leaves = 0,
max_bin = 256,
predictor = "cpu_predictor",
sample_type = "uniform",
normalize_type = "tree",
rate_drop = 0.0,
one_drop = 0,
skip_drop = 0.0,
feature_selector = "cyclic",
top_k = 0,
tweedie_variance_power = 1.5,
objective = "automatic",
base_score = 0.5,
watchlist = nothing,
nthread = 1,
importance_type = "gain",
seed = nothing,
validate_parameters = false),
cache = true)tuning = RandomSearch(rng=123);
eta = range(model,
:(xg_boost_classifier.eta),
lower=0.1,
upper=1,
unit=0.2)NumericRange(0.1 ≤ xg_boost_classifier.eta ≤ 1.0; origin=0.55, unit=0.2)NumericRange(1.0 ≤ xg_boost_classifier.gamma ≤ 6.0; origin=3.5, unit=1.0)NumericRange(1 ≤ xg_boost_classifier.max_depth ≤ 6; origin=3.5, unit=1.0)NumericRange(0.1 ≤ xg_boost_classifier.subsample ≤ 1.0; origin=0.55, unit=0.25)
colsample_bytree = range(model,
:(xg_boost_classifier.colsample_bytree),
lower=0.2,
upper=1,
unit=0.25)NumericRange(0.2 ≤ xg_boost_classifier.colsample_bytree ≤ 1.0; origin=0.6, unit=0.25)
tuned_model = TunedModel(model=model,
ranges=[eta, gamma, max_depth,subsample,colsample_bytree],
resampling=CV(nfolds=10),
measures=auc,
tuning=tuning,
n=50);
mach = machine(tuned_model, X_train, y_train);
fit!(mach);
yhat=MLJ.predict(mach, X_test);
rep = report(mach);
print(
"Measurements:\n",
" brier loss: ", brier_loss(yhat,y_test) |> mean, "\n",
" auc: ", auc(yhat,y_test), "\n",
" accuracy: ", accuracy(mode.(yhat), y_test)
)Measurements:
brier loss: 0.1494576
auc: 0.8101407168755788
accuracy: 0.9040142440919392
#Results for n=50
#brier loss: 0.1494576
#auc: 0.8101407168755788
#accuracy: 0.9040142440919392
println(rep.best_model.xg_boost_classifier.eta) # 0.28359696048424090.28359696048424092.17271837800284930.78377918819096190.35342415963021280.28359696048424092.17271837800284930.78377918819096190.3534241596302128