library(tidyverse)
library(tidymodels)
tidymodels_prefer()
library(kernlab)
library(mlbench)
library(caret)
library(knitr)
library(ggcorrplot)
library(skimr)CPU Performance
Introduction
The data is sourced from the UCI ML Repository and can be downloaded here. It is related to predicting the performance of computers from various brands from the 1980s time frame.
Goal
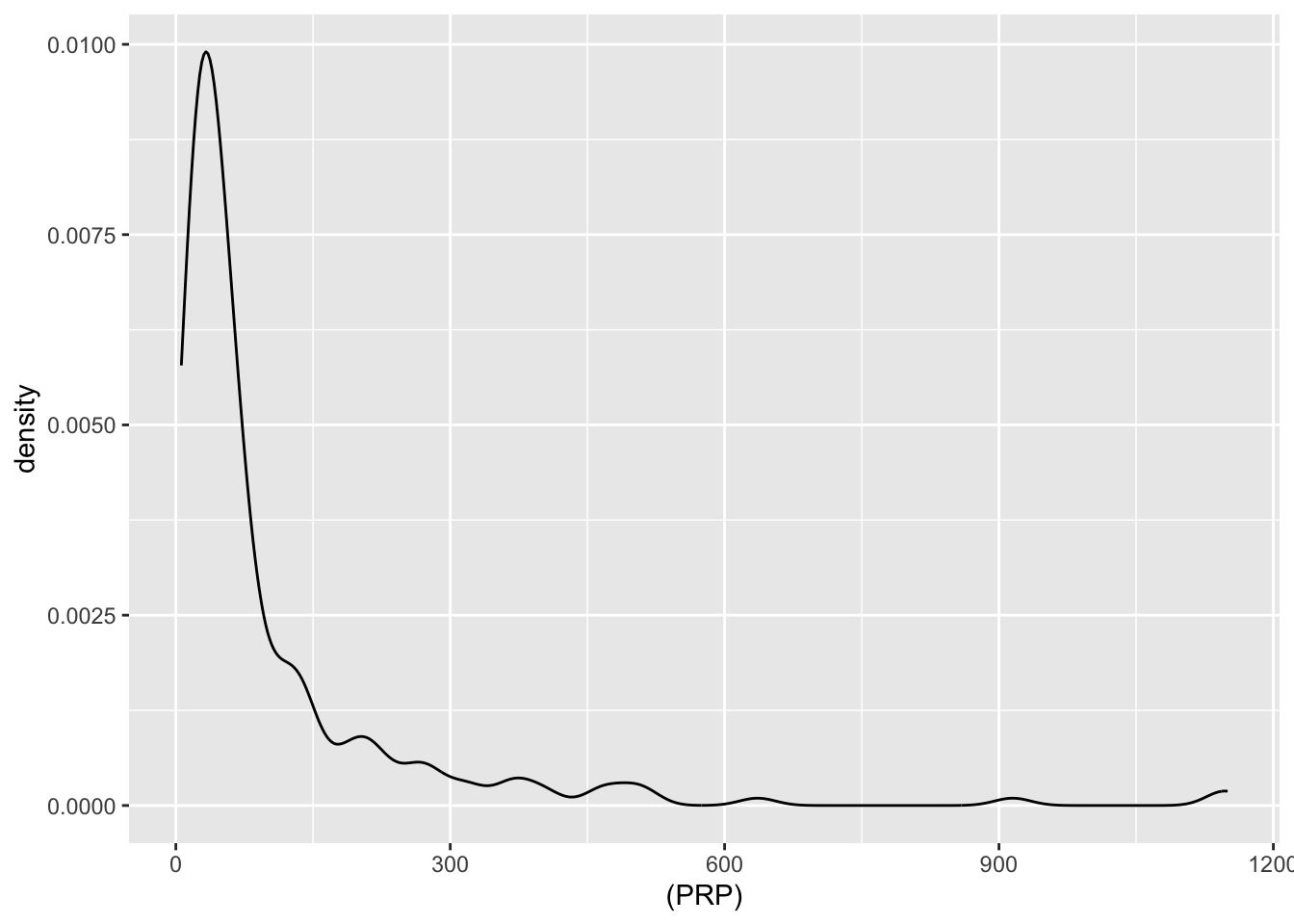
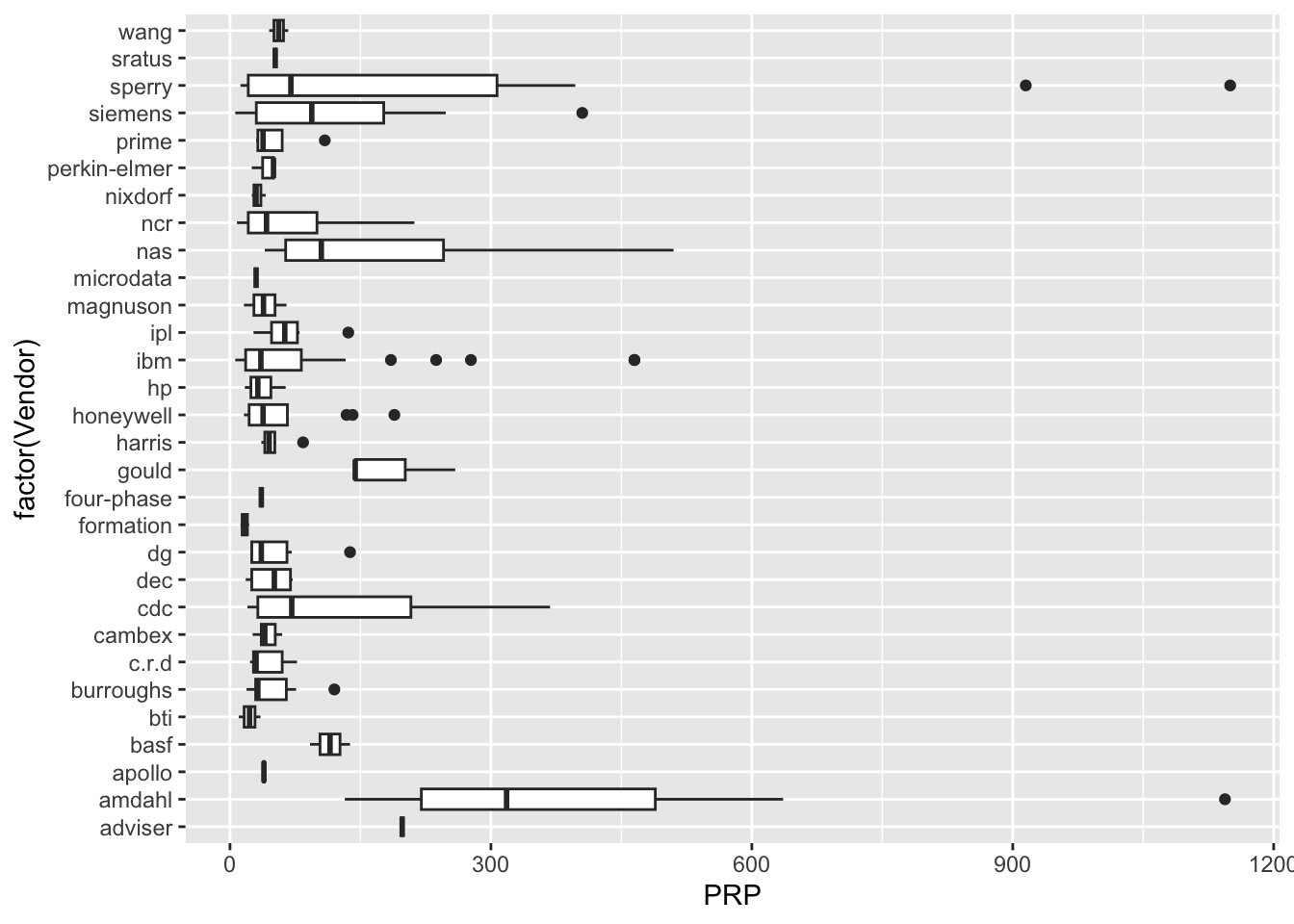
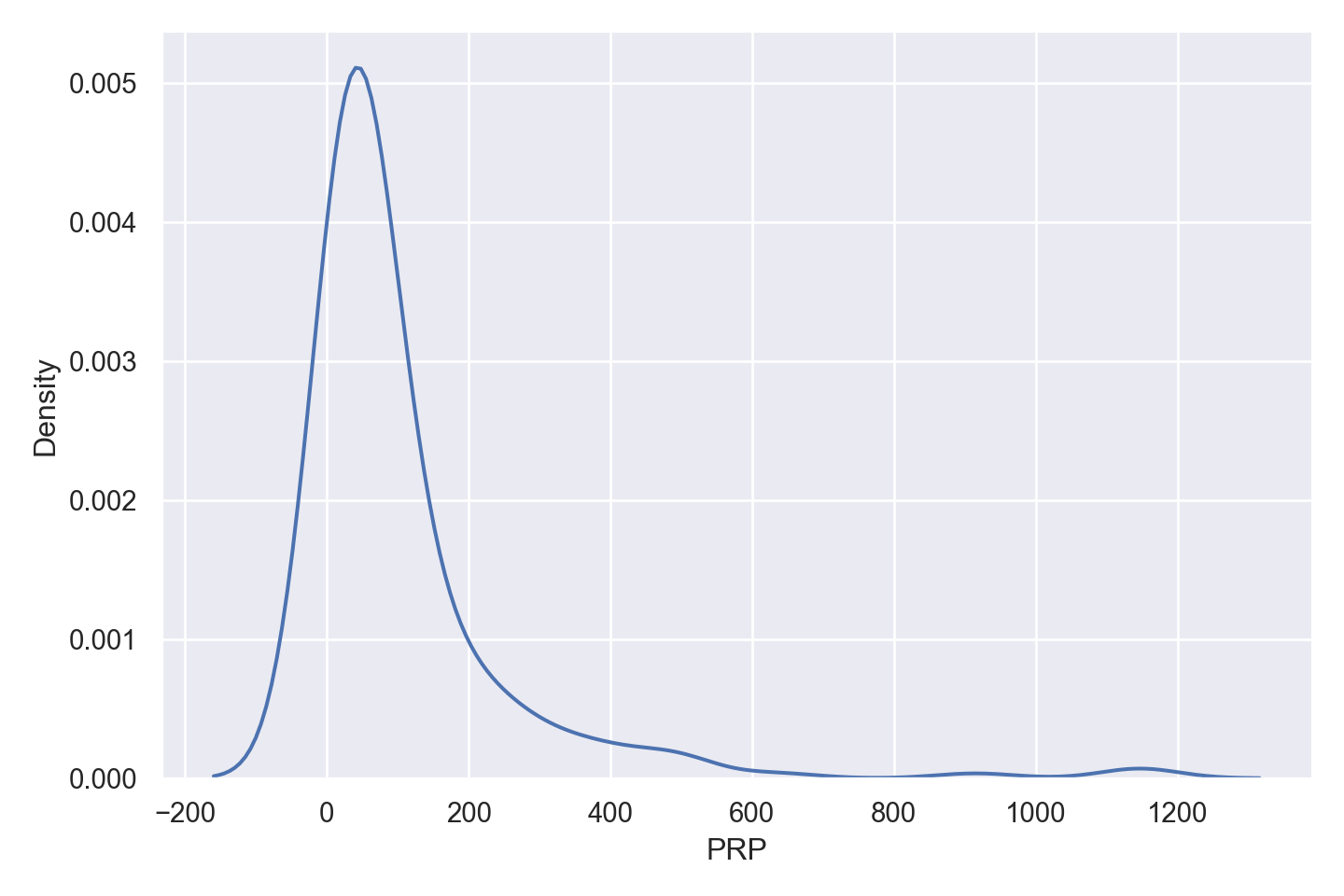
The regression goal is to predict the performance of the computer (variable PRP).
Data Dictionary
| Attribute Name | Type | Description |
|---|---|---|
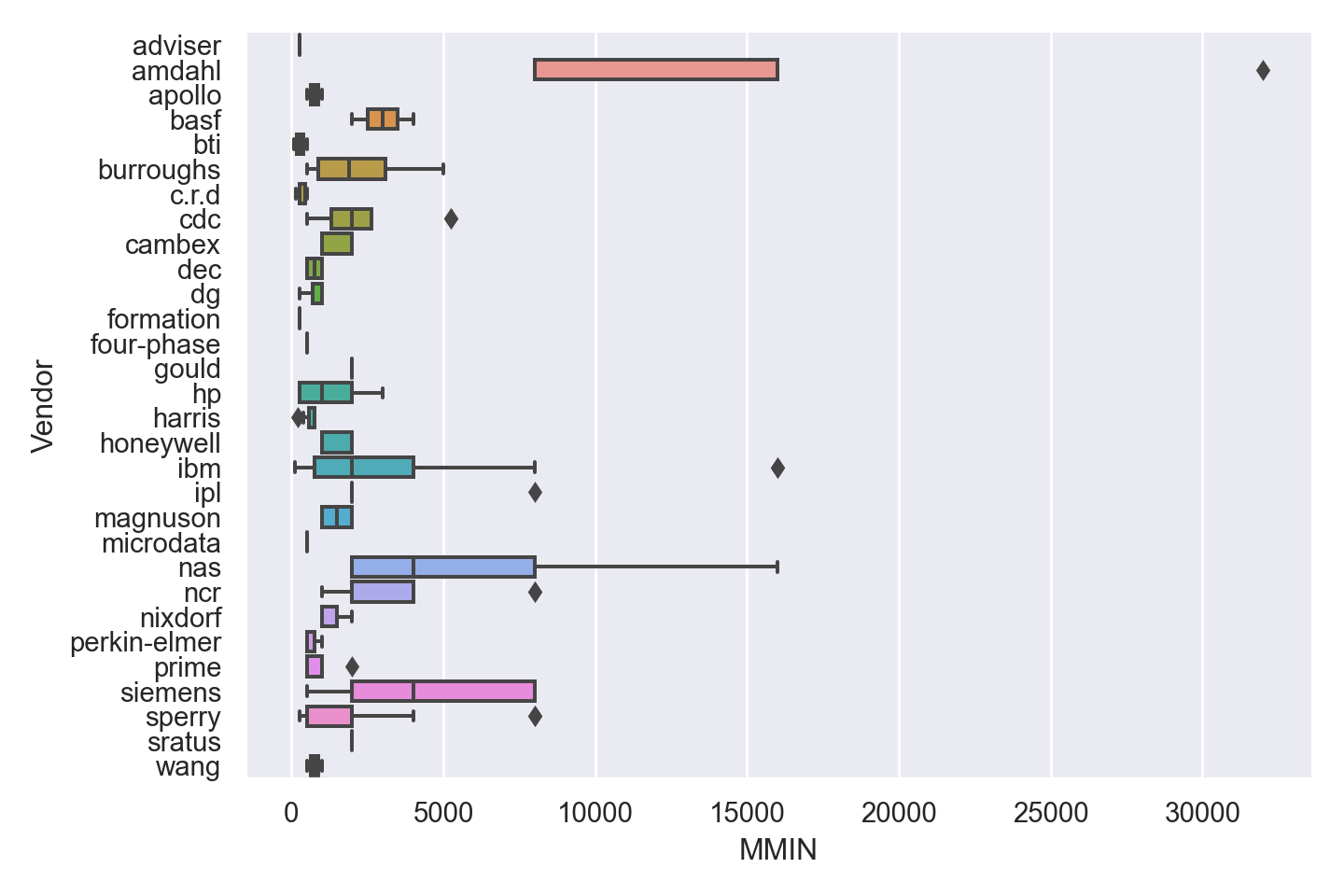
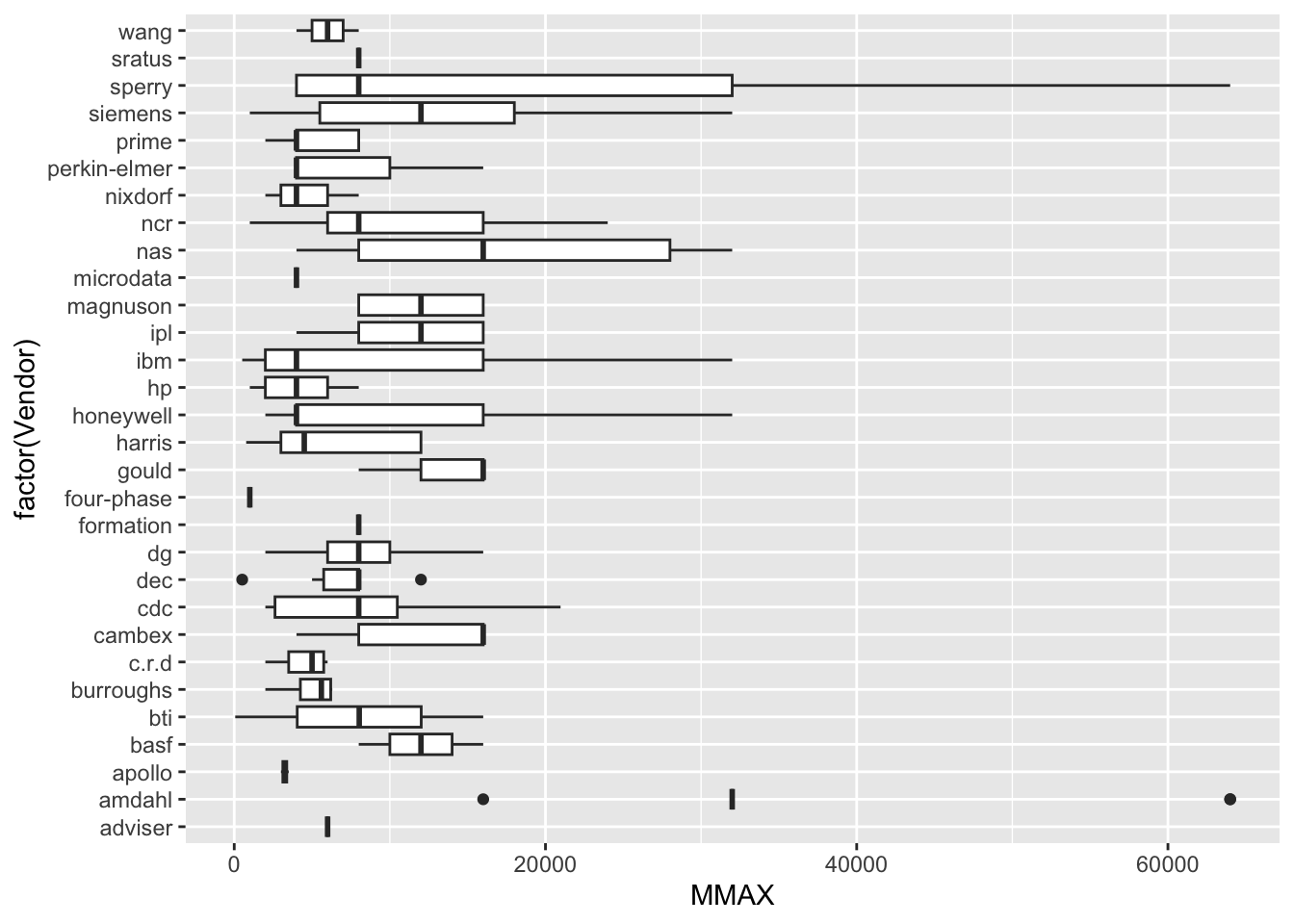
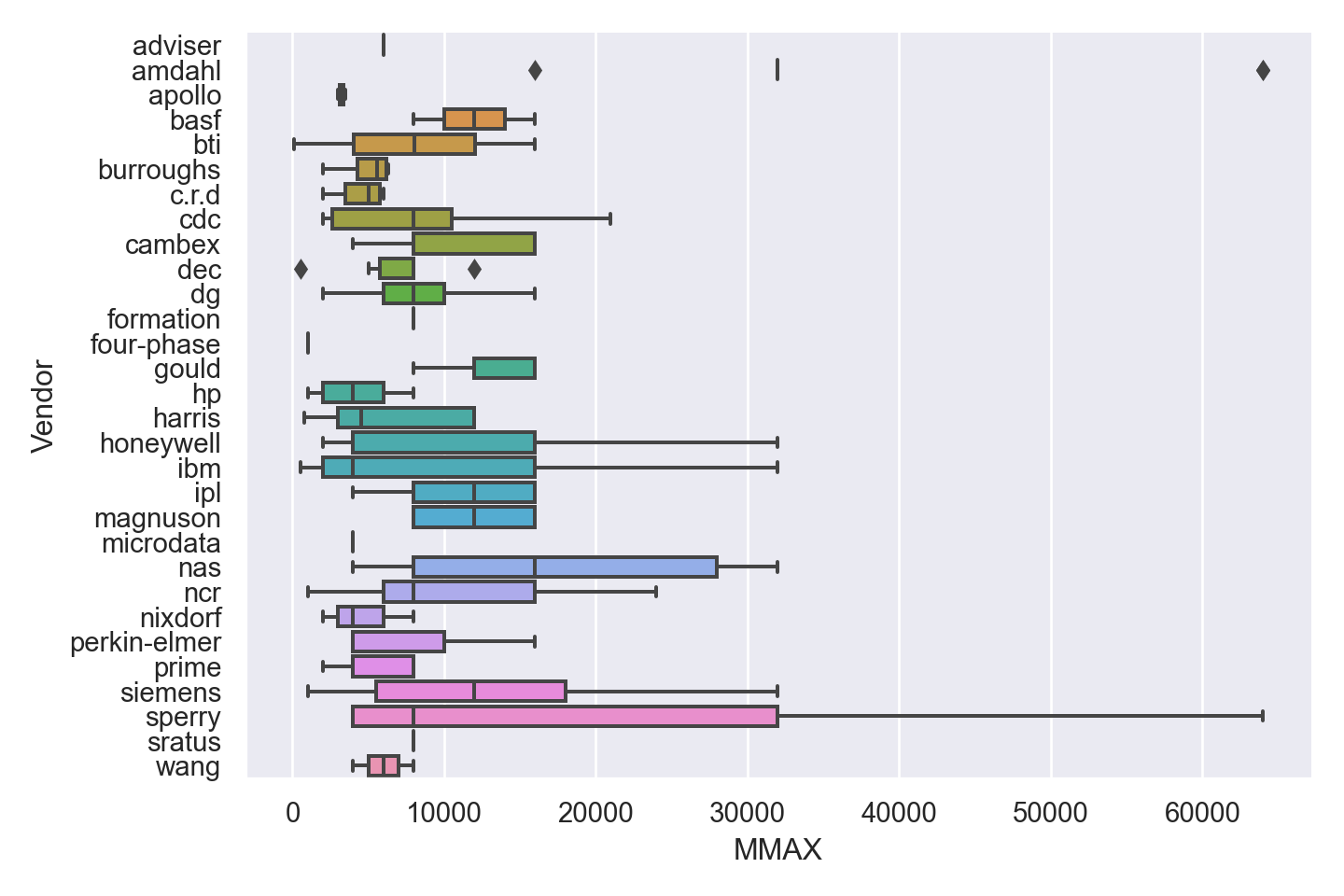
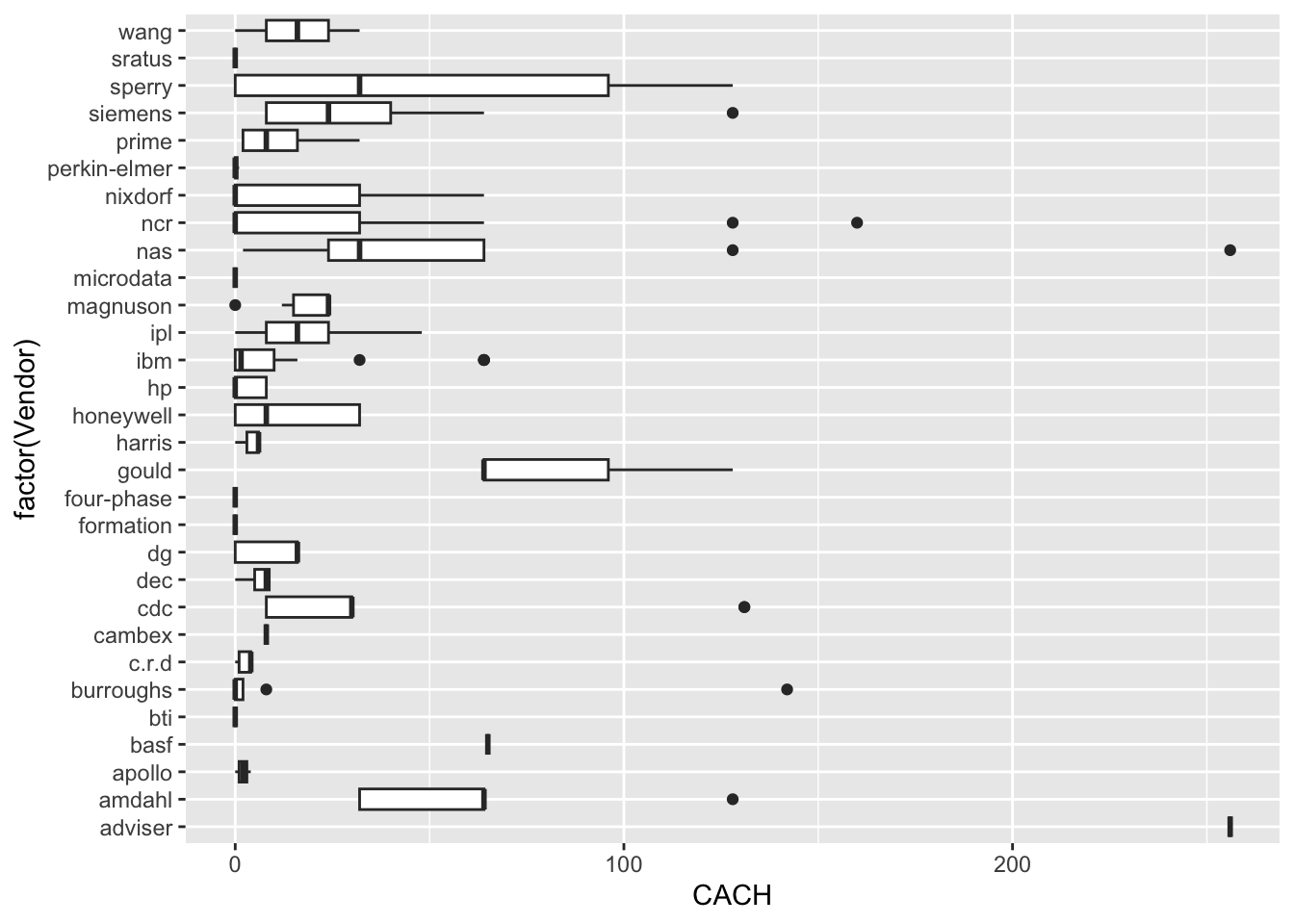
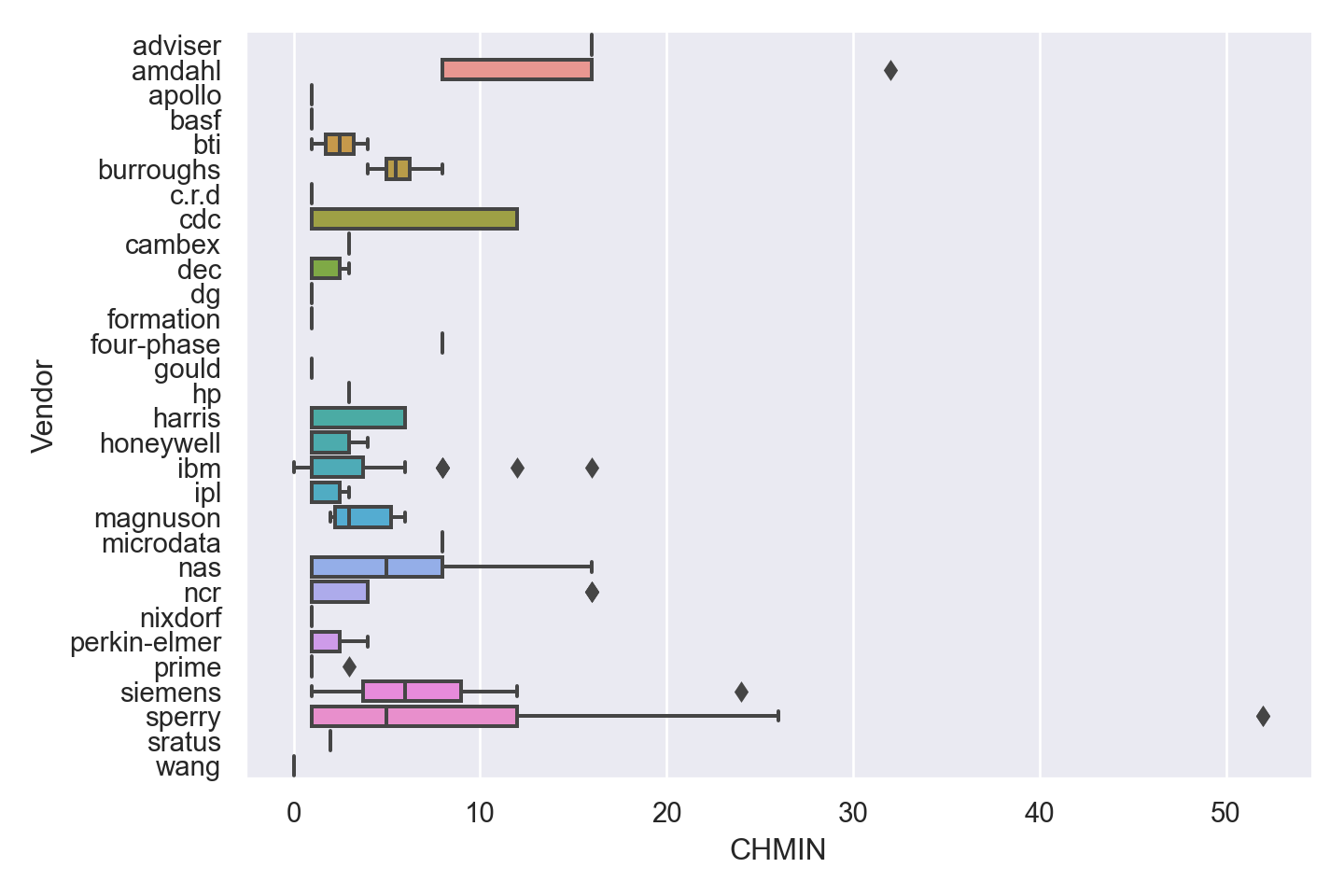
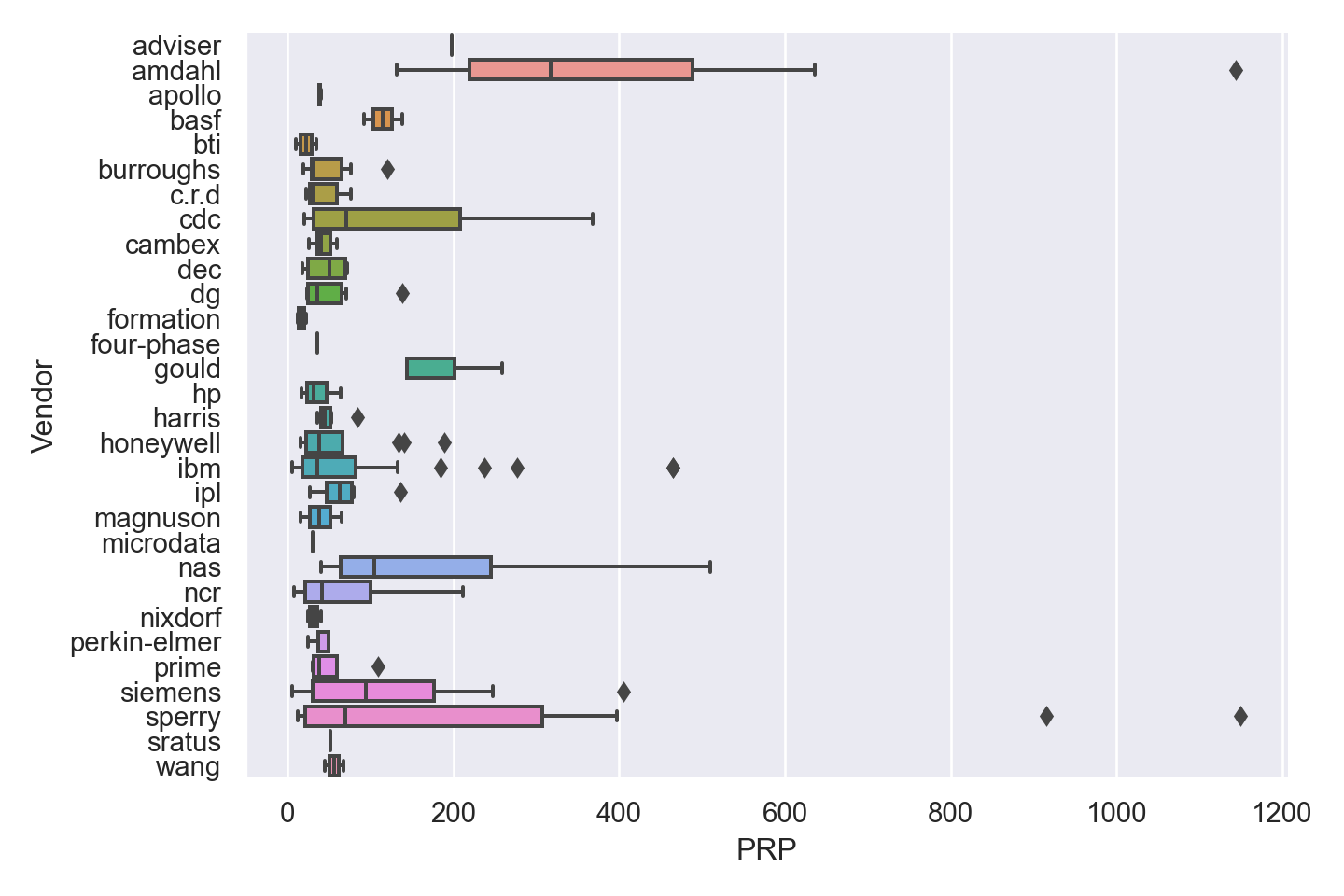
| Vendor | categorical | name of the computer manufacturer |
| Model Name | categorical | name of the model |
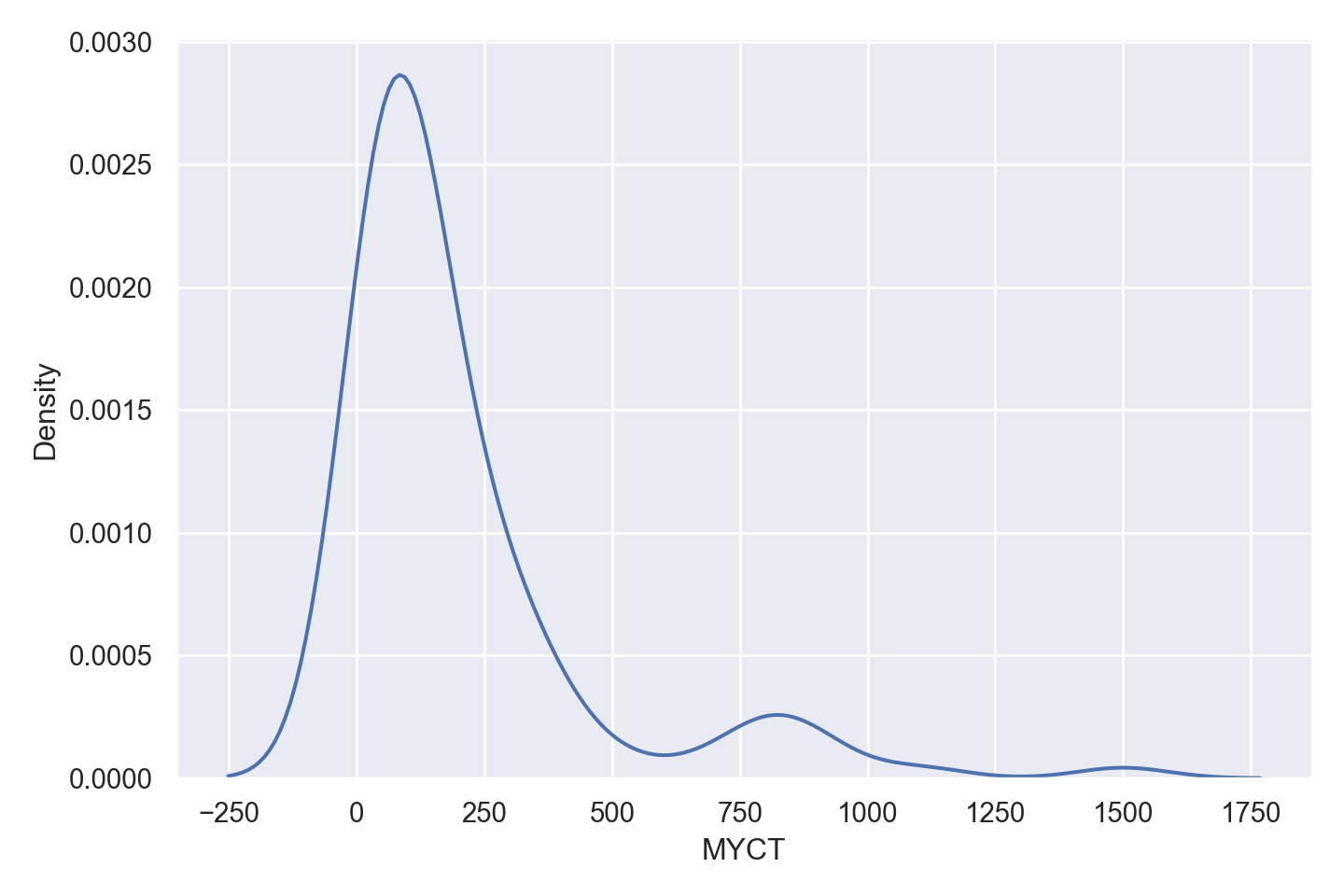
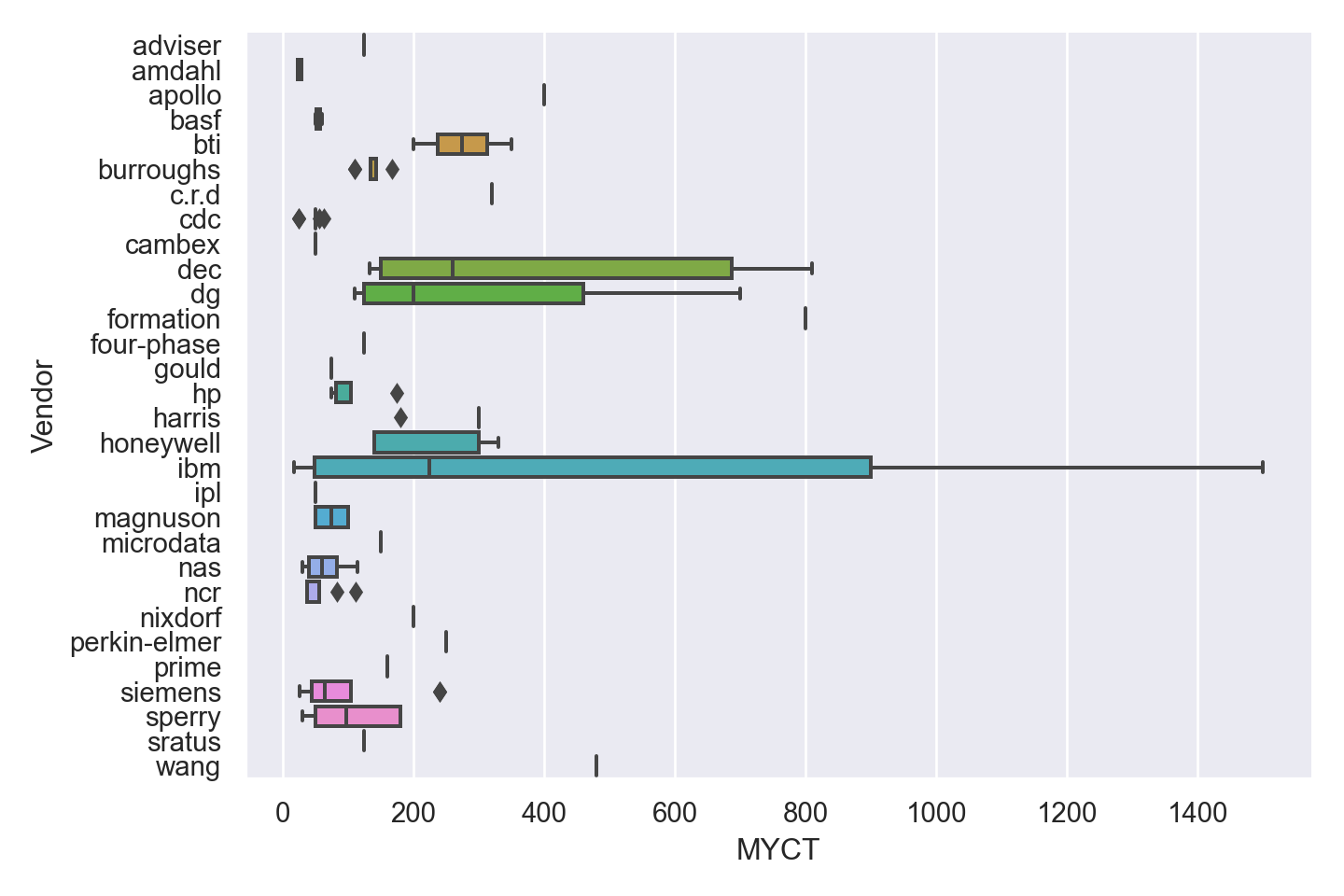
| MYCT | numeric | machine cycle time in nanoseconds (integer) |
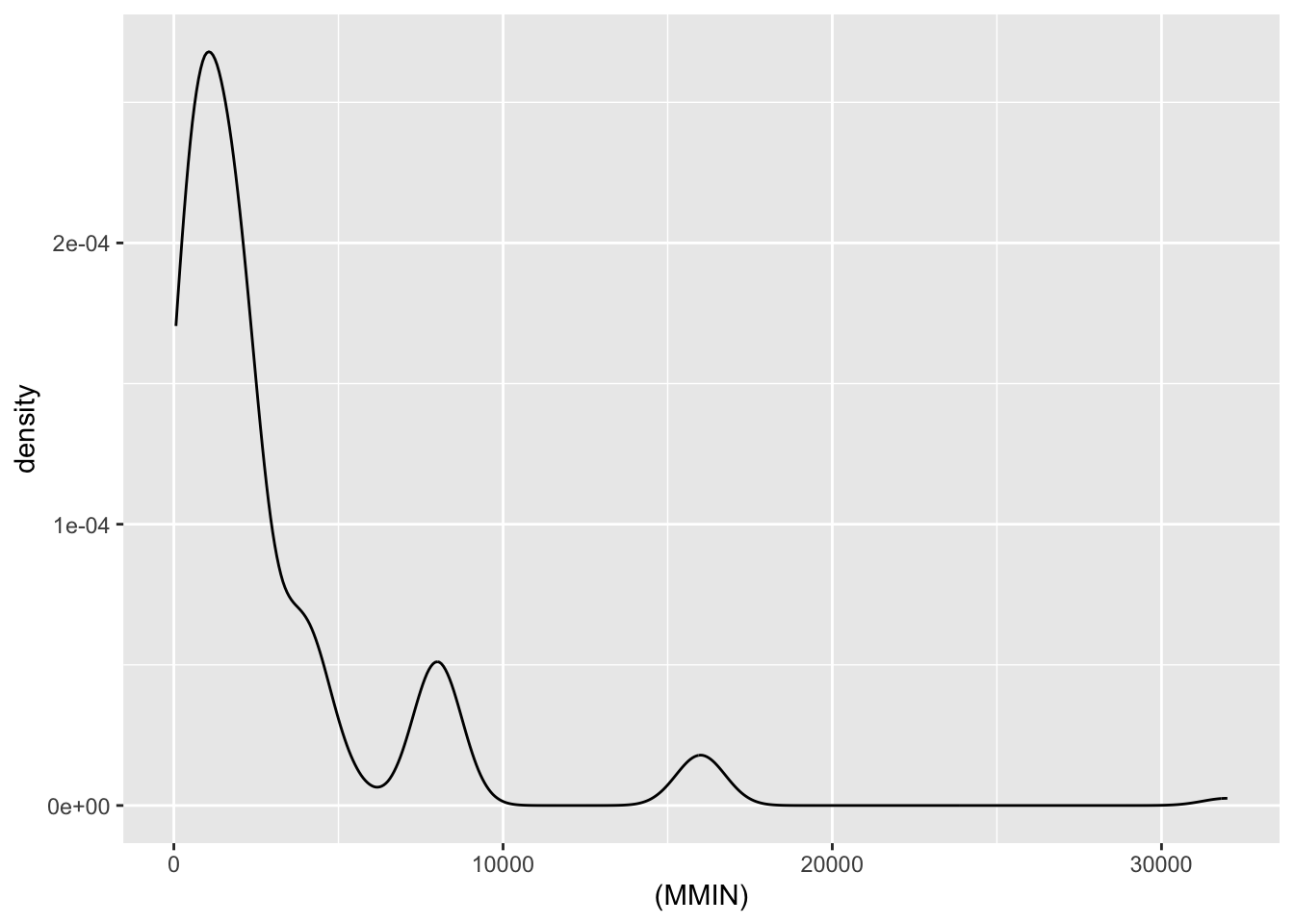
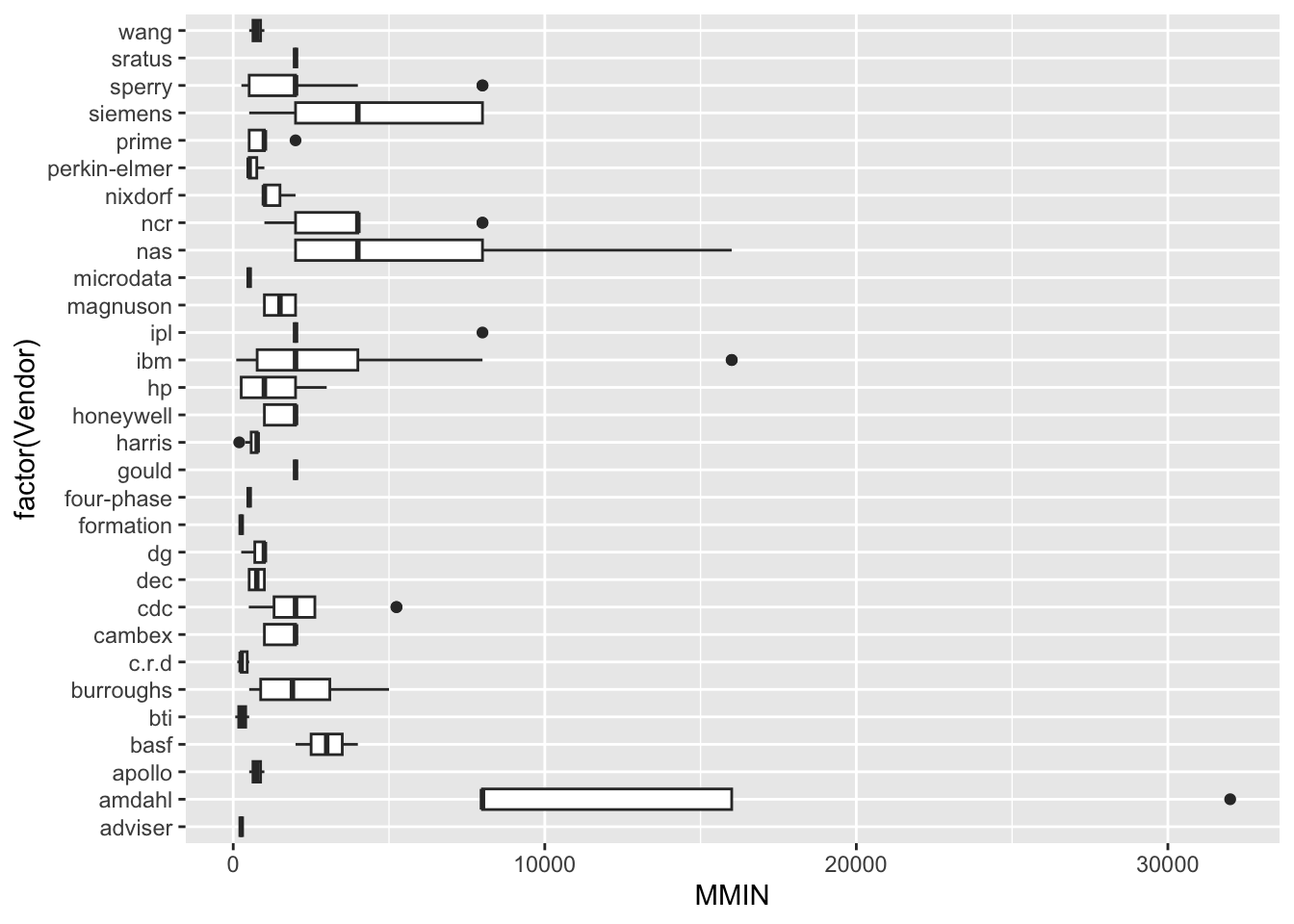
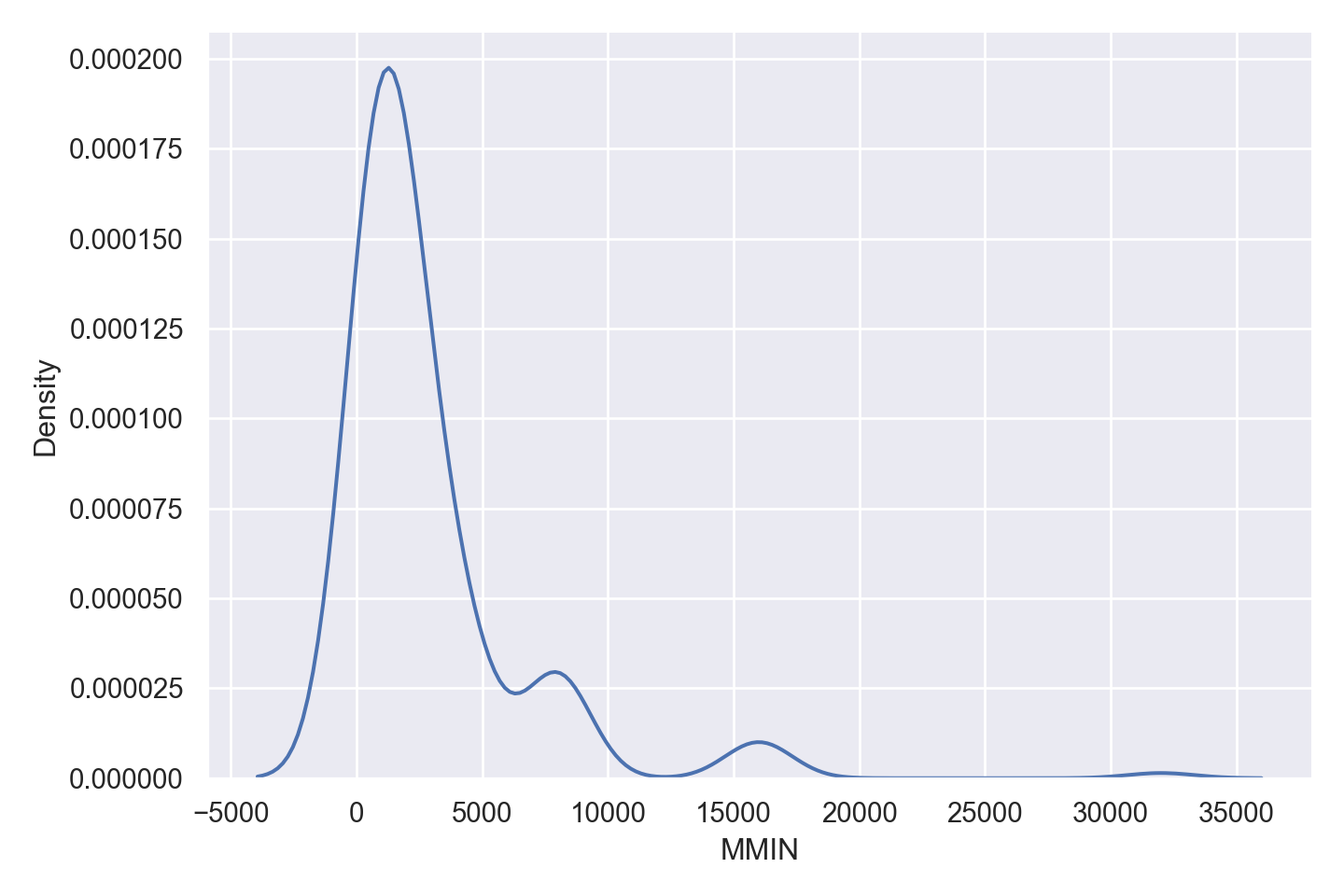
| MMIN | numeric | minimum main memory in kilobytes (integer) |
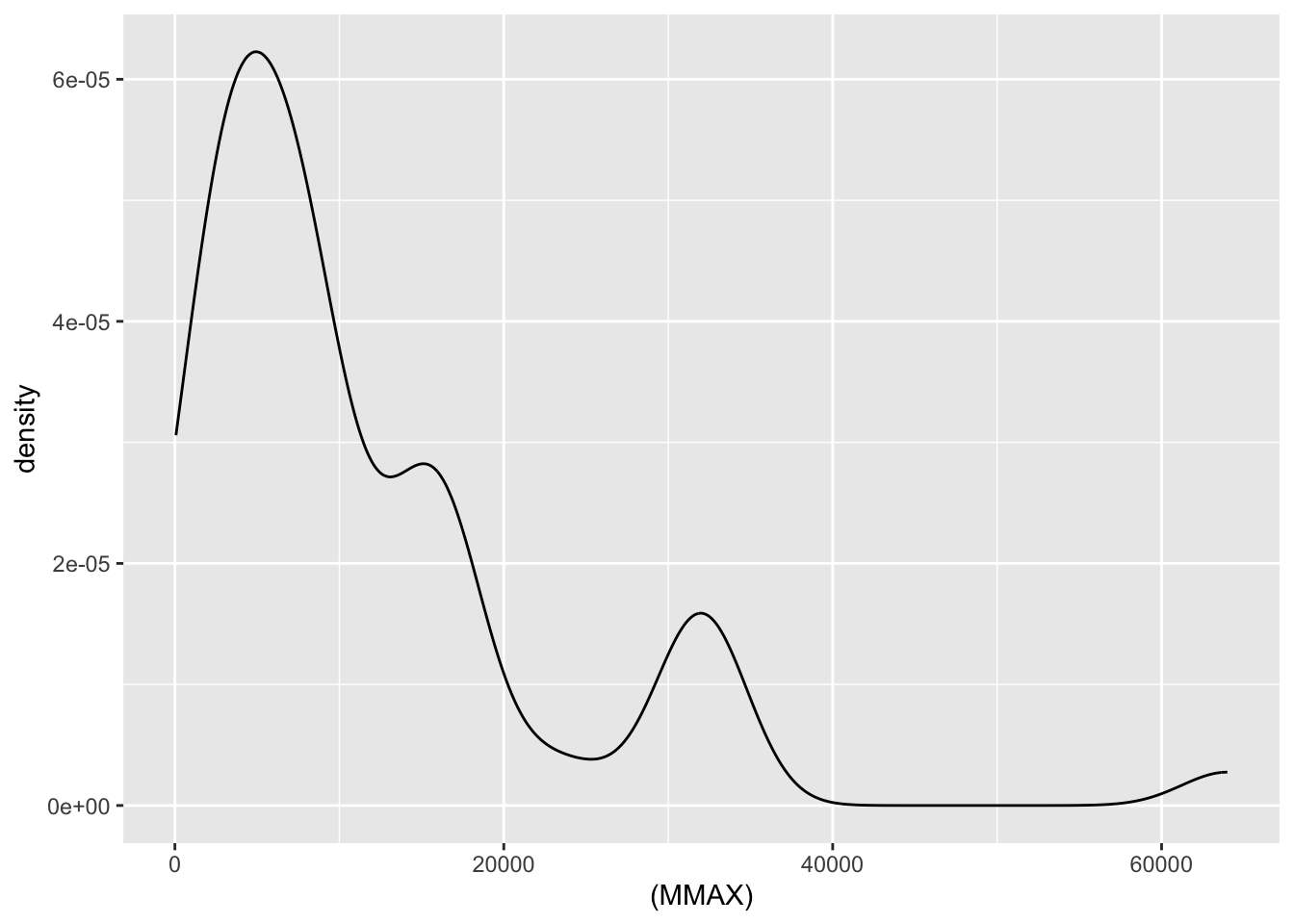
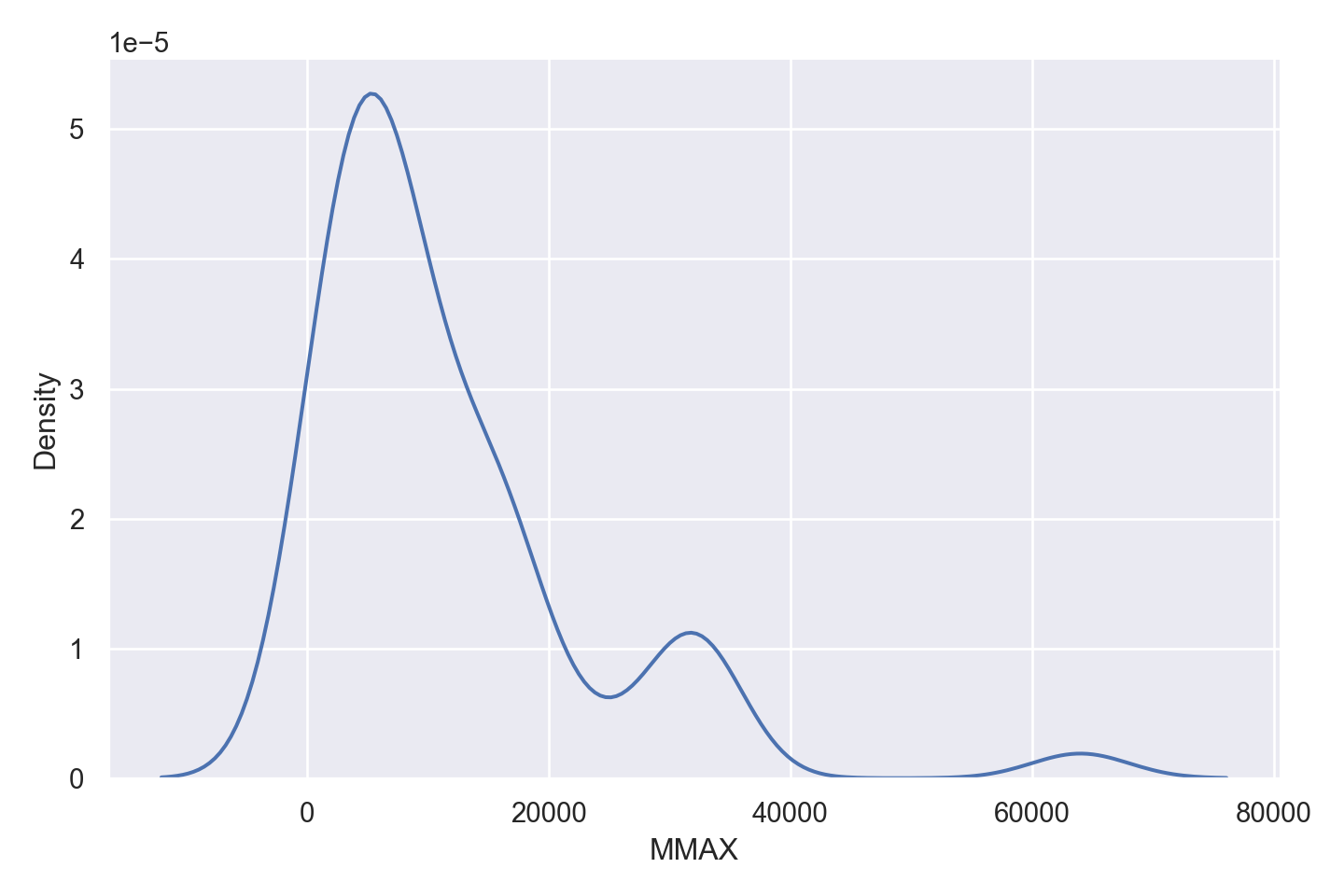
| MMAX | numeric | maximum main memory in kilobytes (integer) |
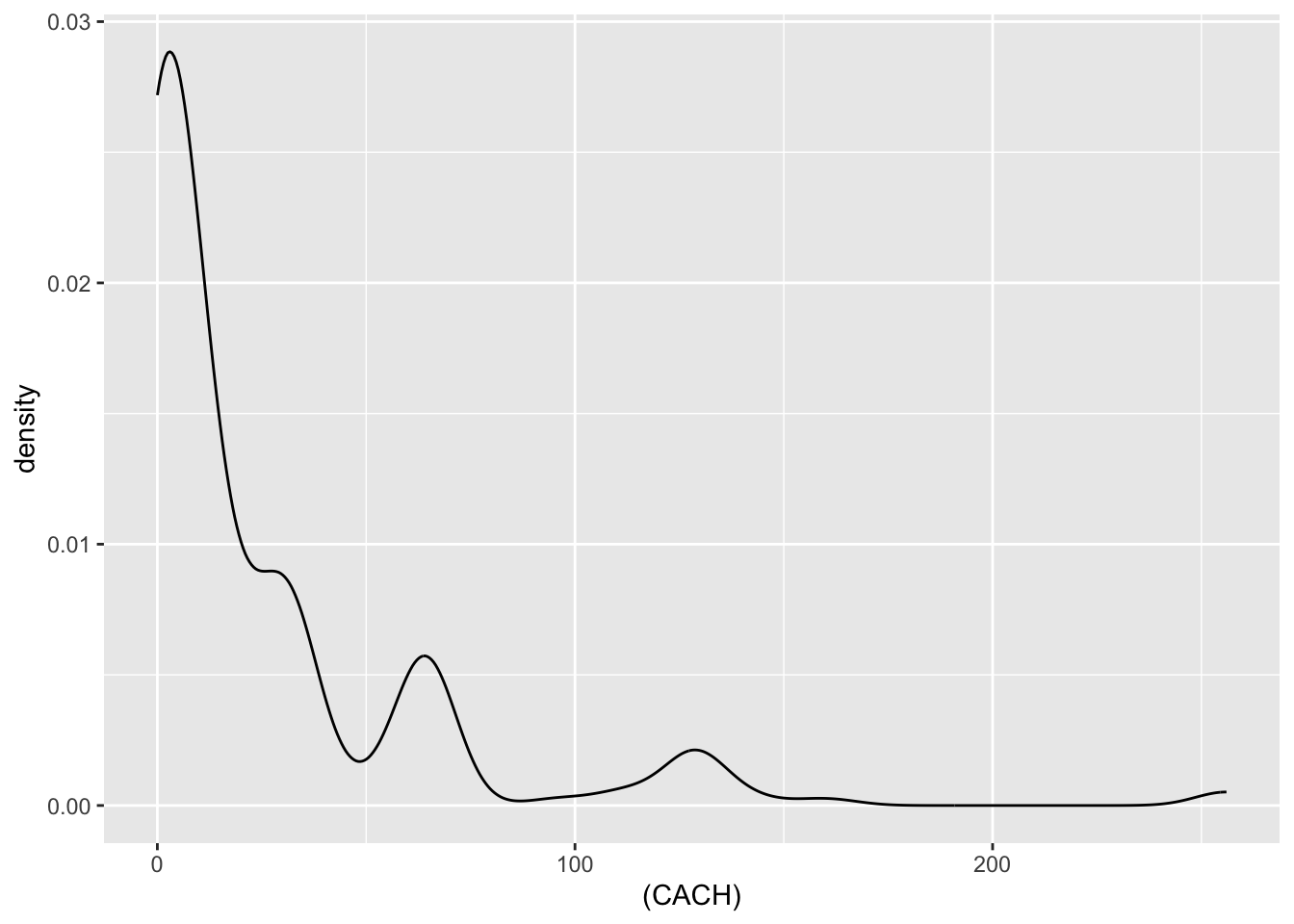
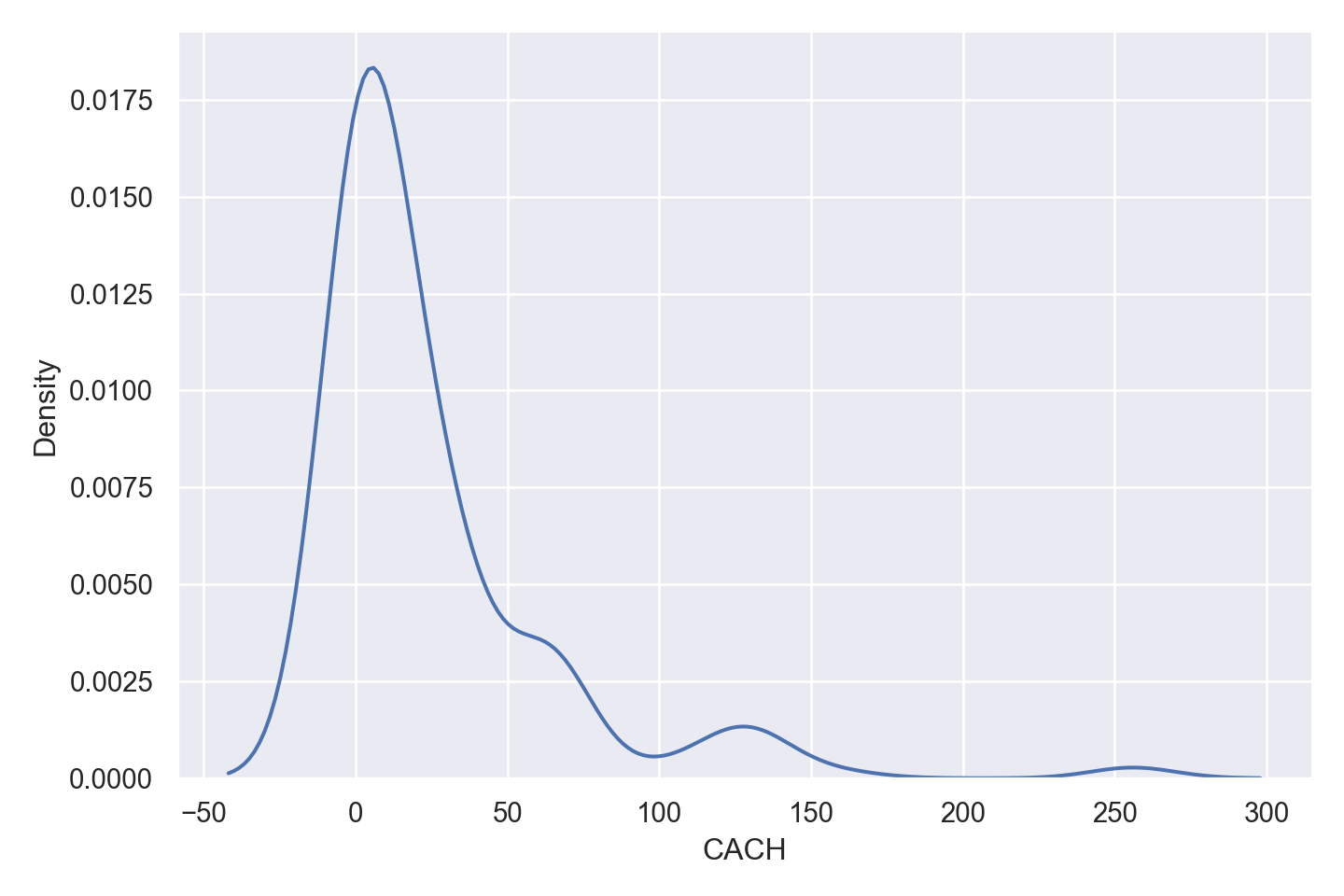
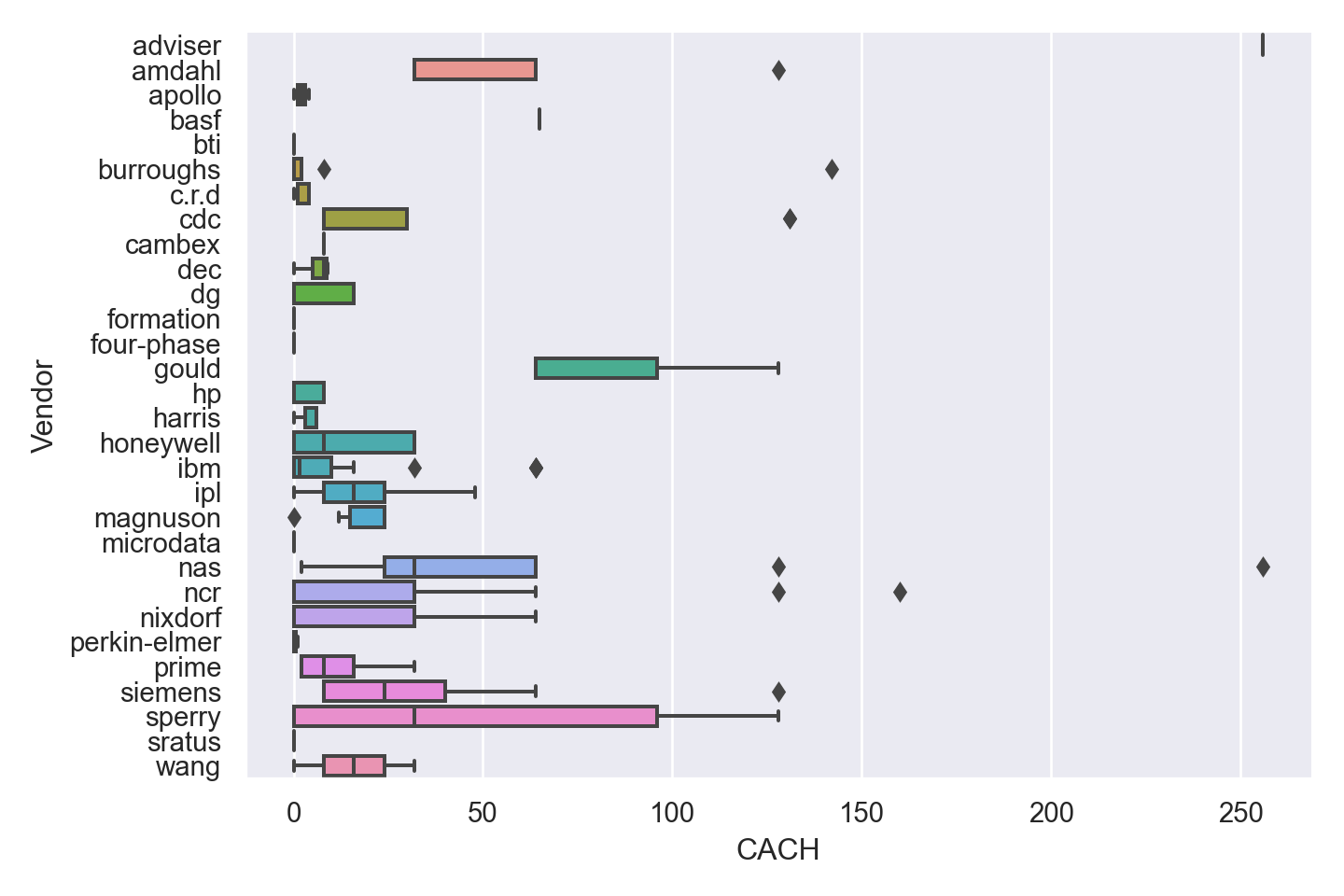
| CACH | numeric | cache memory in kilobytes (integer) |
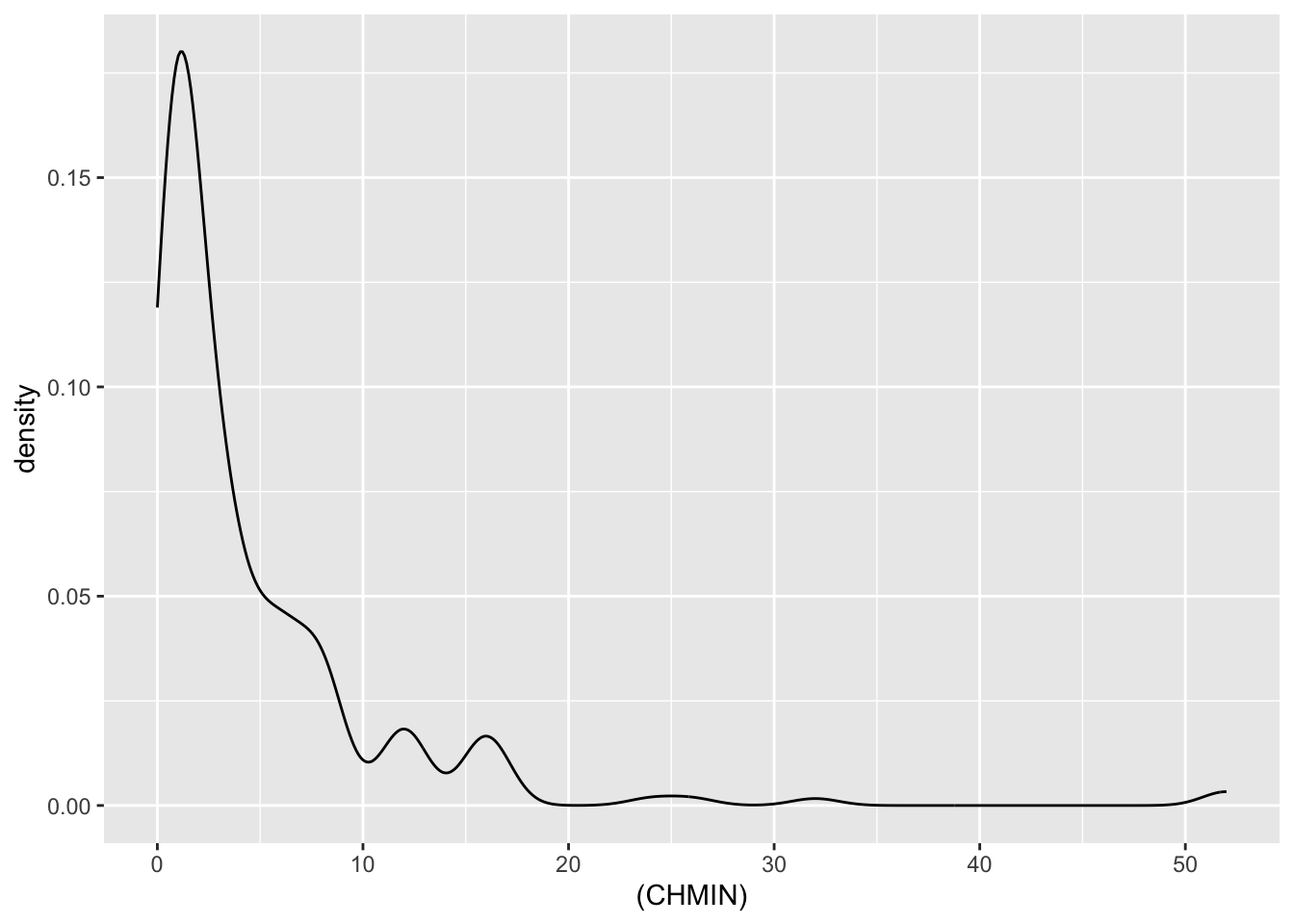
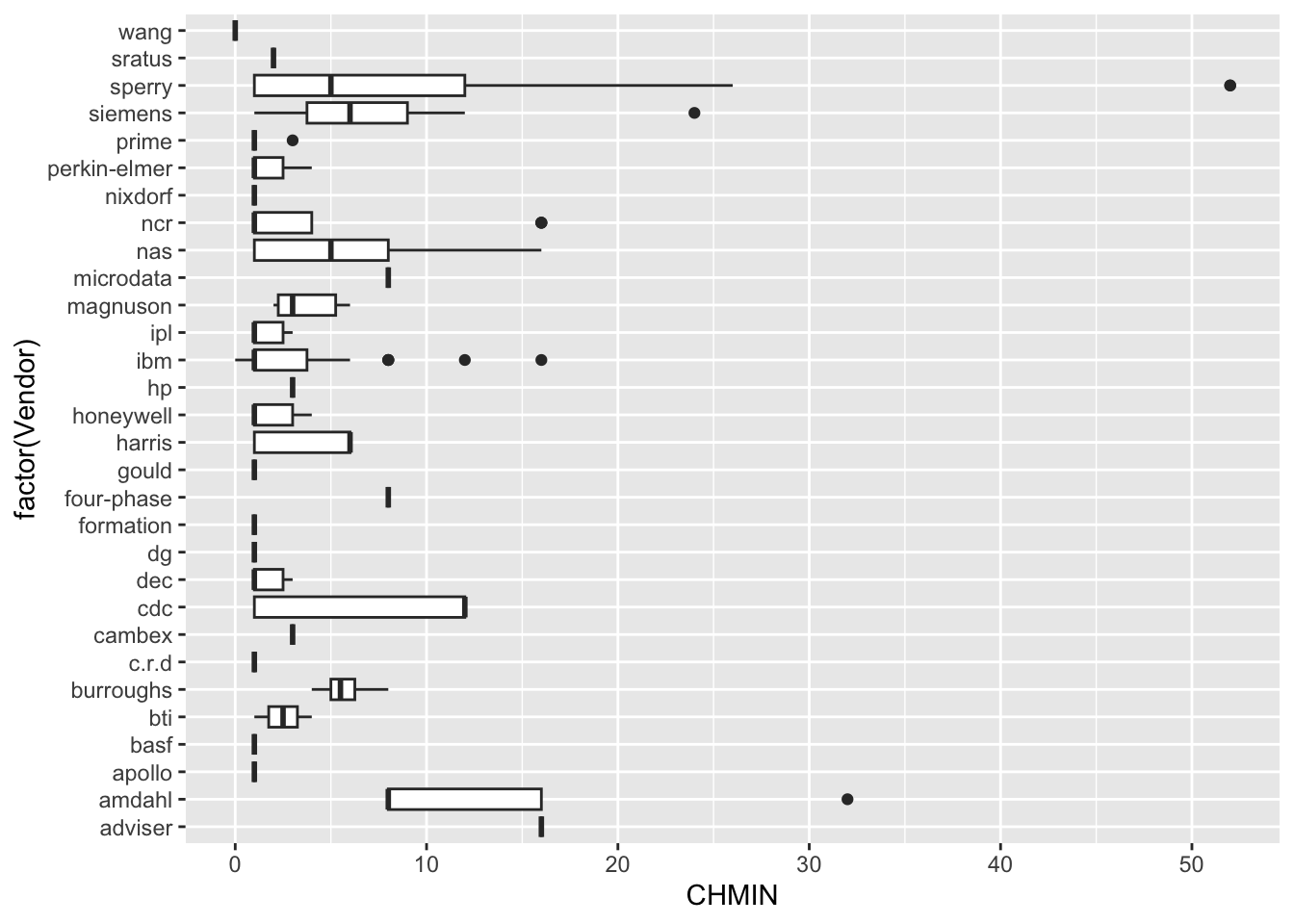
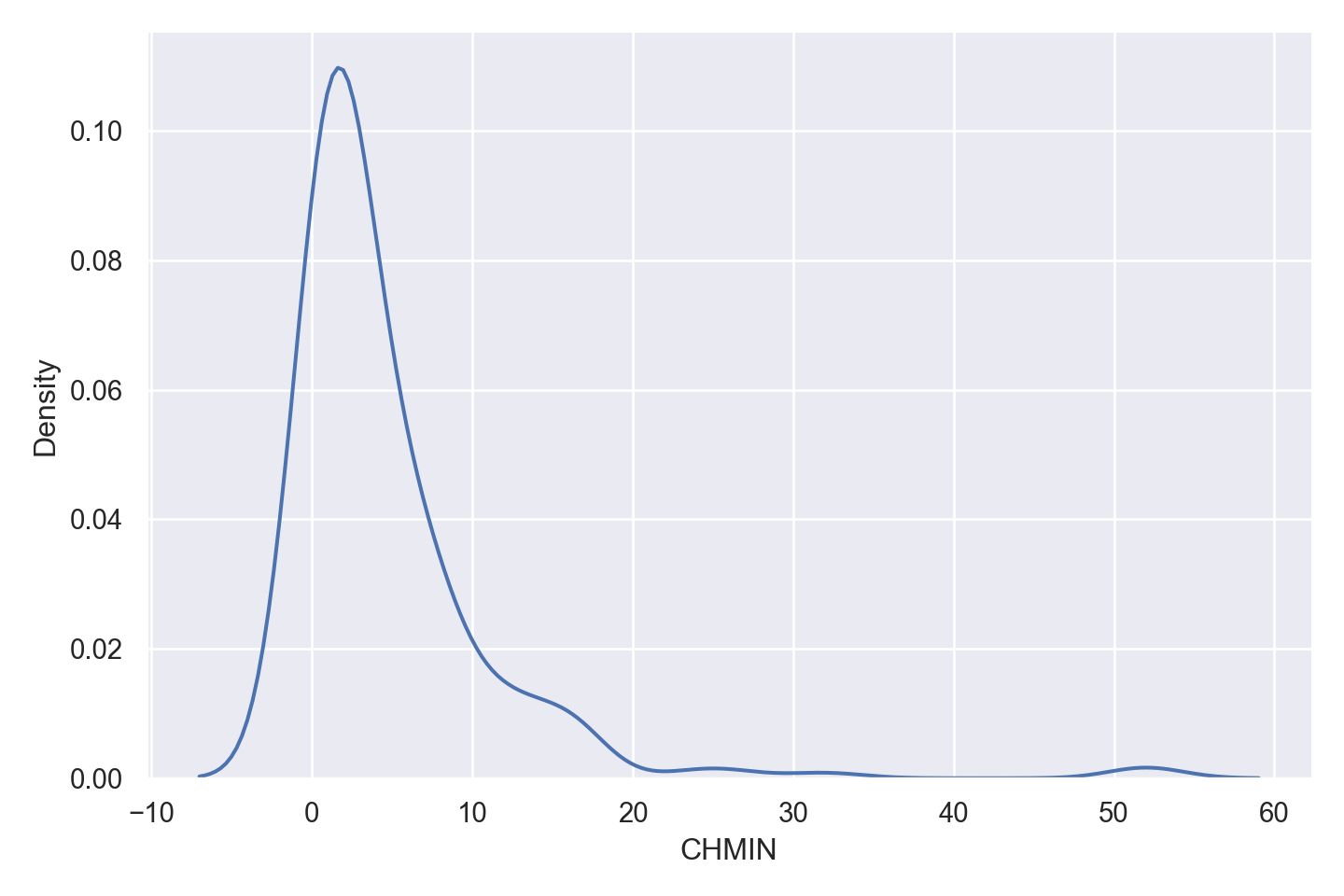
| CHMIN | numeric | minimum channels in units (integer) |
| CHMAX | numeric | maximum channels in units (integer) |
| PRP | numeric | published relative performance (integer) |
Load Packages
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import sklearn.metrics as metrics
import IPython.display as dsp
from IPython.display import HTML
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler, FunctionTransformer, PolynomialFeatures, OneHotEncoder, PowerTransformer, LabelEncoder
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline
from sklearn.pipeline import make_pipeline
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.linear_model import LogisticRegression, LogisticRegressionCV, ElasticNet, SGDClassifier, Perceptron
from sklearn.model_selection import cross_val_score, GridSearchCV, KFold, StratifiedKFold, RandomizedSearchCV
from sklearn.calibration import CalibratedClassifierCV
from sklearn.feature_selection import VarianceThreshold
from sklearn.naive_bayes import GaussianNB
from xgboost import XGBClassifier
sns.set_theme()
import warnings
warnings.filterwarnings('ignore')Load Data
data=read_csv('./data/machine.data')data = pd.read_csv("./data/machine.data", sep=",")Sample 10 rows
#knitr::kable(as_tibble(head(data_bank_marketing, n=10)))
set.seed(42)
knitr::kable(slice_sample(data, n=10))| Vendor | Model | MYCT | MMIN | MMAX | CACH | CHMIN | CHMAX | PRP | ERP |
|---|---|---|---|---|---|---|---|---|---|
| dec | vax:11/750 | 320 | 512 | 8000 | 4 | 1 | 5 | 40 | 36 |
| gould | concept:32/8750 | 75 | 2000 | 16000 | 64 | 1 | 38 | 144 | 113 |
| nas | as/8060 | 35 | 8000 | 32000 | 64 | 8 | 24 | 370 | 270 |
| harris | 100 | 300 | 768 | 3000 | 0 | 6 | 24 | 36 | 23 |
| nas | as/6620 | 60 | 2000 | 16000 | 64 | 5 | 8 | 74 | 107 |
| ibm | 4381-2 | 17 | 4000 | 16000 | 32 | 6 | 12 | 133 | 116 |
| wang | vs-90 | 480 | 1000 | 4000 | 0 | 0 | 0 | 45 | 25 |
| ipl | 4445 | 50 | 2000 | 8000 | 8 | 1 | 6 | 56 | 44 |
| dec | microvax-1 | 810 | 512 | 512 | 8 | 1 | 1 | 18 | 18 |
| burroughs | b6925 | 110 | 3100 | 6200 | 0 | 6 | 64 | 76 | 45 |
pd.set_option('display.width', 500)
#pd.set_option('precision', 3)
sample=data.sample(10)
dsp.Markdown(sample.to_markdown(index=False))| Vendor | Model | MYCT | MMIN | MMAX | CACH | CHMIN | CHMAX | PRP | ERP |
|---|---|---|---|---|---|---|---|---|---|
| harris | 600 | 300 | 768 | 4500 | 0 | 1 | 24 | 45 | 27 |
| ibm | 370/148 | 203 | 1000 | 2000 | 0 | 1 | 5 | 24 | 21 |
| microdata | seq.ms/3200 | 150 | 512 | 4000 | 0 | 8 | 128 | 30 | 33 |
| ibm | 4341-1 | 225 | 2000 | 4000 | 8 | 3 | 6 | 40 | 31 |
| honeywell | dps:7/35 | 330 | 1000 | 2000 | 0 | 1 | 2 | 16 | 20 |
| ipl | 4443 | 50 | 2000 | 8000 | 8 | 3 | 6 | 45 | 44 |
| amdahl | 580-5840 | 23 | 16000 | 32000 | 64 | 16 | 32 | 367 | 381 |
| cdc | omega:480-iii | 50 | 2000 | 8000 | 8 | 1 | 5 | 71 | 44 |
| dg | eclipse:mv/8000 | 110 | 1000 | 12000 | 16 | 1 | 2 | 60 | 56 |
| ibm | 3033:s | 57 | 4000 | 16000 | 1 | 6 | 12 | 132 | 82 |
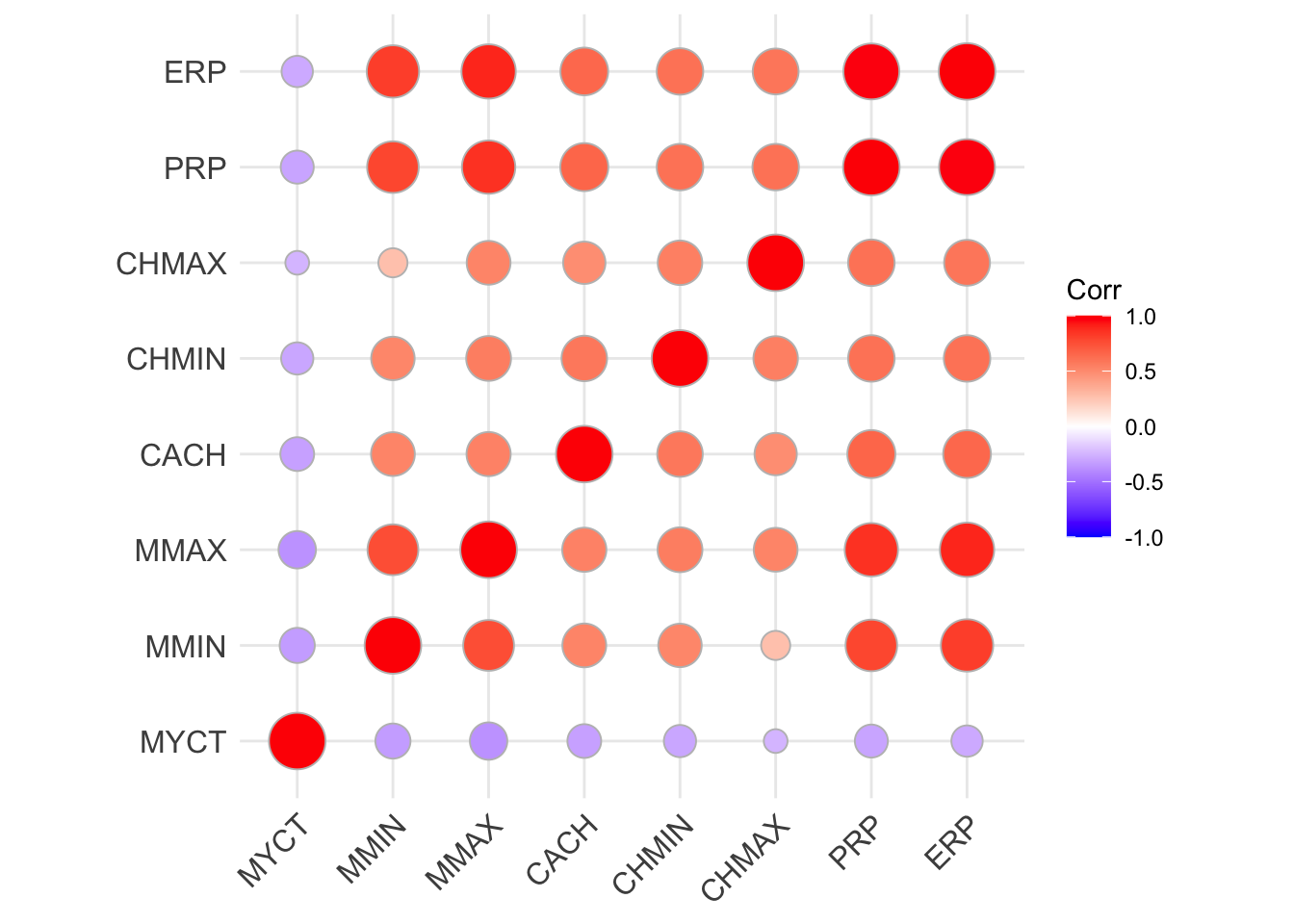
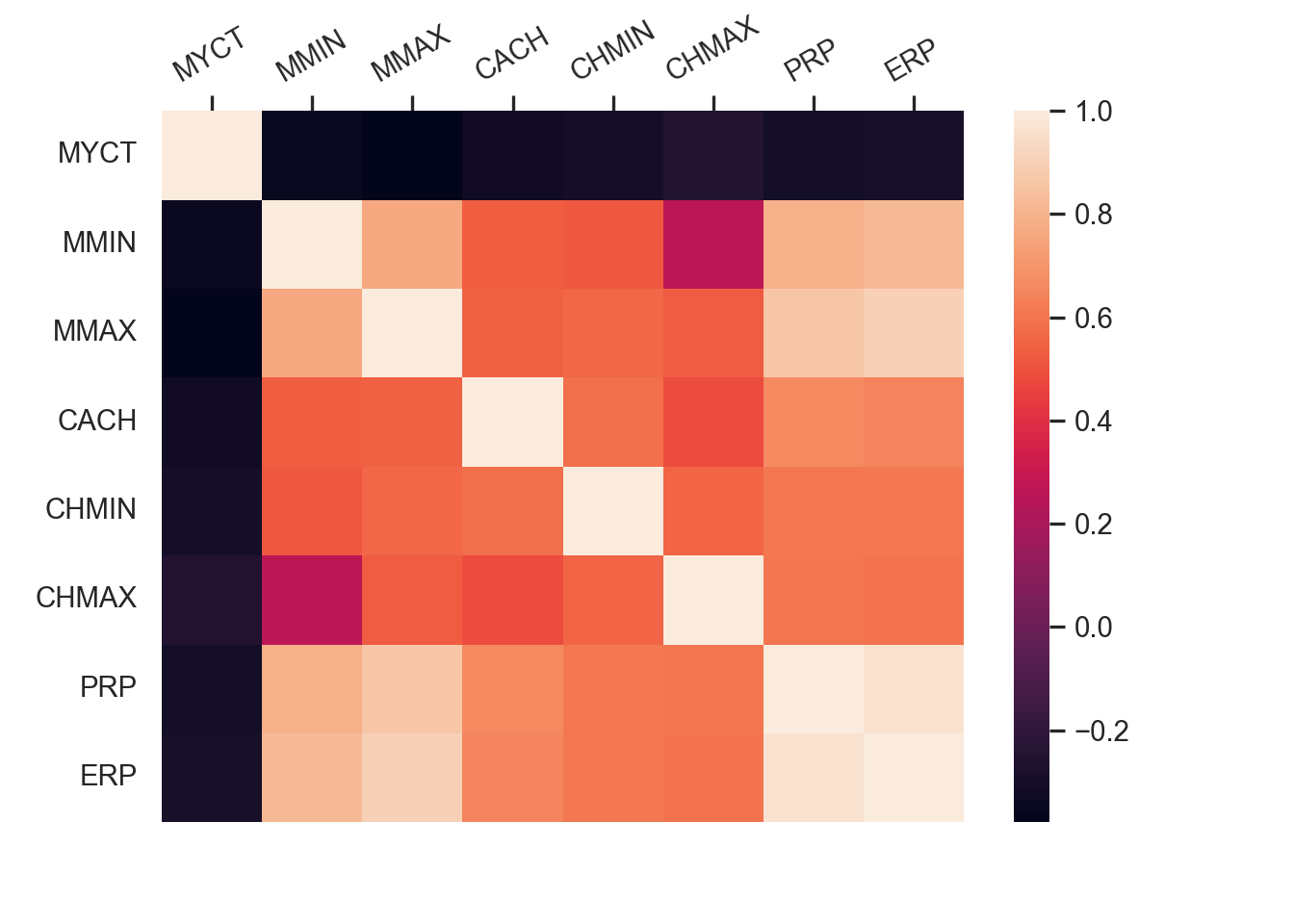
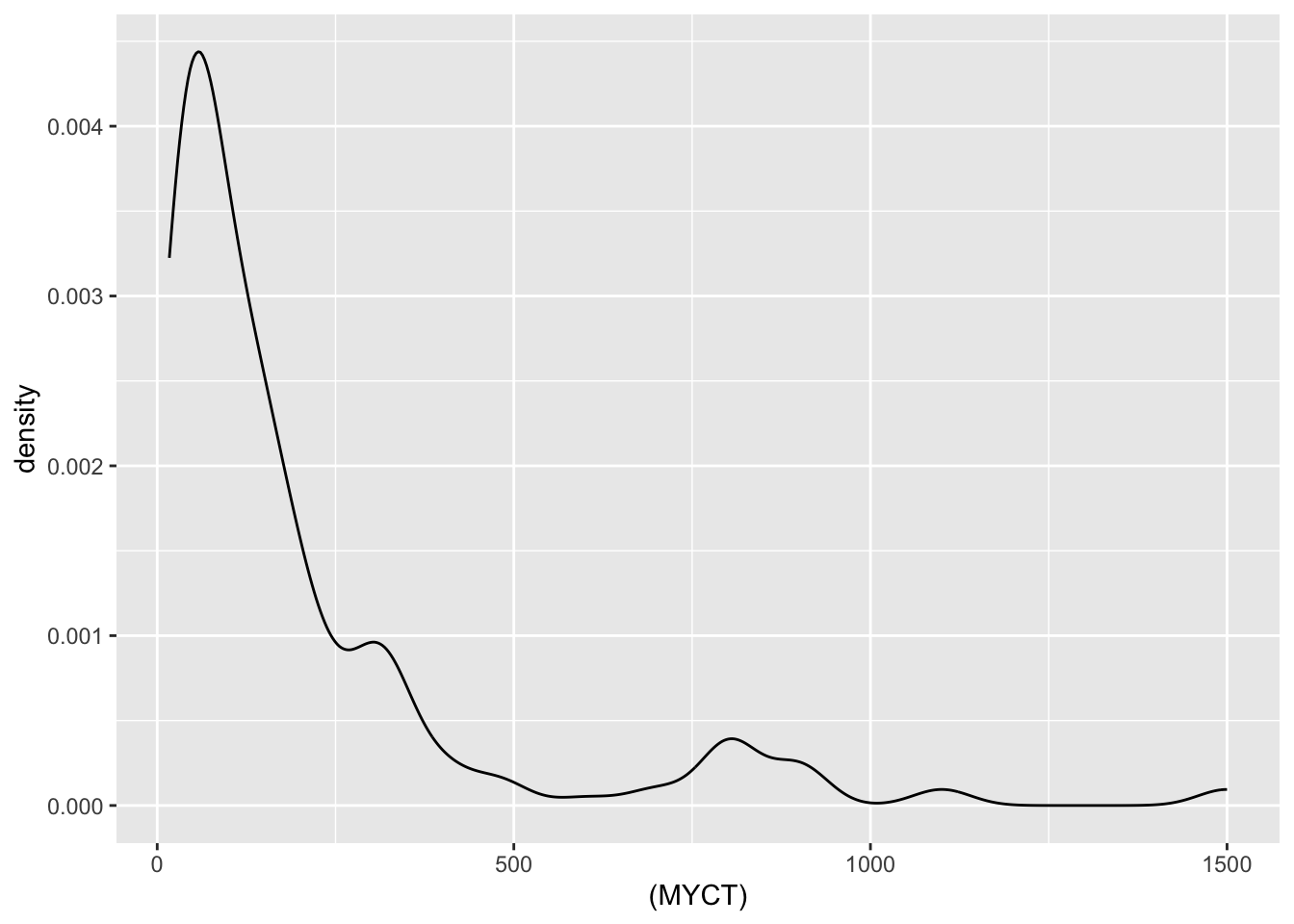
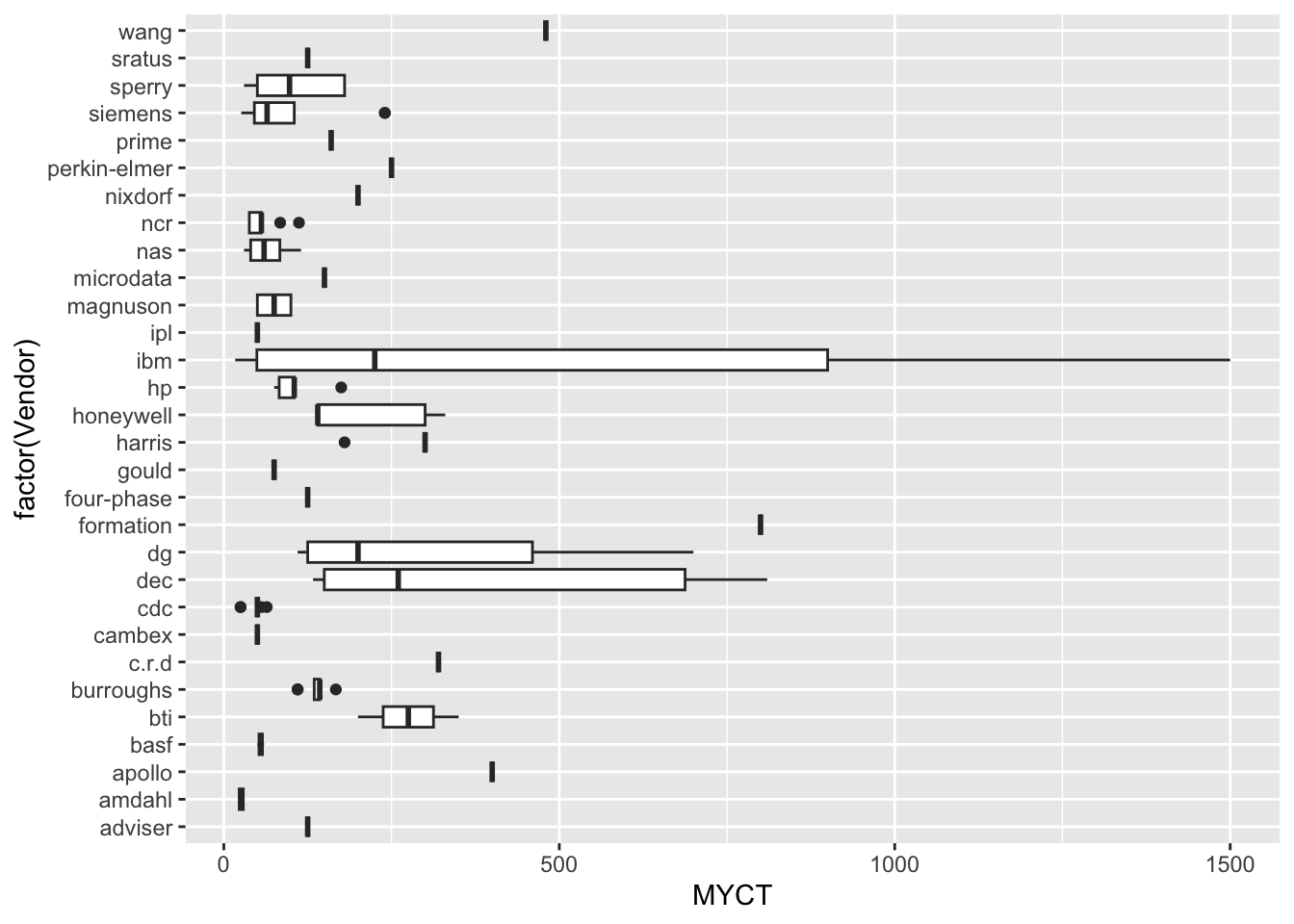
Numeric Attributes
# Model specifications
#Basic linear model
lm_basic_spec = linear_reg() %>% set_engine("lm")
#Generalized linear model with tuning
glm_spec = linear_reg(penalty = tune(), mixture = tune()) %>% set_engine("glmnet")
linear_wfs = workflow_set(
preproc = list(simple = machines_rec_1),
models = list(basic = lm_basic_spec, glm = glm_spec)
)
# Create 10 folds of the training data
data_folds = vfold_cv(data_train, strata = Vendor)
all_workflows = linear_wfs
grid_ctrl <-
control_grid(
save_pred = TRUE,
parallel_over = "everything",
save_workflow = TRUE
)
grid_results <-
linear_wfs %>%
workflow_map(
seed = 1503,
resamples = data_folds,
grid = 25,
control = grid_ctrl
)
grid_results %>% rank_results()# A tibble: 52 × 9
wflow_id .config .metric mean std_err n prepr…¹ model rank
<chr> <chr> <chr> <dbl> <dbl> <int> <chr> <chr> <int>
1 simple_basic Preprocessor1_… rmse 39.7 4.89 10 recipe line… 1
2 simple_basic Preprocessor1_… rsq 0.899 0.0254 10 recipe line… 1
3 simple_glm Preprocessor1_… rmse 45.8 9.77 10 recipe line… 2
4 simple_glm Preprocessor1_… rsq 0.886 0.0244 10 recipe line… 2
5 simple_glm Preprocessor1_… rmse 45.8 9.77 10 recipe line… 3
6 simple_glm Preprocessor1_… rsq 0.886 0.0244 10 recipe line… 3
7 simple_glm Preprocessor1_… rmse 45.8 9.77 10 recipe line… 4
8 simple_glm Preprocessor1_… rsq 0.886 0.0244 10 recipe line… 4
9 simple_glm Preprocessor1_… rmse 45.8 9.77 10 recipe line… 5
10 simple_glm Preprocessor1_… rsq 0.886 0.0244 10 recipe line… 5
# … with 42 more rows, and abbreviated variable name ¹preprocessorbest_results = grid_results %>% extract_workflow_set_result("simple_glm") %>%
select_best(metric = "rmse")
simple_glm_test_results <-
grid_results %>%
extract_workflow("simple_glm") %>%
finalize_workflow(best_results) %>%
last_fit(split = data_split)
final_fitted_model = simple_glm_test_results %>% extract_fit_parsnip()
simple_glm_test_results %>% collect_predictions() %>% arrange(.row)# A tibble: 53 × 5
id .pred .row PRP .config
<chr> <dbl> <int> <dbl> <chr>
1 train/test split 979. 10 1144 Preprocessor1_Model1
2 train/test split -31.9 15 10 Preprocessor1_Model1
3 train/test split 364. 20 120 Preprocessor1_Model1
4 train/test split 43.1 21 30 Preprocessor1_Model1
5 train/test split 32.0 25 23 Preprocessor1_Model1
6 train/test split 23.2 26 69 Preprocessor1_Model1
7 train/test split 35.1 29 77 Preprocessor1_Model1
8 train/test split 124. 32 368 Preprocessor1_Model1
9 train/test split 195. 35 106 Preprocessor1_Model1
10 train/test split 89.1 39 71 Preprocessor1_Model1
# … with 43 more rowssimple_linear_model_metrics = collect_metrics(simple_glm_test_results)
simple_linear_model_metrics# A tibble: 2 × 4
.metric .estimator .estimate .config
<chr> <chr> <dbl> <chr>
1 rmse standard 66.2 Preprocessor1_Model1
2 rsq standard 0.924 Preprocessor1_Model1# Find the metrics of existing estimated results
estimated_rmse=rmse(data_test, truth = PRP, estimate = ERP)
estimated_rsq=rsq(data_test, truth = PRP, estimate = ERP)
boxinvTransform <- function(y, lambda=-0.219) {
if (lambda == 0L) { exp(y) }
else { (y * lambda + 1)^(1/lambda) }
}
pred= as.tibble(simple_glm_test_results$.predictions[[1]]$.pred)
PRP = as.tibble(simple_glm_test_results$.predictions[[1]]$PRP)
#define plotting area
#op <- par(pty = "s", mfrow = c(1, 2))
#Q-Q plot for original model
#qqnorm(model$residuals)
#qqline(model$residuals)
#Q-Q plot for Box-Cox transformed model
#qqnorm(new_model$residuals)
#qqline(new_model$residuals)
#display both Q-Q plots
#par(op)
# Define the basic pre-processing recipe. This one does not have any predictor transformations or interactions.
machines_rec_2 = recipe(PRP ~ ., data = data_train) %>%
step_novel(all_predictors(), -all_numeric()) %>%
step_rm(ERP) %>%
update_role(Model, new_role = "ID") %>%
step_dummy(all_predictors(), -all_numeric())
decision_tree_spec = decision_tree(tree_depth = 5) %>% set_engine("rpart") %>% set_mode("regression")
boost_tree_spec = boost_tree(trees = 10) %>% set_engine("xgboost") %>% set_mode("regression")
rand_forest_spec = rand_forest(trees = 1000, mtry = tune()) %>% set_engine("randomForest") %>% set_mode("regression")
tree_wfs = workflow_set(
preproc = list(simple = machines_rec_2),
models = list(decision_tree = decision_tree_spec, boost_tree = boost_tree_spec, rand_forest = rand_forest_spec)
)
grid_results <-
tree_wfs %>%
workflow_map(
seed = 1503,
resamples = data_folds,
grid = 25,
control = grid_ctrl
)
grid_results %>% rank_results()# A tibble: 52 × 9
wflow_id .config .metric mean std_err n prepr…¹ model rank
<chr> <chr> <chr> <dbl> <dbl> <int> <chr> <chr> <int>
1 simple_rand_forest Preproce… rmse 44.3 12.5 10 recipe rand… 1
2 simple_rand_forest Preproce… rsq 0.863 0.0439 10 recipe rand… 1
3 simple_rand_forest Preproce… rmse 44.5 12.6 10 recipe rand… 2
4 simple_rand_forest Preproce… rsq 0.862 0.0438 10 recipe rand… 2
5 simple_rand_forest Preproce… rmse 44.5 12.5 10 recipe rand… 3
6 simple_rand_forest Preproce… rsq 0.862 0.0430 10 recipe rand… 3
7 simple_rand_forest Preproce… rmse 44.5 12.5 10 recipe rand… 4
8 simple_rand_forest Preproce… rsq 0.861 0.0437 10 recipe rand… 4
9 simple_rand_forest Preproce… rmse 44.6 12.7 10 recipe rand… 5
10 simple_rand_forest Preproce… rsq 0.861 0.0434 10 recipe rand… 5
# … with 42 more rows, and abbreviated variable name ¹preprocessorbest_results = grid_results %>% extract_workflow_set_result("simple_rand_forest") %>%
select_best(metric = "rmse")
simple_rf_test_results <-
grid_results %>%
extract_workflow("simple_rand_forest") %>%
finalize_workflow(best_results) %>%
last_fit(split = data_split)
final_fitted_rf_model = simple_rf_test_results %>% extract_fit_parsnip()
simple_rf_test_results %>% collect_predictions()# A tibble: 53 × 5
id .pred .row PRP .config
<chr> <dbl> <int> <dbl> <chr>
1 train/test split 631. 10 1144 Preprocessor1_Model1
2 train/test split 16.7 15 10 Preprocessor1_Model1
3 train/test split 175. 20 120 Preprocessor1_Model1
4 train/test split 45.0 21 30 Preprocessor1_Model1
5 train/test split 35.0 25 23 Preprocessor1_Model1
6 train/test split 19.8 26 69 Preprocessor1_Model1
7 train/test split 27.4 29 77 Preprocessor1_Model1
8 train/test split 217. 32 368 Preprocessor1_Model1
9 train/test split 180. 35 106 Preprocessor1_Model1
10 train/test split 46.9 39 71 Preprocessor1_Model1
# … with 43 more rowssimple_rf_model_metrics = collect_metrics(simple_rf_test_results)
simple_rf_model_metrics# A tibble: 2 × 4
.metric .estimator .estimate .config
<chr> <chr> <dbl> <chr>
1 rmse standard 104. Preprocessor1_Model1
2 rsq standard 0.906 Preprocessor1_Model1machines_rec_norm = machines_rec_2
mlp_spec = mlp() %>% set_engine("nnet") %>% set_mode("regression")
svm_spec = svm_rbf() %>% set_engine("kernlab") %>% set_mode("regression")
rule_spec = rule_fit(trees = 1000) %>% set_engine("h2o") %>% set_mode("regression")
normalized_wfs = workflow_set(
preproc = list(simple = machines_rec_norm),
models = list(mlp = mlp_spec, svm = svm_spec)
)
grid_results <-
normalized_wfs %>%
workflow_map(
seed = 1503,
resamples = data_folds,
grid = 25,
control = grid_ctrl
)
grid_results %>% rank_results()# A tibble: 4 × 9
wflow_id .config .metric mean std_err n prepr…¹ model rank
<chr> <chr> <chr> <dbl> <dbl> <int> <chr> <chr> <int>
1 simple_mlp Preprocessor1_Mo… rmse 120. 17.1 10 recipe mlp 1
2 simple_mlp Preprocessor1_Mo… rsq 0.119 0.0442 2 recipe mlp 1
3 simple_svm Preprocessor1_Mo… rmse 121. 21.1 10 recipe svm_… 2
4 simple_svm Preprocessor1_Mo… rsq 0.333 0.0532 10 recipe svm_… 2
# … with abbreviated variable name ¹preprocessorbest_results = grid_results %>% extract_workflow_set_result("simple_mlp") %>%
select_best(metric = "rmse")
simple_mlp_test_results <-
grid_results %>%
extract_workflow("simple_mlp") %>%
finalize_workflow(best_results) %>%
last_fit(split = data_split)
final_fitted_mlp_model = simple_mlp_test_results %>% extract_fit_parsnip()
simple_mlp_test_results %>% collect_predictions()# A tibble: 53 × 5
id .pred .row PRP .config
<chr> <dbl> <int> <dbl> <chr>
1 train/test split 97.8 10 1144 Preprocessor1_Model1
2 train/test split 15.0 15 10 Preprocessor1_Model1
3 train/test split 97.8 20 120 Preprocessor1_Model1
4 train/test split 97.8 21 30 Preprocessor1_Model1
5 train/test split 97.8 25 23 Preprocessor1_Model1
6 train/test split 97.8 26 69 Preprocessor1_Model1
7 train/test split 97.8 29 77 Preprocessor1_Model1
8 train/test split 97.8 32 368 Preprocessor1_Model1
9 train/test split 97.8 35 106 Preprocessor1_Model1
10 train/test split 97.8 39 71 Preprocessor1_Model1
# … with 43 more rowssimple_mlp_model_metrics = collect_metrics(simple_rf_test_results)
simple_mlp_model_metrics# A tibble: 2 × 4
.metric .estimator .estimate .config
<chr> <chr> <dbl> <chr>
1 rmse standard 104. Preprocessor1_Model1
2 rsq standard 0.906 Preprocessor1_Model1The GLM model without any interaction terms gives the best results with RMSE = 66.22 and R-squared = 0.9235.